相関分析について

この記事では相関分析について、初心者の方向けに詳しく解説します。

ここで、まず量的データについて解説します。

枚数、身長、金額など、数値で推し測ることができ、数字の大小に意味をもつデータです。 人数、回数など、整数として表現されるデータで、一般的に連続して測ることができないデータ例）人数を数える時、1人の次は一般的に２人であり、1.00……001人とは数えない。

» データ・データセットの種類-総務省統計局より引用

ここで量的データの分析は、以下のように大きくは2つに分けることができます。

1つが「差の検定」と呼ばれるものです。

差の検定には、2つの条件あるいは群の間に差があるかを調べる t 検定や、3つ以上の条件群の間に差があるかを調べる分散分析が含まれます。

もう1つが「関係の検定」と呼ばれるものです。

関係の検定には、この記事で説明する相関分析や、別の講座で説明する回帰分析が含まれます。

$t$ 検定や分散分析では、1種類多くても3種類の独立変数が従属変数に及ぼす影響しか検討できません。

ところが、相関分析ではたくさんの変数同士の関連を一度に明らかにすることができます。

そのため、たくさんの変数を扱う調査では相関分析は非常に便利です。

この記事では、まず「相関」とは何かについて丁寧に説明したうえで、偏相関分析や層別解析といった応用的な相関分析について説明していきます。

この記事では相関分析の計算の仕方は割愛しますが、まずは相関分析の考え方をしっかり理解しましょう。

また、記事の前に相関分析についても有益な動画ありましたのでご参照ください。（少し回帰の内容も入っています。）

相関とは、ある変数 $x$ が一方向に変化するにつれて、別の変数 $y$ も一方向に変化するといった関係のことです。

例えば、塩分は血圧を高めるので、1日あたりの塩分摂取量（変数 $x$ ）が多いほど最高血圧(変数 $y$ )が高くなります。

逆に、運動には血圧を下げる効果があるので、1週間あたりの運動時間（変数 $x$ ）が長いほど最高血圧(変数 $y$ )は低くなります。

相関を一般的な言葉で表現すると比例の関係や反比例の関係と言えるでしょう。

相関とは|散布図から見えてくるデータ同士の関係

「記述統計のグラフ」の記事で詳しく解説していますが、相関は散布図というグラフで視覚化することができます。
» 記述統計のグラフについて【データの特徴やグラフの見方】

散布図とは、ある変数 $x$ を縦軸に、別の変数 $y$ を横軸にして、それぞれの軸の目盛を元にデータを点で表したグラフです。

先ほどの1日あたりの塩分摂取量（変数 $x$ ）と最高血圧（変数 $y$ ）についての架空のデータの散布図は、以下のようになります。

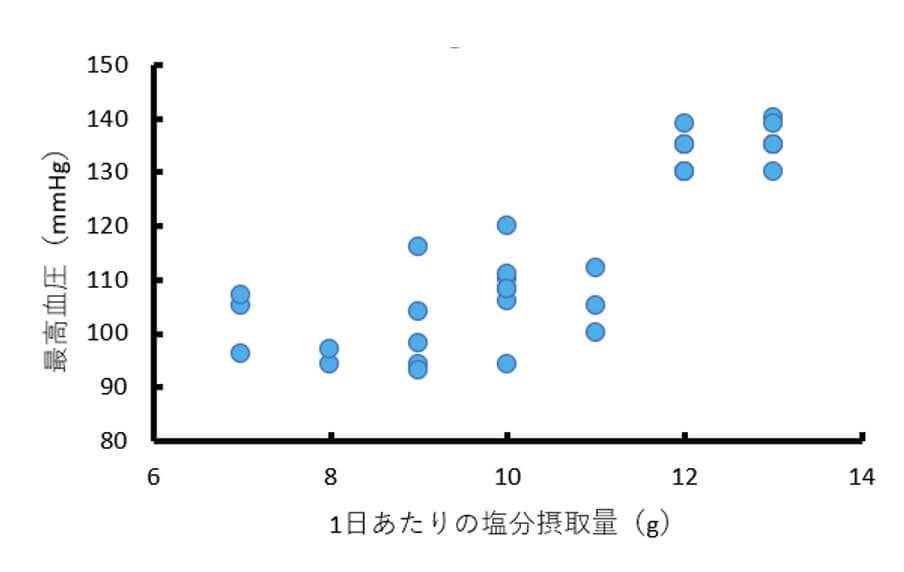散布図を見ていると、何となく比例の直線関係が見えてくる気がします。笑

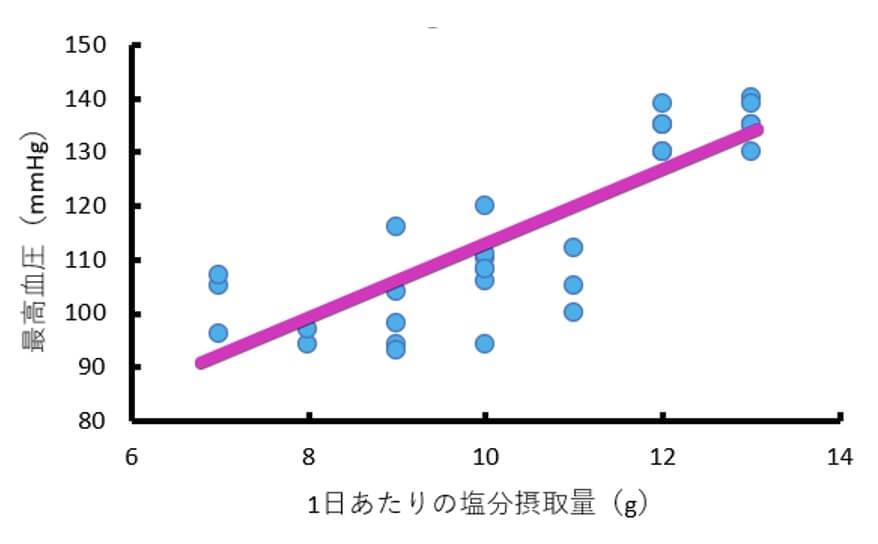
このようにデータを散布図で表現することで2種類のデータに相関がありそうか分かります。

相関の種類|正の相関、負の相関、無相関について

「相関とは|散布図から見えてくるデータ同士の関係」では、相関のことを比例関係や反比例関係と表現しました。

しかし、一般的に統計学では比例関係や反比例関係という表現はしません。

統計学（統計の多くの教科書）では、比例関係を「正の相関」、反比例関係を「負の相関」と呼ばれる事が多いです。

先ほどの「1日あたりの塩分摂取量と最高血圧には比例関係がある」を統計学的に表現すると、「1日あたりの塩分摂取量と最高血圧の間には正の相関がある」となります。

正の相関の散布図は、以下のように右上がりの形です。

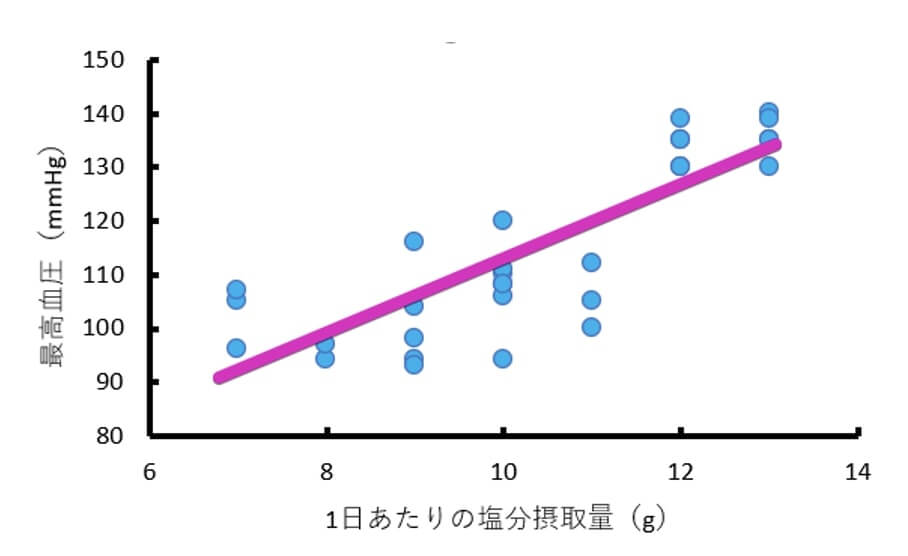
また、「1週間あたりの運動時間と最高血圧には反比例関係がある」を統計学的に表現すると「1週間あたりの運動時間と最高血圧の間には負の相関がある」となります。

負の相関の散布図は、以下のように右下がりの形です。
※1週間あたりの運動時間と最高血圧のデータは架空データです。

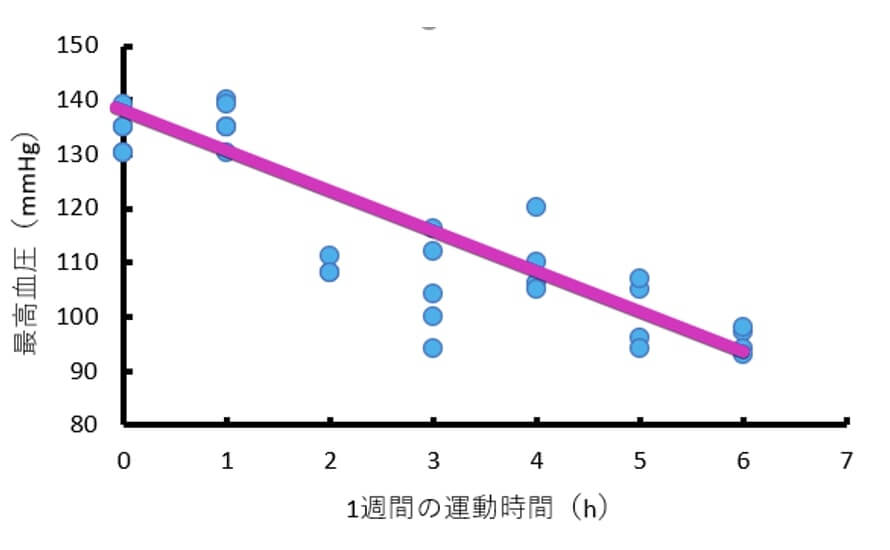
なお、2つの変数の間に全く関係がないこともあります。

その場合は「無相関」という用語で表現され、「2つの変数の間には相関はない」ということになります。

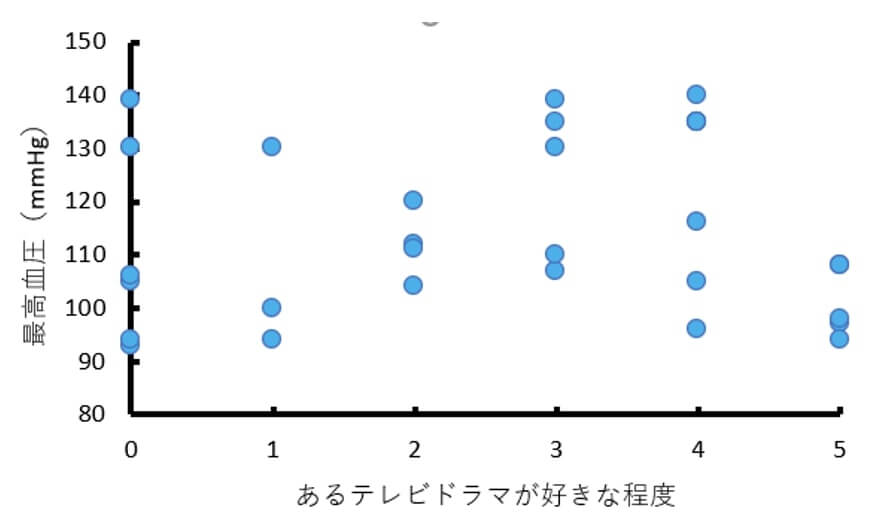
例えば、あるテレビドラマを好きな程度と、最高血圧との間には関連がないと考えるのは自然ですよね。

これを散布図で表現すると、以下のように散らばった分布になります。

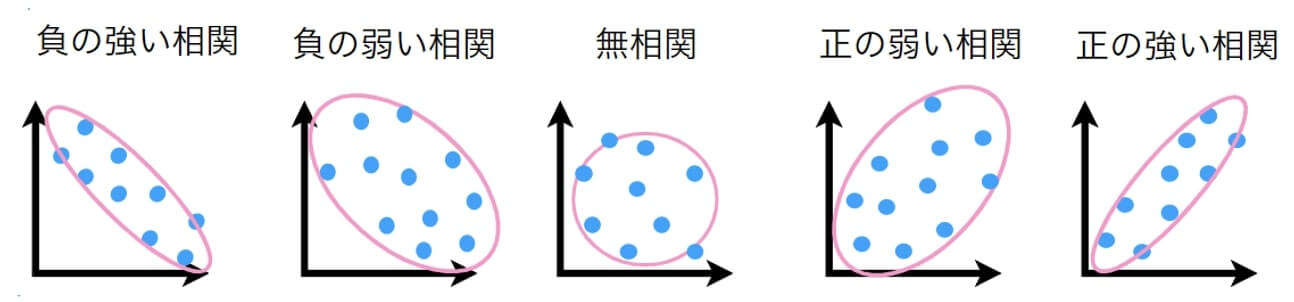
相関には符号（正・負）だけではなく、強さ（強い・弱い）という形容詞が伴います。

$0$ は無相関で、$＋1$ に近づくほど正の強い相関、$-1$ に近づくほど負の強い相関となります。

相関の注意点

片方の変数について高群・低群に分けてもう一つの変数を従属変数とする $t$ 検定を行っても、相関分析と同じように「ある変数の得点が高いともう一つの変数の得点が高い（あるいは低い）」という結果を出すことはできます。

しかし、$t$ 検定を繰り返すと第一種の過誤を引き起こしやすくなるため、本当は関連がない変数同士に「関連がある」と誤った判断をしてしまう恐れがあります。

一方で、統計処理ソフトで相関分析を行えば、たくさんの変数同士の関連を一度に明らかにすることができます。（個人的にはR推奨しています。）

そのため、多くの変数同士の関連を見たいというときには相関分析は非常に便利です。

しかし、相関分析で明らかにされる相関も万能ではありません。

注意すべき点が以下3つあります。

相関関係と因果関係とは【相関関係と因果関係のの違いについて】

まず、相関関係と因果関係は別物だということに注意しておく必要があります。

相関関係と因果関係の定義は以下の通りです。

因果関係は「因果」という関連に限定しているため、因果関係は相関関係の一つと言うことができます。

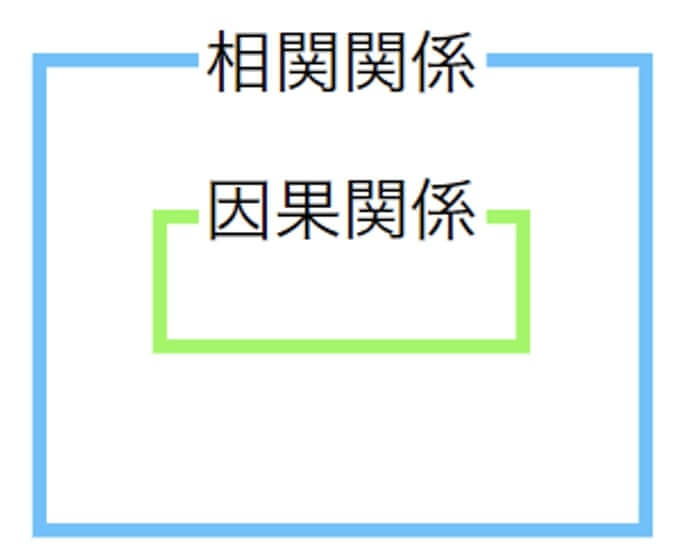
負の相関の例として、1週間あたりの運動時間と最高血圧の関係を考えました。

この2つの変数の関係は相関関係でしょうか？それとも因果関係でしょうか。

もしこれが調査データを元に得た統計結果だとしたら、1週間あたりの運動時間と最高血圧との間には因果関係があると言ってしまうのは早計だと言えます。

それというのも、運動しているから最高血圧が低い健康な状態でいられるというように「1週間あたりの運動時間→最高血圧」という因果関係が考えられると同時に、最高血圧が高くて危険だからあまり運動しないようにしているとしている高血圧の方もいるように「最高血圧→1週間あたりの運動時間」という因果関係も考えられるからです。

もし、「1週間あたりの運動時間→最高血圧」という因果関係を明らかにしようとするならば、例えば以下のような実験を行う必要があります。

調査は実験と異なり、多くの場合時間軸において全てのデータが同じ土俵にあります。

逆の方向性も考えられる以上、相関が認められたとしても因果関係があると言う表現は控えたほうがよいでしょう。

とはいえ、調査で得たデータの変数同士の関係が因果関係と言える場合もあります。

例えば、各都道府県の成人喫煙率とがんの肺がんの人口10万対罹患率との間には正の相関が認められると思います。

タバコを吸うから肺がんになるということはあっても、肺がんになったからわざわざタバコを吸うようになるということはありませんよね。

そのため、調査だから因果関係を絶対に明らかにできないということはないです。

擬似相関について｜本来は関連のないデータ同士に相関が見えることがある

相関分析によって相関が認められるからといっても、それが正しいものであるとは限りません。

おそらく誰も研究していないテーマなのでデータはありませんが、最高血圧の高さと年賀状を出す枚数との間には正の相関が認められるはずです。

論理的に考えてみると、おかしいですよね。

しかし、これには以下のカラクリがあります。

つまり、年齢という共通要因が働いていて、最高血圧の高さと年賀状を出す枚数との間に正の相関が認められるのです。

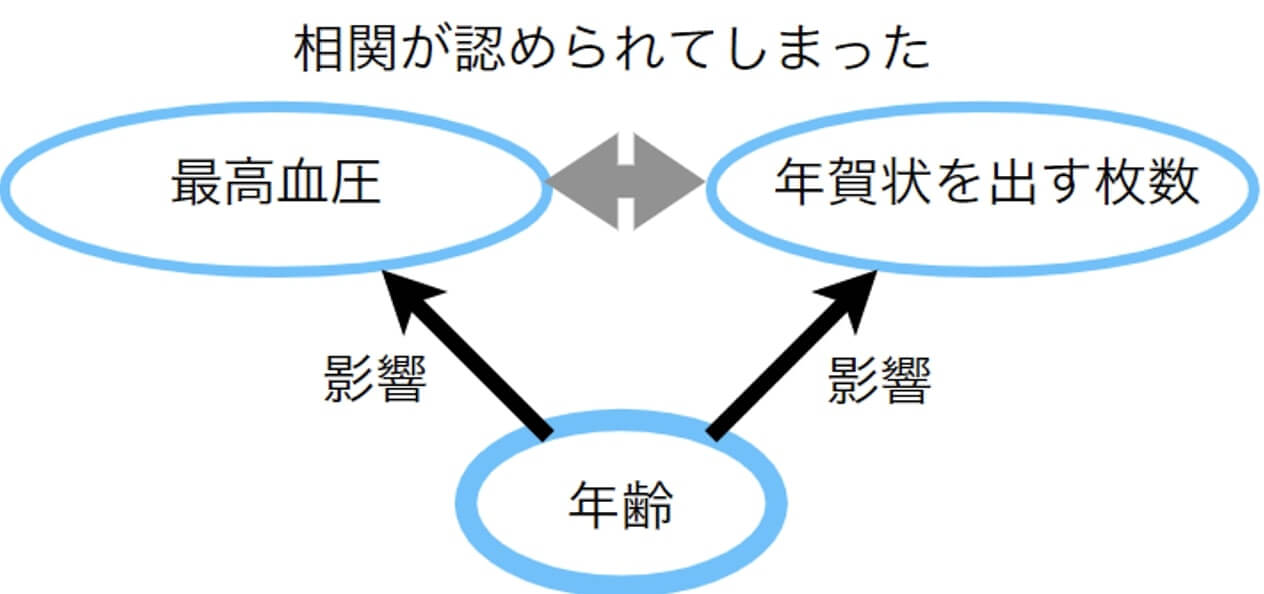
この「年齢」のように、本当に調べたい変数の関連に絡んでくる余計な変数は、交絡変数と呼ばれます。

そして、本当は関連がないものに相関があるように見えてしまう「見せかけの相関」は、疑似相関と呼ばれます。

疑似相関の背景には、共通する第三の変数が存在することが多いです。
（日本における高齢者の割合と東京の夏の平均気温のように「偶然」相関関係があるということもありますが。）

分析は、「差」や「相関」が認められたら終わりではありません。

どういうメカニズムでその差や相関が認められるのか、しっかり考察することが大切です。

U字型分布や逆U字型分布のデータについて|線形ではない関係は相関からは見えてこない

データの分布は、正の相関や負の相関のように直線的な分布をしているとは限りません。

例えば、「一元配置の分散分析」で扱ったデータですが、ストレスがパフォーマンスに及ぼす影響では各条件の課題成績は以下のようになりました。
» 一元配置の分散分析について【参照】

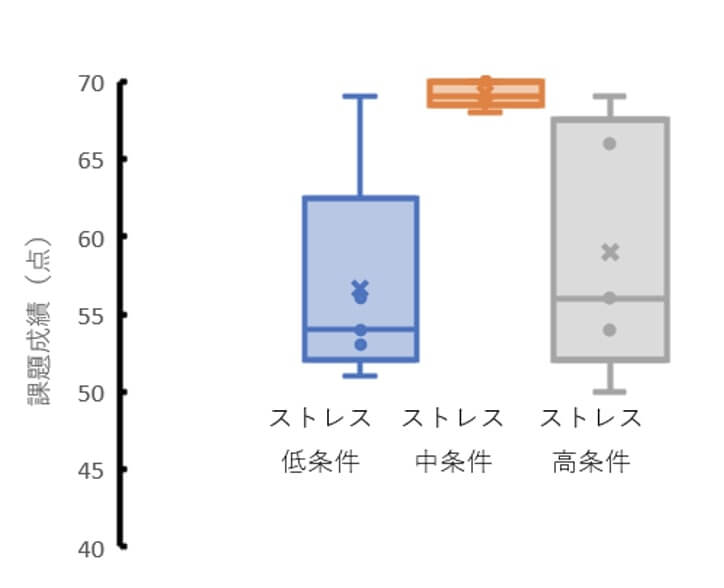元が分散分析のデータのため散布図のようにはできませんが、このグラフから以下のようにデータが分布するだろうと考えられます。

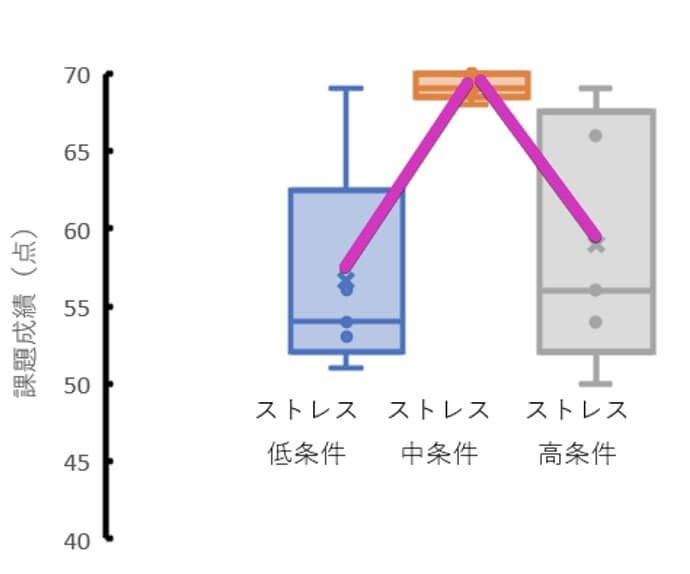
このように、逆U字型（あるいはU字型）のように直線の形で分布していないデータで相関分析しても、相関は認められません。

しかし、ストレスの程度が違うことによって課題成績が違うということはグラフから明白です。

こういった場合もあるので、まずはグラフによる視覚化を行って分布の特徴を確認してから統計を行うことが大切になります。

応用的な相関分析について|相関分析では相関が見えなくても、実は相関があることもある

t検定や分散分析と違って相関分析は色々な変数の関連が複雑に関わってくるため、ただ相関分析をしただけでは相関が見えてこないことがあります。

そういった場合は、ひと工夫することで相関が見えてくることもあります。

そのひと工夫の方法が、偏相関分析と層別解析と呼ばれるものです。

偏相関分析とは|他の変数の影響を取り除くことで見えてくる相関

擬似相関の例として挙げた最高血圧の高さと年賀状を出す枚数との関連のように、相関には本来注目していなかった第三の変数が関わってくることがあります。

この第三の変数の影響を統計的に除いた分析が偏相関分析と呼ばれるものです。
※ 他の変数の影響を統計的に除くことを、統計用語では「統制する」と表現します。

年齢の影響を統制して最高血圧の高さと年賀状を出す枚数について偏相関分析を行ったイメージ図が、以下のものです。

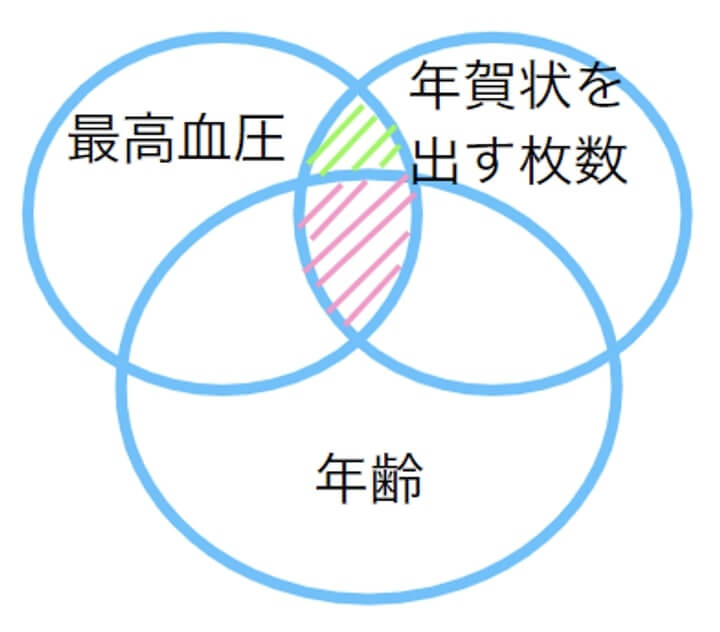最高血圧と年賀状を出す枚数だけを扱った相関分析のときには、それぞれが重なった領域（緑斜線部分とピンク斜線部分を合わせた領域）が相関となりました。

しかし、年齢の影響を統制した偏相関分析を行うことで年齢の影響が取り除かれるため、緑斜線部分だけが最高血圧と年賀状を出す枚数との相関となります。

つまり、最初の最高血圧と年賀状を出す枚数だけを扱った相関分析のときと比べ、最高血圧と年賀状を出す枚数だけが重なる領域（相関）が小さくなるので、相関が小さくなる（場合によっては認められなくなる）といった具合です。

なお、偏相関分析で明らかにされることは疑似相関だけではありません。

相関分析をしていては見つからなかった相関が、偏相関分析を行うことで見つかるということもあります。

実際に偏相関分析によって相関が見つかった研究をご紹介します。

永野氏らが2020年に理学療法科学で発表した研究 では、実習施設への適応感や社会的スキル、無気力感と実習生の学習意欲との関連を調べました。
» 永野ほか、臨床実習における学生の学習意欲に関する研究─実習施設への適応感，社会的スキル，無気力感が与える影響について─　理学療法科学, 35, 879-884.【参照】

相関分析をしていたときには学習意欲のうち競争的な側面と施設への不適応感との相関は認められませんでした。

しかし、学習意欲の自己充実的な側面を始めとして他の全ての変数の影響を統制したら、学習意欲の競争的な側面と施設への不適応感との間には中程度の相関が認められました。

このメカニズムとしては、以下が考えられます。

他の変数との関係から相関が変わるというのは、試行錯誤してデータ分析を行うことや、その分析結果がなぜ出てくるのかを考えることの大切さにつながることだと言えます。

層別解析とは|分析対象を分けることで見えてくる相関

対象者の性質（性別、年代、行動習慣など）によって、分布が異なることがあります。

例えば、労働政策研究・研修機構が21年3月に発表した「就業者のライフキャリア意識調査―仕事、学習、生活に対する意識」を参考にして作成した以下の架空データの分布図があります。

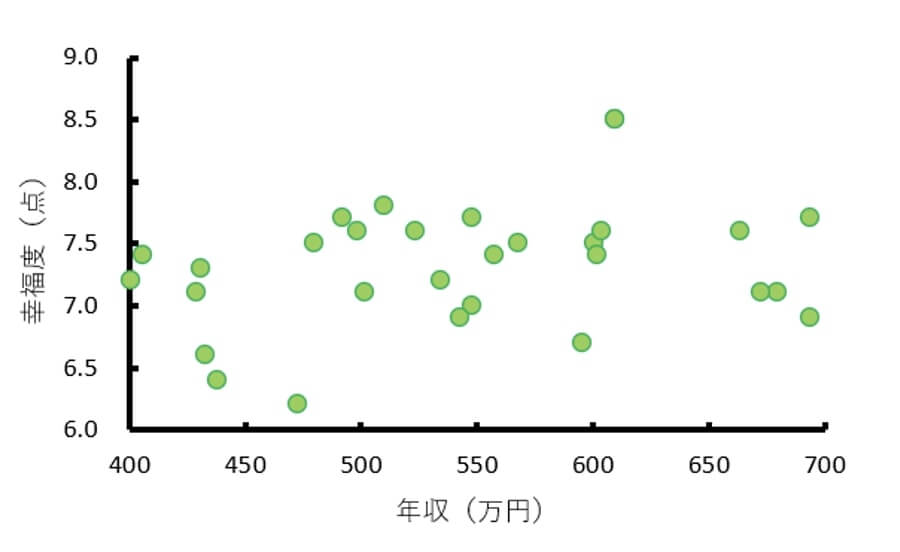多くの方が予想される通り、このデータには相関はありません。

しかし、これを性別で分けて考えてみるとどうなるでしょうか。

青い散布図が男性のデータで、赤い散布図が女性データです。

＜男性＞

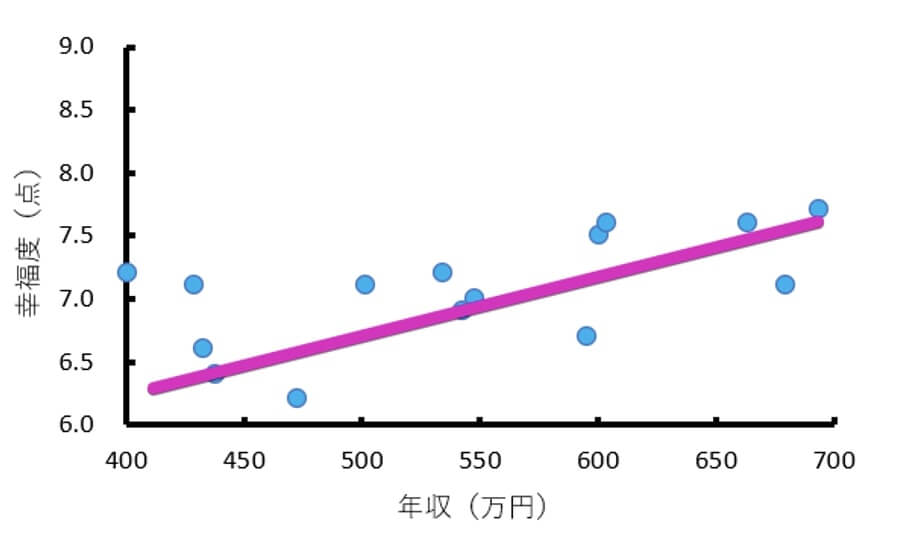＜女性＞

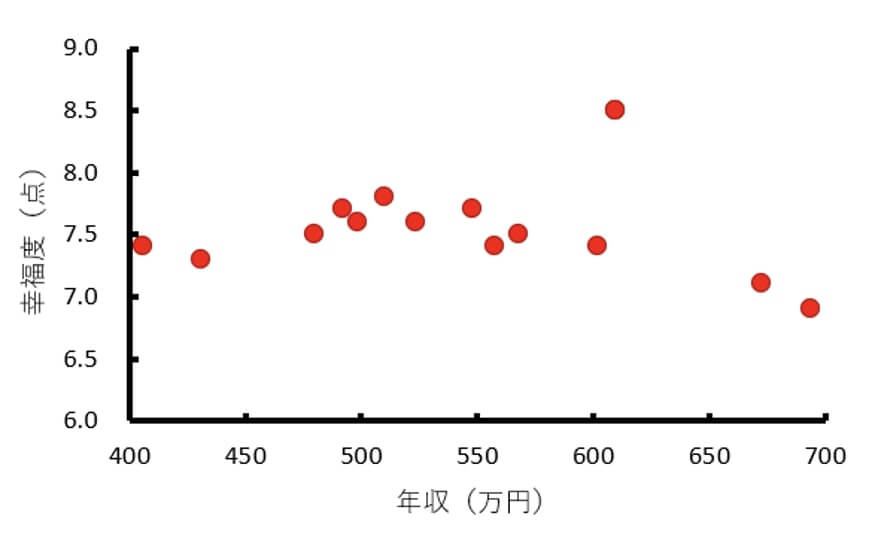
男性の散布図では正の相関が見られるのに対して、女性の散布図ではデータの散らばりはほぼ横一直線で比例・反比例のようなものは見当たらないことが確認出来るかと思います。

このように、対象者の性質（性別、年代、行動習慣など）によってデータを分けて分析することを層別解析と呼びます。

まとめ

この記事では相関分析、偏相関分析、層別解析について解説してきました。

最初にお話したとおり、この講座では相関係数の計算方法については一切触れていません。

これは、記事の対象者を統計学初心者向けに想定しており、特に統計検定2級では相関係数の公式に関する問題が2017年以降は出題されていないためです。（とはいえ随時更新していく予定です。）

統計検定2級の試験では、相関についての考え方や、散布図からの読み取りなどが多く出題される傾向にあります。この講座では相関分析、偏相関分析、層別解析の考え方を理解して頂ければ十分です。

相関係数の公式などについては、練習問題で補足説明をします。

今回はこれで終了とします。