この記事では傾向スコアマッチングについて主に解説させて頂きます。
記事を読むだけだと理解が深まりにくいかもしれませんので、傾向スコアマッチングの理解を深めるために有益な動画（京都大学大学院の授業の一部）を紹介します。
動画を見て、ある程度理解出来たところで、記事にて復習しましょう。
層別解析とは何か？
講座⑩相関分析で説明した通り、対象者の性質（性別、年代、行動習慣など）によってデータの分布が異なることがあります。
例えば、労働政策研究・研修機構が2021年3月に発表した「就業者のライフキャリア意識調査―仕事、学習、生活に対する意識」を参考にして作成した幸福度と年収の架空データでは、サンプル全体の散布図からは関連は見られませんでした。
＜全体図＞
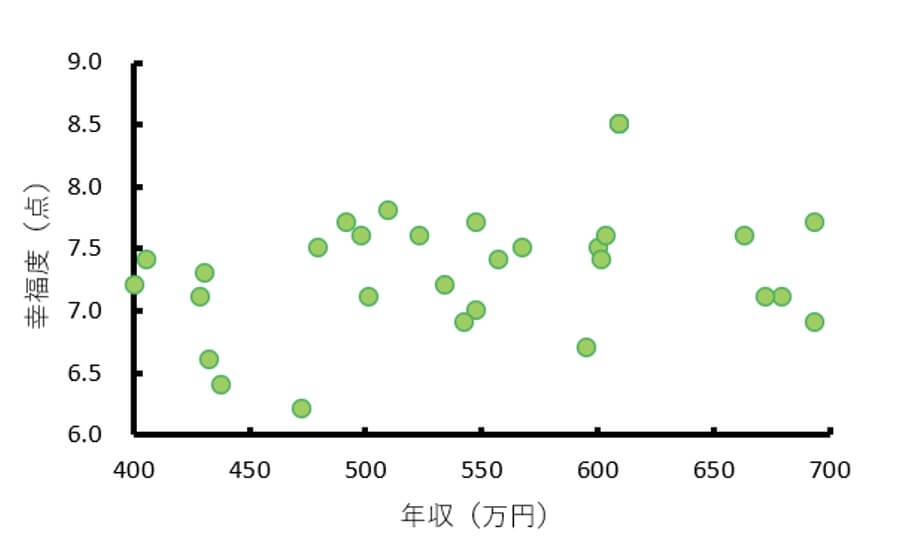
しかし男女別の散布図を作成すると、男性の散布図では正の相関が見られるのに対して、女性の散布図ではデータの散らばりはほぼ横一直線で比例・反比例のようなものは見当たらないことが分かります。
＜男性＞
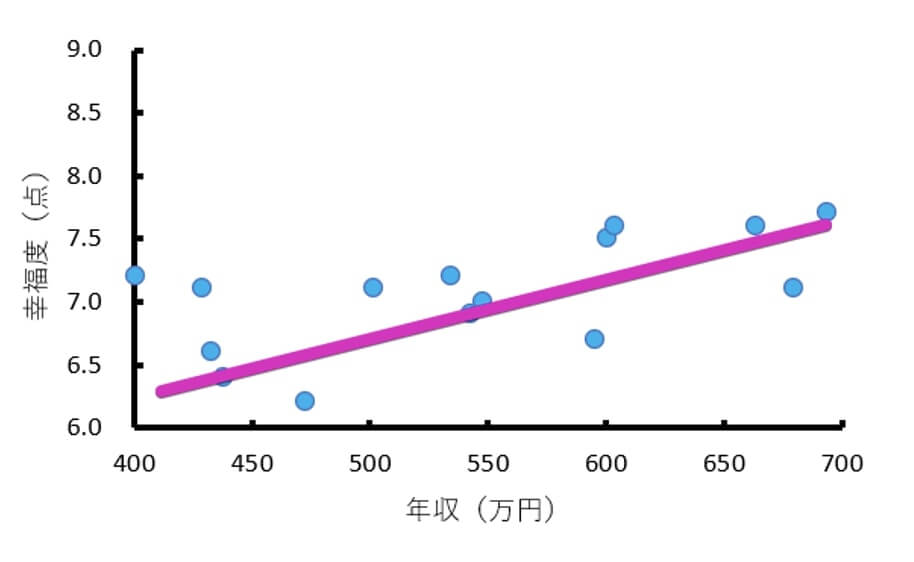
＜女性＞
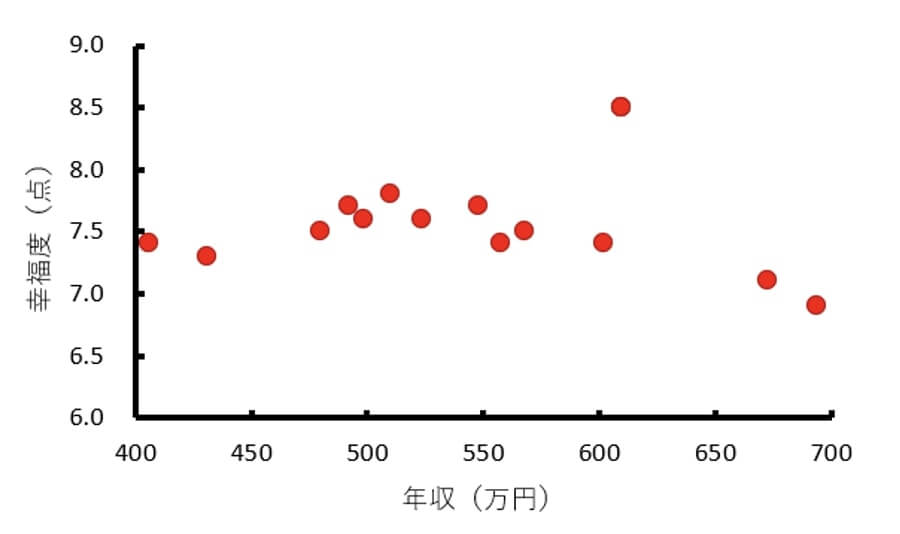
このように全体のデータで分析したときには、変数同士の関連が見られなかったとしても、対象者の性質で分けて分析すると変数同士の関連が認められることがあります。
この分析が層別解析と呼ばれるものです。
層別解析は、ヒストグラムで山が2つある場合にも用いられます。
例えば、以下のヒストグラムは平成18～22年の5年分の国民健康・栄養調査データの男性の1日あたりの食塩摂取量の一部を参考にして作成した架空のデータです。
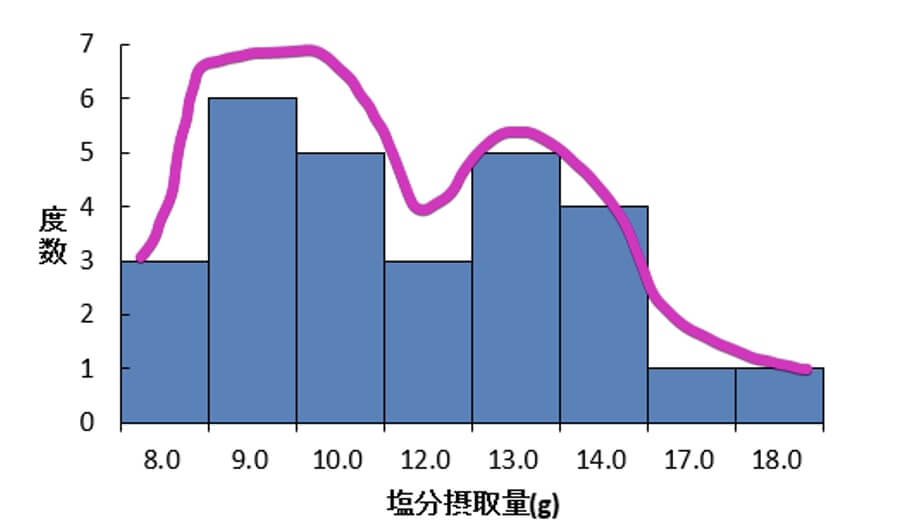
ベル型の正規分布山になっておらず、2つの山があることが見て取れます。
データを集めてきた母集団が異なる場合、このようなヒストグラムが見られることがあります。
例えば、上のヒストグラムは、男性の1日あたりの食塩摂取量が最も多い山梨県と沖縄県の架空データでヒストグラムを作ったもので、山が2つになったのです。
こういった場合は一度に全てをまとめて分析するのは適切ではありません。
山梨県と沖縄県それぞれについて分析する必要があります。
層別解析のメリット｜交絡変数の影響を減らすことができる
層別解析の一番のメリットは、交絡変数の影響を取り除けることです。
実験や調査を行う場合、均質なサンプルからデータを取れれば一番よいのですが、なかなかそうはいきません。
医学分野で特に人間を対象とする研究を行う場合、性別や年齢、食生活や睡眠時間をはじめとする様々な生活習慣の違いなどがデータのばらつきに影響してきます。
その結果、想定した分析結果が出ないことも起こり得ます。
しかし、事前にどんな交絡変数があるかを把握できるのであれば、それに基づいて層別解析を行うことで分析の精度を高めることができます。
層別解析の注意点
層別解析を行うにあたり、
- データ数の問題
- 交絡変数の複雑な関連性
以上のように、①データ数の問題、②交絡変数の複雑な関連性についても注意する必要があります。
層ごとのデータ数は同じぐらいか？そもそもデータ数は十分か？
データを層ごとに分けて分析するということは、サンプルサイズが減ることを意味します。
サンプルサイズが小さくなるということは、（大数の法則から考えると）データがまとまりにくくなるというデメリットもあります。
そのため、検定力（帰無仮説が正しくないときにきちんと帰無仮説を棄却する確率）が低くなり、検定結果が有意になりにくくなります。
また、層ごとにサンプルサイズが同じぐらいであるかも注意しなければなりません。
実際に分析しながら見ていきましょう。
以下は、架空の塩分摂取量と最高血圧データの散布図です。
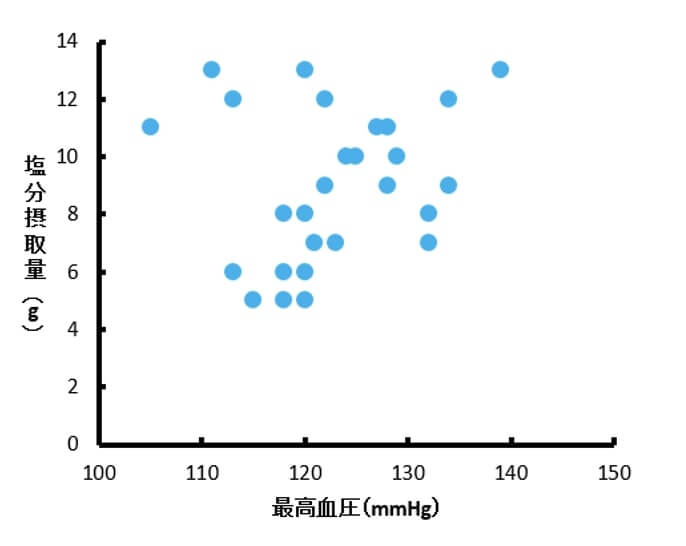この27個のデータについて相関分析を行ったところ、$ r=.18 $となり相関はありませんでした。
しかし、このデータのサンプル数を増やしていくとどうなるでしょうか。
仮に8倍に増やして相関分析をしたところ、$ r=.18 $でも1%水準で有意となりました。
仮に分けた2つの層が同じ分布を示していても、サンプルサイズによっては片方は有意となっても、片方は有意ではないという分析結果が起こり得ることを意味します。
そのため、層別解析を行うにあたり、どちらの層もデータ数は充分であるのか、分布はどのような形なのかを確認する必要があります。
特にサンプルサイズが十分なものでなければ、メインの検証結果というよりも、探索的な追加分析として結果を解釈したほうがよいです。
また、性別のように区分が明確なものもありますが、年齢のように研究者が層の定義を決めなければならないこともあります。
層の定義によって分析結果が変わることもあるため、基準を明確に決めなければなりません。
1つの因子で層別した際の注意点【その因子と相関を持つ他の因子も絡んできていないか？】
変数同士は複雑に絡み合っています。
例えば、一般的に男性のほうが女性よりも最高血圧が高いです。
そこで性別で分けて、層別解析を行うとします。
しかし、これは本当に性別のみで層が分かれているとは言えません。
例えば、一般的に男性のほうが女性よりも飲酒量が多いですが、アルコールも最高血圧を高める効果があります。
そのため、
性別で分けているつもりでも、実は飲酒量で分けているということもあり得ます。
このことも踏まえる必要があるでしょう。
層別解析をRでやってみよう
こちらは現在執筆途中ですが、こちらの記事が分かり易かったので、実践も兼ねて紹介させて頂きます。
» 傾向スコアはRで実践|マッチングとIPWの結果を比較
傾向スコアマッチング｜交絡変数が複数存在する場合
統率したい交絡変数が複数存在する場合には、傾向スコアマッチングを使用します。
ここでは、
- 傾向スコアマッチングとは？
- 傾向スコアマッチングのメリット・デメリット
にFocusを当てて解説していきます。
傾向スコアマッチングとは？
層別解析では、ある1つの交絡変数を元にサンプルを2つの層に分けていました。
しかし、交絡因子となる変数は1つに限定されず、複数となるほうが多いです。
例えば、ある新薬が血圧に及ぼす影響を検討するにあたり、血圧に影響を及ぼしうる交絡変数はたくさん存在します。
性別や年齢、BMI、運動や食事などの生活習慣、仕事のストレス、性格などいくらでもあります。
そんな複数の交絡変数を1つの変数にまとめて統計的分析を行う方法が、傾向スコアマッチングと呼ばれるものです。
傾向スコアでは、サンプルが今割り当てられている治療群/コントロール群に割り当てられる確率を求めます。
理論的には、無作為化割り当てがなされていれば治療群/コントロール群に割り当てられる確率は50%となるはずです。
しかし、特に医学分野の実験では患者さんの背景情報から、本当に無作為に群へ割り当てあれることは多くはありません。
そうすると、治療群とコントロール群でどうしても患者の背景情報が異なる、つまり交絡変数が含まれてくることになります。
そこで、治療の割り当てに影響する変数を使って、治療群/コントロール群に割り当てられる確率を求め、同じ確率同士の患者さん同士で目的変数の差の平均値が有意と言えるほど大きいかを調べるということになるのです。
傾向スコアマッチングのメリット・デメリット
傾向スコアマッチングの一番のメリットは、複数の交絡変数の影響を統計的に取り除けることです。
とはいえ、デメリットもあります。
一番大きなデメリットは、同じ傾向スコアとなる患者さんのマッチングを行うため、サンプル数が少なくなることです。
そのため、検定力が低くなり、有意な結果が得られなくなることもあります。
特に治療群とコントロール群で傾向スコアのヒストグラムの傾向が異なれば、マッチングができるサンプルがさらに少なくなります。
また、当たり前のことではありますが、あらかじめ測定されている変数の影響しか取り除けません。
他にも、性別や体重のように回答しやすいものならよいですが、生活習慣やストレス、性格のように質問項目が多いものは患者さんが回答するうえで負担となります。
そのため、本当に除外しなければならない交絡変数を厳選しておく必要があると言えます。