こんにちは。産婦人科医のとみー(Twitter:@obgyntommy)といいます。
私は普段は画像系の機械学習の研究をさせて頂いてます。
研究の過程で教師なし学習で用いる"GAN"について学習したので、まとめました。
この記事の対象者は機械学習の初学者〜中級者の方です。
そのため、前線で活躍されている方には有益ではありません。
この記事では、まずはGANについて簡単に把握して頂き、次に実際にどの様な例で使用するのかということをGoogle Colaboratoryで手を動かして頂ければ幸いです。
Google Colaboratoryの使い方は以下の記事でまとめています。
-

Google Colaboratoryの使い方【完全マニュアル】
続きを見る
また、実際にGANを使用した教師なし機械学習をGoogle Colaboratoryで行った試行例は以下になります。実際にPythonのコードを動かして頂く事も可能です。
-
Google Colab
続きを見る
誤りがあった場合にはお問い合わせフォームにまでご連絡いただけましたら幸いです。
こちらのスライドに沿って解説させて頂きます。
GAN(敵対的生成ネットワーク)とは
GAN(Genera tive Adversarial Networks. 以下、GAN)は敵対的生成ネットワークと呼ばれ、『生成』とあるように画像などを生成できる技術です。
例えば下図のように、GANのモデルに有名人の画像を学習させると、その後は有名人っぽい画像を出力するようになります。
GANは単純な画像生成の他に、DeepFakeなどの合成技術にも一部使われています。
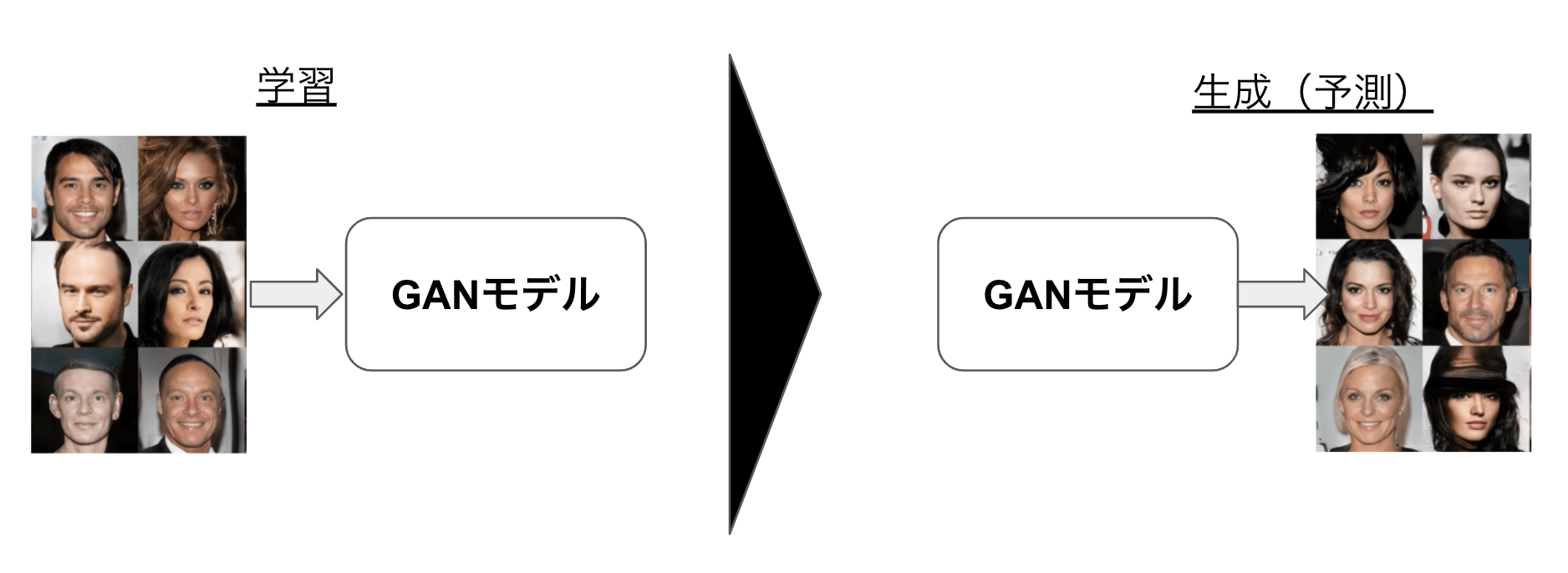
GANのモデル概要
GANの中身は、Generator(以下G)と呼ばれるモデルとDiscriminator(以下D)と呼ばれるモデルの2つで構成されています。
» PythonのGeneratorに関する説明【Python tutorialより引用】
下図のようにGはランダムノイズから本物画像に似た画像(=偽画像)を生成するよう学習され、Dは入力された画像がGによる偽画像か本物画像かを見分けられるように学習されるます。
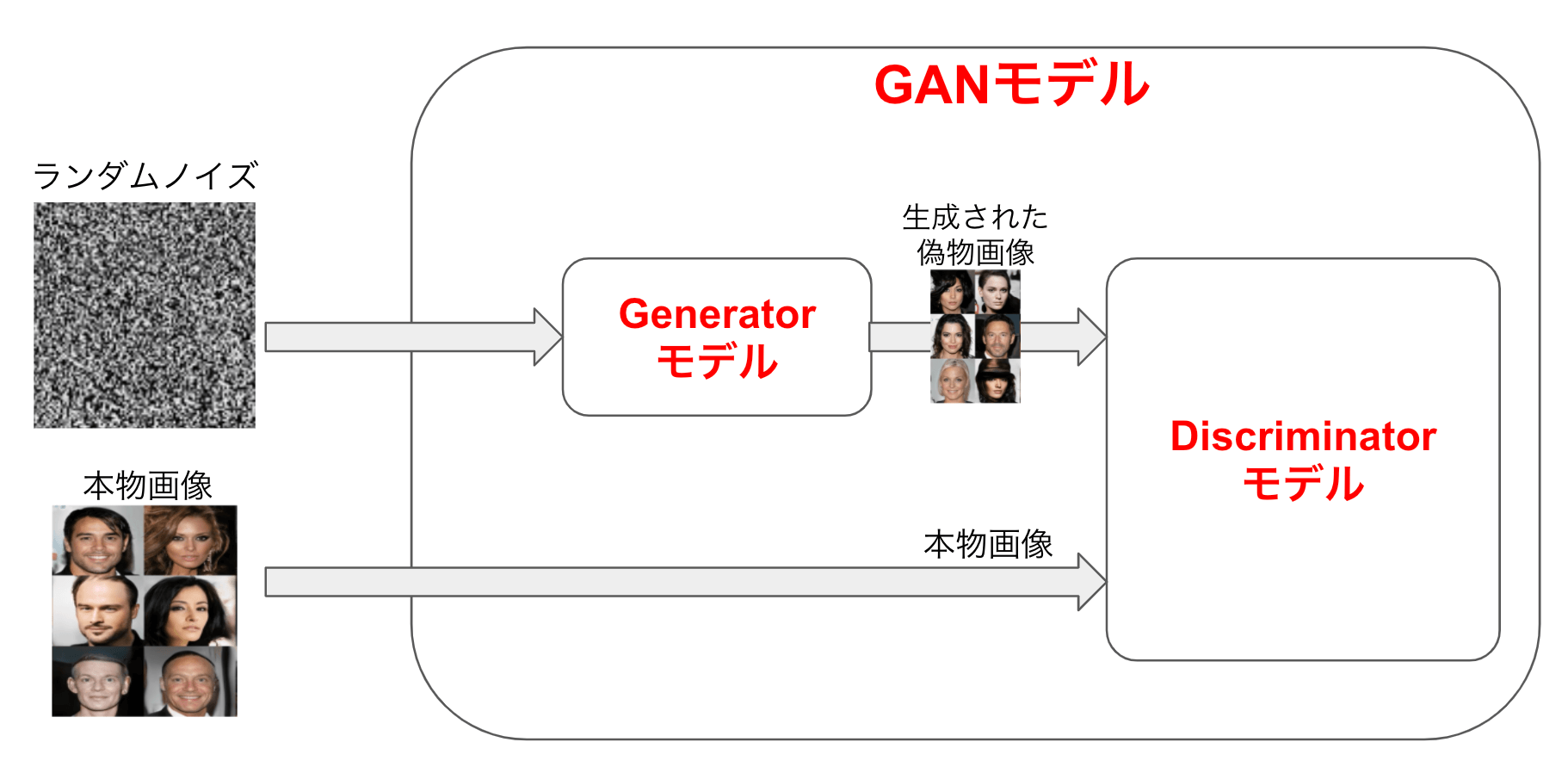
GANを例にすると
前述のGとDに関しては、よくGを『偽通貨を偽造する偽造犯』とDを『偽通貨と本物の通貨を見分ける警察』と表現される事があります。
学習初期は偽造犯Gの偽造する通貨は大したことはないですが、警察Dもそれを中々見分けることが出来ません。
次第に警察Dは学習により見分ける能力が徐々に付いてくると、さらに偽造犯Gは偽通貨を本物っぽくすることで見分けがつかないようにしていきます。
学習後は偽造犯Gは本物と見分けがつかない偽通貨を造るようになり、警察Dは全てを本物の通貨と判断するようになります。
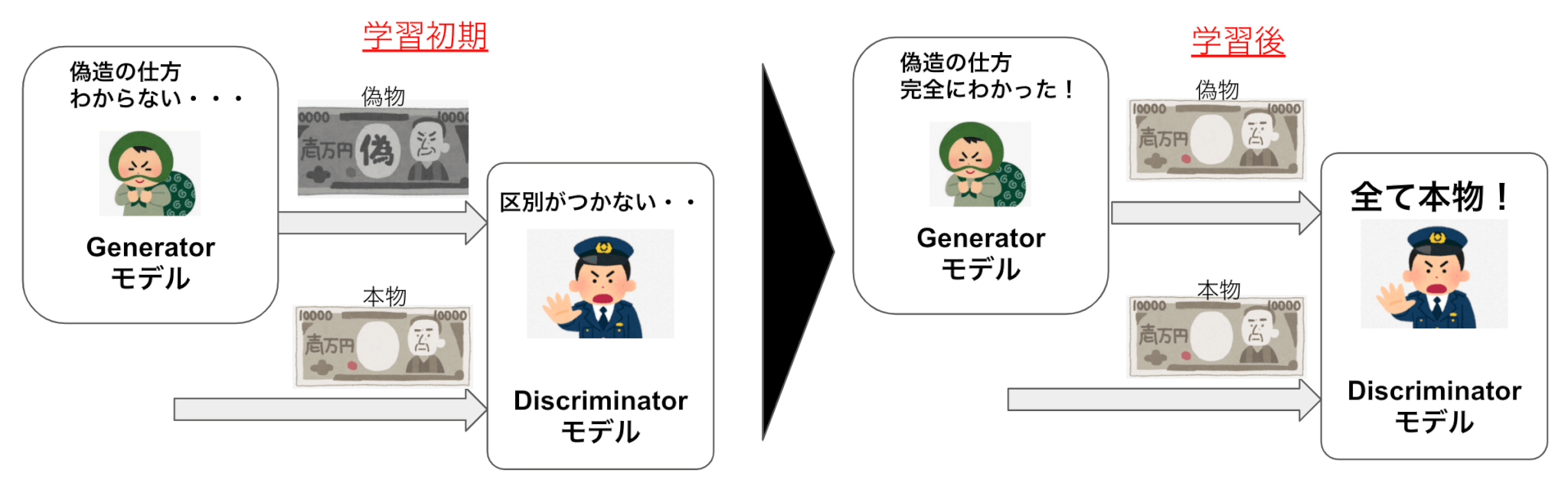
GANの学習の仕組み
Gはノイズから画像を出力できるように、転置畳み込み層などを用いたニューラルネットワークを設定します。
Dは画像から本物/偽物のラベルを出力できるように、畳み込み層を用いたニューラルネットワークを設定します。(こちらは普通のCNNモデルと捉えても問題ないです)
Dの出力と正解ラベル(偽画像か本物画像か)の損失を計算して、その損失をDとGにバックプロパゲーションを行うことによりGとDのネットワークの学習を行います。
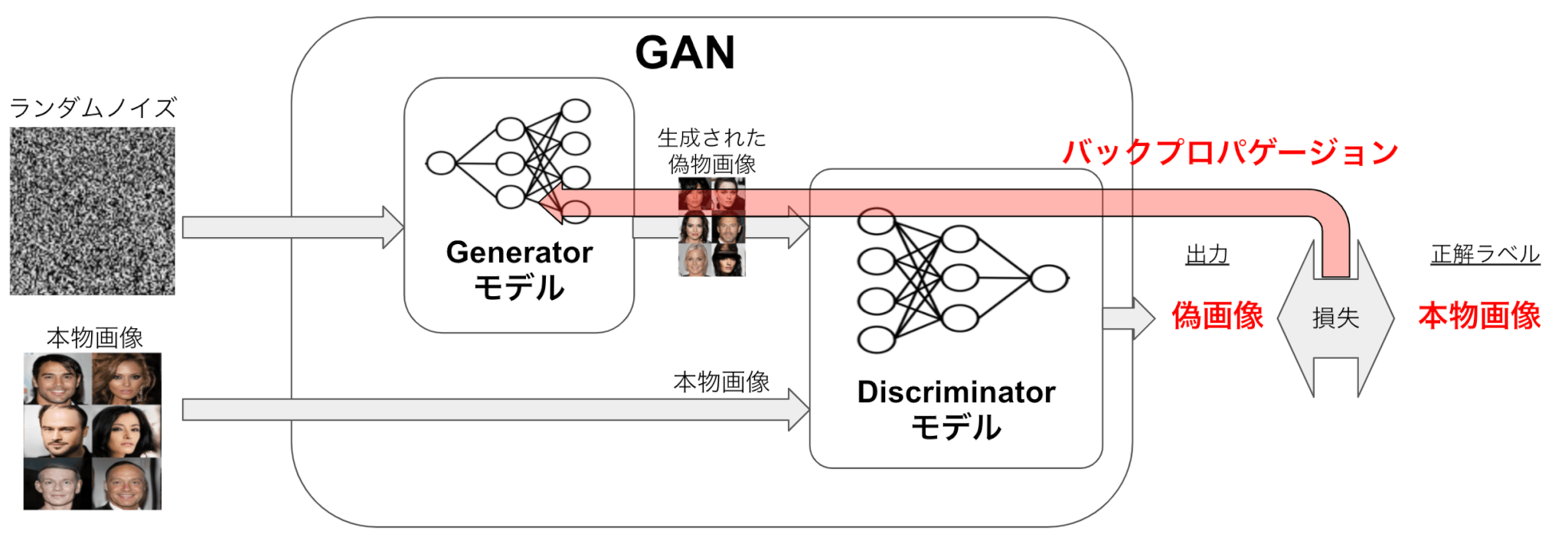
GANを用いた半教師あり学習
GANを用いた手法として半教師ありGANというものがあります。
半教師あり学習とは、教師あり学習において教師ラベルがつけられていないデータも学習に用いる手法でして、教師ラベルをつけるのにコストが大きい際に有効な手法となります。
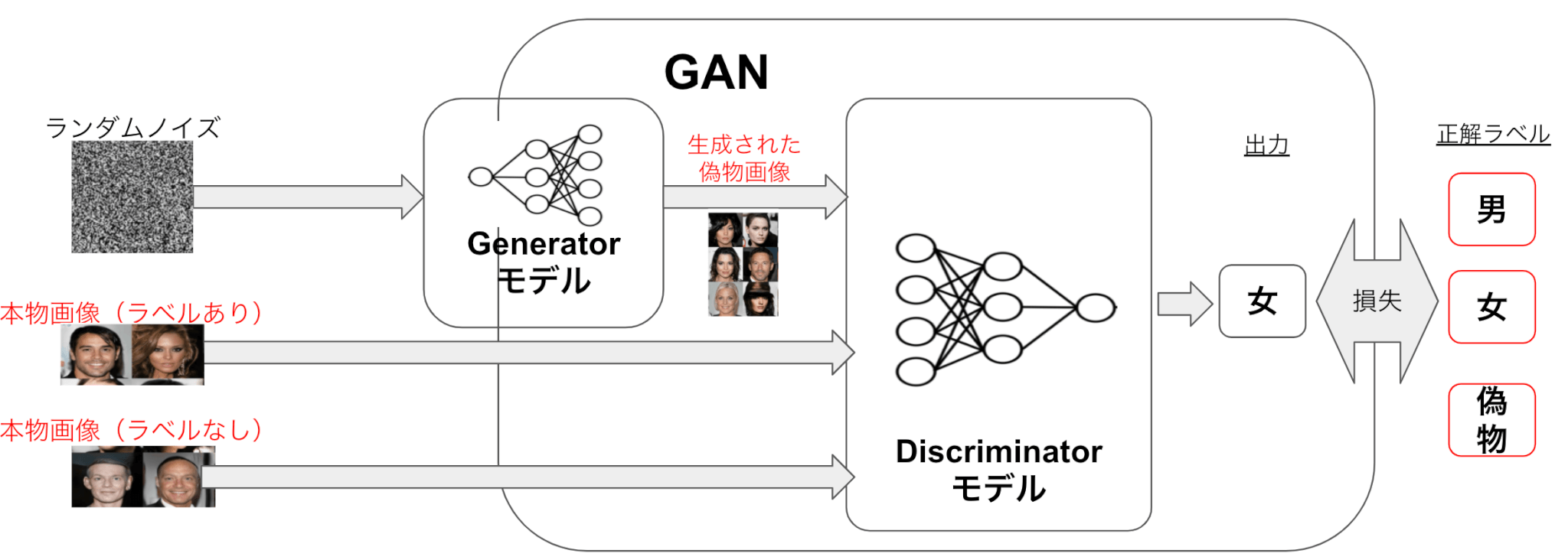
以下の図は半教師ありGANの仕組みを示しています。
Gは前述と同様ですが、Dには本物画像のラベルありなし両方のデータを用いて
- 本物画像に関しては画像分類(男か女か)タスク
- 偽物画像に関しては本物画像と見分けるタスク
を解かせ学習させます。それによりラベルなし画像をDの学習に活かすことができ、Dの画像分類性能を従来より向上させることが可能となります。
全体を把握して頂いた後に、以下の練習問題を手を動かして体験して頂ければ幸いです。
それでは次の項で、GANを用いた半教師あり学習による精度向上を実際に行ってみましょう。
GANを用いた半教師あり学習による精度向上の試行
GANを用いての半教師あり学習により、通常の教師あり学習に比べて精度が向上することを確認してみました。
データセットはMNISTを用い、ラベルがついているデータを1000個としています。
半教師あり学習の場合は、このラベルつきのデータ以外も学習データとして用います。
通常の教師あり学習モデルは、GANのDiscriminatorと同じネットワーク構造をもつとして設定します。
In[]
1 | pip install torch==1.4.0 torchvision==0.5.0 |
Out[]

In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | %matplotlib inline import matplotlib.pyplot as plt import torch from torch import optim from torchvision import datasets, transforms from torch.utils.data import DataLoader, Dataset from torch.autograd import Variable from torch.autograd import Variable import torch.nn as nn import torch.nn.functional as F import torchvision.utils as vutils import numpy as np import pandas as pd import random import os import shutil |
MNISTのデータセットのクラスを作成します。
また今回「マスク」という手法を用いて、教師ラベルとして扱う1000個のデータはマスクをせず(1とする) それ以外の教師ラベルがないとするデータはマスクを行う(0で埋める)という方法にしました。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | #MNISTのデータセットのクラス class MnistDataset(Dataset): def __init__(self, image_size, train): self.train = train self.mnist_dataset = self._create_dataset(image_size, train) self.label_mask = self._create_label_mask() def _create_dataset(self, image_size, train): normalize = transforms.Normalize( mean=[0.5], std=[0.5]) transform = transforms.Compose([ transforms.Resize(image_size), transforms.ToTensor(), normalize]) return datasets.MNIST(root='./mnist', download=True, transform=transform, train = train) def _is_train_dataset(self): return True if self.train ==True else False #マスクによりラベル付きのデータを制御する。以下は1000個のみラベルがついていることにし、他はラベルがついていないデータセットとして扱う def _create_label_mask(self): if self._is_train_dataset(): label_mask = np.zeros(len(self.mnist_dataset)) label_mask[0:1000] = 1 np.random.shuffle(label_mask) label_mask = torch.LongTensor(label_mask) return label_mask return None def __len__(self): return len(self.mnist_dataset) def __getitem__(self, idx): data, label = self.mnist_dataset.__getitem__(idx) if self._is_train_dataset(): return data, label, self.label_mask[idx] return data, label |
次にtrain時とtest時それぞれに使用できるDataLoader を利用する関数を定義します。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #DataLoaderを利用する関数の定義 def get_loader(image_size, batch_size): num_workers = 2 mnist_train = MnistDataset(image_size=image_size, train=True) mnist_test = MnistDataset(image_size=image_size, train=False) mnist_loader_train = DataLoader( dataset=mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers ) mnist_loader_test = DataLoader( dataset=mnist_test, batch_size=batch_size, shuffle=True, num_workers=num_workers ) return mnist_loader_train, mnist_loader_test |
次にGeneratorのネットワークを定義します。Generatorは一般的には転置畳み込みと LeakyRelu と呼ばれる活性化関数が用いられます。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | #Generatorの実装 転置畳み込みとBatchNormとLeakyReLUを組み合わせ最後はTanh class Generator(nn.Module): def __init__(self, nz, ngf, alpha, nc): super(Generator, self).__init__() self.main = nn.Sequential( nn.ConvTranspose2d(nz, ngf * 4, 4, 1, 0, bias=False), nn.BatchNorm2d(ngf * 4), nn.LeakyReLU(alpha,inplace=False), nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False), nn.BatchNorm2d(ngf * 2), nn.LeakyReLU(alpha,inplace=False), nn.ConvTranspose2d(ngf * 2, ngf, 4, 2, 1, bias=False), nn.BatchNorm2d(ngf), nn.LeakyReLU(alpha,inplace=False), nn.ConvTranspose2d(ngf, nc, 4, 2, 1, bias=False), nn.Tanh() ) def forward(self, inputs): out = self.main(inputs) return out |
次に Discriminator のネットワークを定義します。
Discriminator は LeakyRelu と呼ばれる活性化関数を使うのですすが、大体は一般的なCNNと一緒です。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | #Discriminatorの実装 畳み込みとBatchNormとLeakyReLUとDropout class Discriminator(nn.Module): def __init__(self, ndf, alpha, nc, drop_rate, num_classes): super(Discriminator, self).__init__() self.main = nn.Sequential( nn.Dropout2d(drop_rate/2.5), nn.Conv2d(nc, ndf, 4, 2, 1, bias=False), nn.LeakyReLU(alpha,inplace=False), nn.Dropout2d(drop_rate), nn.Conv2d(ndf, ndf, 4, 2, 1, bias=False), nn.BatchNorm2d(ndf), nn.LeakyReLU(alpha,inplace=False), nn.Conv2d(ndf, ndf, 4, 2, 1, bias=False), nn.BatchNorm2d(ndf), nn.LeakyReLU(alpha,inplace=False), nn.Dropout2d(drop_rate), nn.Conv2d(ndf, ndf * 2, 3, 1, 1, bias=False), nn.BatchNorm2d(ndf * 2), nn.LeakyReLU(alpha,inplace=False), nn.Conv2d(ndf * 2, ndf * 2, 3, 1, 1, bias=False), nn.BatchNorm2d(ndf * 2), nn.LeakyReLU(alpha,inplace=False), nn.Conv2d(ndf * 2, ndf * 2, 3, 1, 0, bias=False), nn.LeakyReLU(alpha,inplace=False), ) self.features = nn.AvgPool2d(kernel_size=2) #MNISTだと分類ラベル数10とfakeラベル数の1の計11の出力にする self.class_logits = nn.Linear(ndf * 2,num_classes+1) self.gan_logits = GAN_logit(num_classes) self.softmax = nn.Softmax(dim=0) def forward(self, inputs): out = self.main(inputs) features = self.features(out) features = features.squeeze() class_logits = self.class_logits(features) gan_logits = self.gan_logits(class_logits) out = self.softmax(class_logits) return out, class_logits, gan_logits, features |
続いて、このGAN半教師あり学習のモデルが通常の、教師あり学習のみの場合と精度が高いということを確認します。
そのために、一般的な教師あり学習分類モデルを設定します。このモデルのネットワークはDiscriminatorと一緒にしておきます。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | #Classifierの定義 class Classifier(nn.Module): def __init__(self, ndf, alpha, nc, drop_rate, num_classes): super(Classifier, self).__init__() self.main = nn.Sequential( nn.Dropout2d(drop_rate/2.5), nn.Conv2d(nc, ndf, 4, 2, 1, bias=False), nn.LeakyReLU(alpha,inplace=False), nn.Dropout2d(drop_rate), nn.Conv2d(ndf, ndf, 4, 2, 1, bias=False), nn.BatchNorm2d(ndf), nn.LeakyReLU(alpha,inplace=False), nn.Conv2d(ndf, ndf, 4, 2, 1, bias=False), nn.BatchNorm2d(ndf), nn.LeakyReLU(alpha,inplace=False), nn.Dropout2d(drop_rate), nn.Conv2d(ndf, ndf * 2, 3, 1, 1, bias=False), nn.BatchNorm2d(ndf * 2), nn.LeakyReLU(alpha,inplace=False), nn.Conv2d(ndf * 2, ndf * 2, 3, 1, 1, bias=False), nn.BatchNorm2d(ndf * 2), nn.LeakyReLU(alpha,inplace=False), nn.Conv2d(ndf * 2, ndf * 2, 3, 1, 0, bias=False), nn.LeakyReLU(alpha,inplace=False), ) self.features = nn.AvgPool2d(kernel_size=2) #MNISTだと分類ラベル数10とfakeラベル数の1の計11の出力にする self.class_logits = nn.Linear(ndf * 2,num_classes+1) self.gan_logits = GAN_logit(num_classes) self.softmax = nn.Softmax(dim=0) def forward(self, inputs): out = self.main(inputs) features = self.features(out) features = features.squeeze() class_logits = self.class_logits(features) gan_logits = self.gan_logits(class_logits) out = self.softmax(class_logits) return out, class_logits, gan_logits, features |
gan_logit という関数がありますが、こちらはモデルの出力の1つであり非常に簡単にいうと「モデルが入力を本物と判断するほど出力値が高く、偽物と判断するほど出力値が小さくなる」です。
これにより本物偽物判断についての損失計算が可能になります。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #real_inputs値が高いほど、出力が高くなるロジット関数。ここを参考https://www.kaggle.com/grapestone5321/semi-supervised-gan class GAN_logit(nn.Module): def __init__(self, num_classes): super(GAN_logit, self).__init__() self.num_classes = num_classes def forward(self,input): #MNISTだと11次元を分類ラベル10とfakeラベルの1に分ける real_input, fake_input = torch.split(input,self.num_classes,dim=1) fake_input = torch.squeeze(fake_input) #real_inputが大きすぎる際にも数値を安定させるための処理 max_real,_ = torch.max(real_input, 1, keepdim=True) stable_class_logits = real_input - max_real max_real = torch.squeeze(max_real) out = torch.log(torch.sum(torch.exp(stable_class_logits),1)) + max_real - fake_input return out |
続いて重み初期化とonehot処理をする関数を定義します。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #重み初期化関数 def weights_init(module): classname = module.__class__.__name__ if classname.find('Conv') != -1: module.weight.data.normal_(0.0, 0.02) elif classname.find('BatchNorm') != -1: module.weight.data.normal_(1.0, 0.02) module.bias.data.fill_(0) def one_hot(x): label_numpy = x.data.cpu().numpy() label_onehot = np.zeros((label_numpy.shape[0], num_classes + 1)) label_onehot[np.arange(label_numpy.shape[0]), label_numpy] = 1 label_onehot = Variable(torch.FloatTensor(label_onehot)) return label_onehot |
続いてテスト時に使用する関数を定義しておきます。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | # テスト用のメソッド def test_model(model,loader_test,label): correct = 0 num_samples = 0 model.eval() for i, test_data in enumerate(loader_test): test_inputs, test_labels = test_data test_inputs = Variable(test_inputs) test_labels = Variable(test_labels).long().squeeze() out, _, _, _ = model(test_inputs) _, pred_idx = torch.max(out.data, 1) eq = torch.eq(test_labels.data, pred_idx) correct += torch.sum(eq.float()) num_samples += len(test_labels) test_accuracy = correct/max(1.0, 1.0 * num_samples) print('{} Test:\tepoch {}/{}\taccuracy {}'.format(label,epoch, epochs, test_accuracy)) return test_accuracy |
続いて、モデルに関するものを中心にその他の変数を定義します。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | image_size = 32 #MNIST画像サイズ num_classes = 10 batch_size = 64 #バッチサイズ epochs = 80 #エポック数 nz = 100 #Generator入力の乱数の次元 nc = 1 #画素の次元 白黒なので1 alpha = 0.2 #Leaky Reluのα drop_rate = 0.5 #ドロップアウト率 ngf = 64 #G隠れ層のニューロンの基準値 ndf = 64 #D隠れ層のニューロンの基準値 learning_rate = 0.0002 #学習率 beta1 = .5 #Adamのハイパーパラメータ out_dir = './output' last_save_epoch = 1 G_last_save_filename = '{}/G_epoch_{}.pth'.format(out_dir,last_save_epoch) D_last_save_filename = '{}/D_epoch_{}.pth'.format(out_dir,last_save_epoch) cls_last_save_filename = '{}/cls_epoch_{}.pth'.format(out_dir,last_save_epoch) history_filename = '{}/df_history_acc.csv'.format(out_dir) |
Loaderデータの読み込みを行います。
In[]
1 2 | #Loaderデータの読み込み loader_train, loader_test = get_loader(image_size, batch_size) |
Out[]
(略)
モデルやオプティマイザなどのインスタンスを作成します。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 | os.makedirs(out_dir) #Generatorインスタンスの作成 G = Generator(nz,ngf,alpha,nc) #Generator重み初期化 G.apply(weights_init) print(G) #Discriminatorインスタンスの作成 D = Discriminator(ndf,alpha,nc,drop_rate,num_classes) #Discriminator重み初期化 D.apply(weights_init) print(D) #Classifierインスタンスの作成 cls = Classifier(ndf,alpha,nc,drop_rate,num_classes) cls.apply(weights_init) print(cls) #パラメータのロード try: G.load_state_dict(torch.load(G_last_save_filename)) D.load_state_dict(torch.load(D_last_save_filename)) cls.load_state_dict(torch.load(cls_last_save_filename)) print("loaded network params") except: last_save_epoch = 0 print("no network params founded") #パラメータのロード try: df_history =pd.read_csv(history_filename,index_col=0) print("loaded history file") except: print("make new history file") df_history = pd.DataFrame(columns=["d_gan_loss","g_loss","cls_class_loss","test_acc_D","test_acc_cls"]) #損失関数の定義 d_gan_criterion = nn.BCEWithLogitsLoss() d_gan_class_criterion = nn.BCEWithLogitsLoss() #オプティマイザの定義 g_params = list(G.parameters()) d_params = list(D.parameters()) cls_params = list(cls.parameters()) g_optimizer = optim.Adam(g_params, learning_rate, betas=(beta1, 0.999)) d_optimizer = optim.Adam(d_params, learning_rate, betas=(beta1, 0.999)) cls_optimizer = optim.Adam(cls_params, learning_rate, betas=(beta1, 0.999)) noise = torch.FloatTensor(batch_size, nz, 1, 1) fixed_noise = torch.FloatTensor(batch_size, nz, 1, 1).normal_(0, 1) fixed_noise = Variable(fixed_noise) d_gan_labels_real = torch.LongTensor(batch_size) d_gan_labels_fake = torch.LongTensor(batch_size) best_accuracy = 0.0 |
Out[]
(略)
In[]
1 2 3 | #パラメータ保管フォルダの作成 if not os.path.exists(out_dir): os.makedirs(out_dir) |
続いて学習を行います。1epochごとにテストデータを用いて精度の確認を行っています。また、結構時間がかかりましたので注意してください。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 | for epoch in range(1, epochs + 1): if last_save_epoch < epoch: masked_correct = 0 num_samples = 0 D.train() G.train() cls.train() for i, data in enumerate(loader_train): if i >10000000: pass else: g_optimizer.zero_grad() d_optimizer.zero_grad() cls_optimizer.zero_grad() inputs, labels, label_mask = data inputs = Variable(inputs) labels = Variable(labels).long().squeeze() label_mask = Variable(label_mask).float().squeeze() # DiscriminatorのリアルMNISTデータ損失関数計算 d_out, d_class_logits_on_data, d_gan_logits_real, d_sample_features = D(inputs) d_gan_labels_real.resize_as_(labels.data).fill_(1) d_gan_labels_real_var = Variable(d_gan_labels_real).float() d_gan_loss_real = d_gan_criterion(d_gan_logits_real,d_gan_labels_real_var) # DiscriminatorのリアルMNISTデータ損失計算 noise.resize_(labels.data.shape[0], nz, 1, 1).normal_(0, 1) noise_var = Variable(noise) fake = G(noise_var) #Generatorは学習しない # Discriminatorのフェイクデータ損失計算 _, _, d_gan_logits_fake, _ = D(fake.detach()) d_gan_labels_fake.resize_(labels.data.shape[0]).fill_(0) d_gan_labels_fake_var = Variable(d_gan_labels_fake).float() d_gan_loss_fake = d_gan_criterion(d_gan_logits_fake,d_gan_labels_fake_var) # Discriminatorの総損失計算 d_gan_loss = d_gan_loss_real + d_gan_loss_fake # DiscriminatorのリアルMNISTデータ損失関数計算 labels_one_hot = one_hot(labels) d_class_loss_entropy = -torch.sum(labels_one_hot * torch.log(d_out), dim=1) d_class_loss_entropy = d_class_loss_entropy.squeeze() # マスクされたデータは損失に含めないようにする(マスクされてないデータのみラベルありデータの損失として含む) sum_masked = torch.max(torch.Tensor([torch.sum(label_mask.data),1.0])) d_class_loss = torch.sum(label_mask * d_class_loss_entropy) / sum_masked d_loss = d_gan_loss + d_class_loss #グラフを保存 d_loss.backward(retain_graph=True) d_optimizer.step() ##分類器の学習 cls_out, cls_class_logits_on_data, _, _ = cls(inputs) # 分類器の学習のリアルMNISTデータ損失関数計算 cls_class_loss_entropy = -torch.sum(labels_one_hot * torch.log(cls_out), dim=1) cls_class_loss_entropy = cls_class_loss_entropy.squeeze() # マスクされたデータは損失に含めないようにする(マスクされてないデータのみラベルありデータの損失として含む) cls_class_loss = torch.sum(label_mask * cls_class_loss_entropy) / sum_masked cls_class_loss.backward() cls_optimizer.step() #グラフを保存 d_loss.backward(retain_graph=True) d_optimizer.step() g_optimizer.zero_grad() d_optimizer.zero_grad() _, _, _, d_data_features = D(fake) # "feature matching" loss invented by Tim Salimans at OpenAI.以下参考 #https://towardsdatascience.com/semi-supervised-learning-with-gans-9f3cb128c5e data_features_mean = torch.mean(d_data_features, dim=0).squeeze() sample_features_mean = torch.mean(d_sample_features, dim=0).squeeze() g_loss = torch.mean(torch.abs(data_features_mean - sample_features_mean)) g_loss.backward() g_optimizer.step() _, pred_class = torch.max(d_class_logits_on_data, 1) eq = torch.eq(labels, pred_class) correct = torch.sum(eq.float()) masked_correct += torch.sum(label_mask * eq.float()) num_samples += torch.sum(label_mask) if i % 100 == 0: print('Training:\tepoch {}/{}\tD loss {}\tG loss {} \tcls loss {} \tsamples {}/{}'.format(epoch, epochs, d_gan_loss.data.item(), g_loss.data.item(),cls_class_loss.data.item(), i + 1, len(loader_train))) D.eval() cls.eval() test_acc_D = test_model(D,loader_test,"Descriminator") test_acc_cls = test_model(cls,loader_test,"Classifier") #諸々保存 G_filename = '{}/G_epoch_{}.pth'.format(out_dir, epoch) D_filename = '{}/D_epoch_{}.pth'.format(out_dir, epoch) cls_filename = '{}/cls_epoch_{}.pth'.format(out_dir, epoch) torch.save(G.state_dict(), G_filename) torch.save(D.state_dict(), D_filename) torch.save(cls.state_dict(), cls_filename) df_history.loc[epoch,"d_gan_loss"]=d_gan_loss.data.item() df_history.loc[epoch,"g_loss"]= g_loss.data.item() df_history.loc[epoch,"cls_class_loss"]= cls_class_loss.data.item() df_history.loc[epoch,"test_acc_D"]= test_acc_D.data.item() df_history.loc[epoch,"test_acc_cls"]= test_acc_cls.data.item() df_history.to_csv(history_filename,index=False) |
Out[]
(略)
結果と精度結果
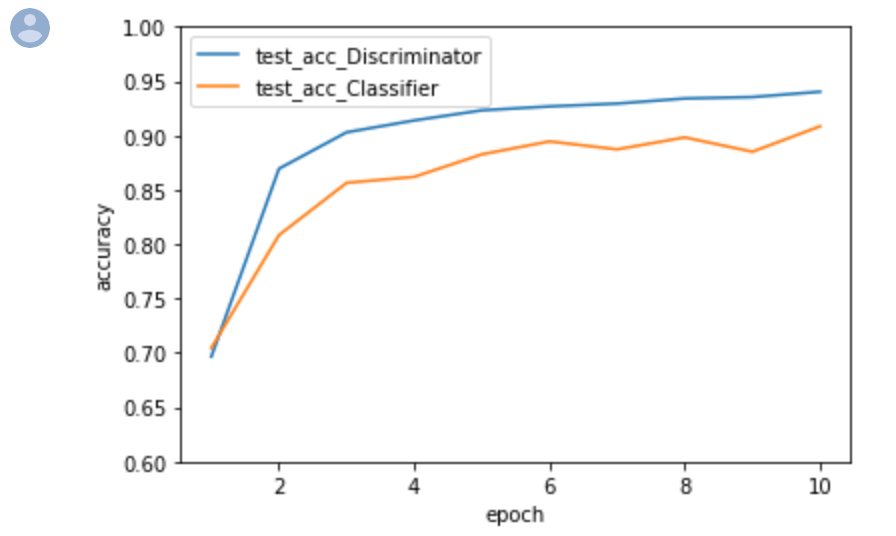
以下は上の結果を用いてテストデータでの分類精度がどのように変化するかを確認しています。
自分が確認した時の結果を入力しているため、皆さんの実行時の結果とは異なっている可能性がありますので異なっていてもご容赦ください。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline x = np.array(list(range(1,11))) arr_D = np.array([0.6965, 0.86940002, 0.90289998, 0.9138, 0.92309999, 0.9267, 0.92930001, 0.93400002, 0.93529999, 0.940199971]) arr_C = np.array([0.70450002, 0.80830002, 0.85640001, 0.86189997, 0.88260001, 0.89450002, 0.8872, 0.89819998, 0.88499999, 0.9083999991]) fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.plot(x, arr_D, label='test_acc_Discriminator') ax.plot(x, arr_C, label='test_acc_Classifier') ax.legend() ax.set_xlabel("epoch") ax.set_ylabel("accuracy") ax.set_ylim(0.6, 1) plt.show() |
Out[]
考察
以上の精度結果について考察です。
GANによる半教師あり学習により、分類モデルの精度を約4%ほど向上させることができました。
結果から、通常のモデルは精度の向上が不安定なことがありますが、半教師あり学習を用いたモデルは比較的安定的に精度が向上する結果となりました。
今後も色々と試してみますが、もしご覧になって頂いた方の中で御気づきの点があった場合には、お問い合わせフォームにまでご連絡いただけましたら幸いです。
Google Colaboratoryを使用してコードを動かす場合には、以下のリンクをご利用ください。
-
Google Colab
続きを見る
今回は以上となります。
