回帰分析について

この記事では以下の相関分析に続いて、同じく関係性の分析の1つである回帰分析を解説します。

「回帰」とは、一般的には「元の場所や状態に戻ること」を意味する言葉ですが、統計学では「因果関係」を意味します。

変数 $y$ に対して変数xがどのように影響を及ぼしているのかを明らかにする、つまりデータの動きを予測する分析が、回帰分析です。

相関分析では1対1の変数同士の関連しか見れませんでしたが、回帰分析では1つの変数 $y$ に対して複数の変数 $x$ がどのように影響を及ぼしているかを調べることができます。

また、回帰分析で扱うのは量的変数ですが、名義尺度であっても「女性$＝0$ 、男性$＝1$ 」のように数値（ダミー変数といいます）に置き換えれば、回帰分析で変数 $x$ とすることができます。

分析できるものが多く、医学分野ではある疾患の原因となる変数を調べたり、マーケティング分野では売上金額につながる変数を明らかにしたりすることができるため、回帰分析は様々な分野で非常に重宝されるのです。

そんな回帰分析について解説していきます。

回帰分析とは何か

帰分析とは、変数 $x$ と変数 $y$ の間に想定した因果関係を明らかにする統計的手法です。

「『想定した因果関係』とは何だろう？」と思われるかもしれません。

これは、$y=a＋bx$ という式で変数 $x$ と変数 $y$ の関係を表そうというものです。

数式にすることで、変数xが増えたり減ったりすることで変数  $y$ がどのように変化するのかを予測できるのです。

例えば、前回の相関分析の講座で扱った1日あたりの塩分摂取量（変数 $x$ ）と最高血圧（変数 $y$ ）についての架空のデータで考えてみましょう。

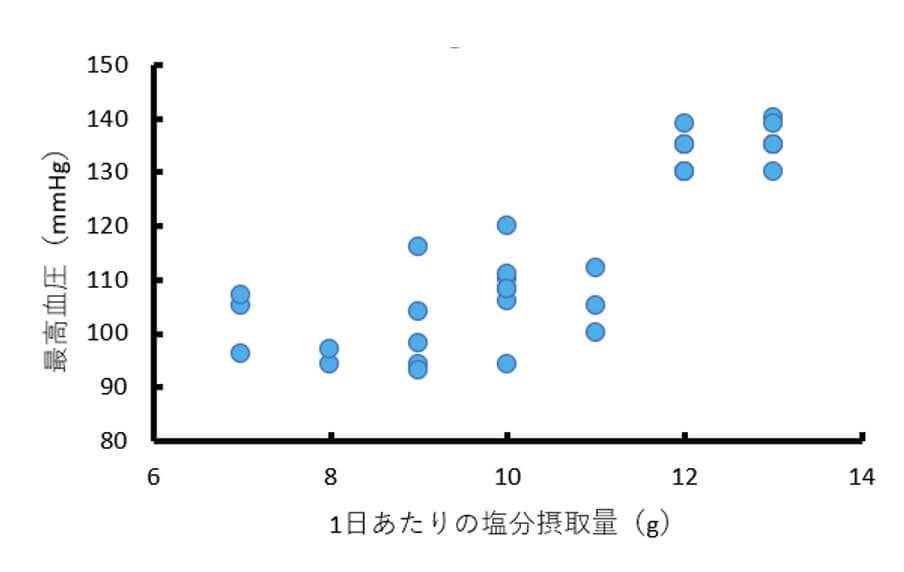
このデータには以下のような直線関係があることが分かりましたよね。

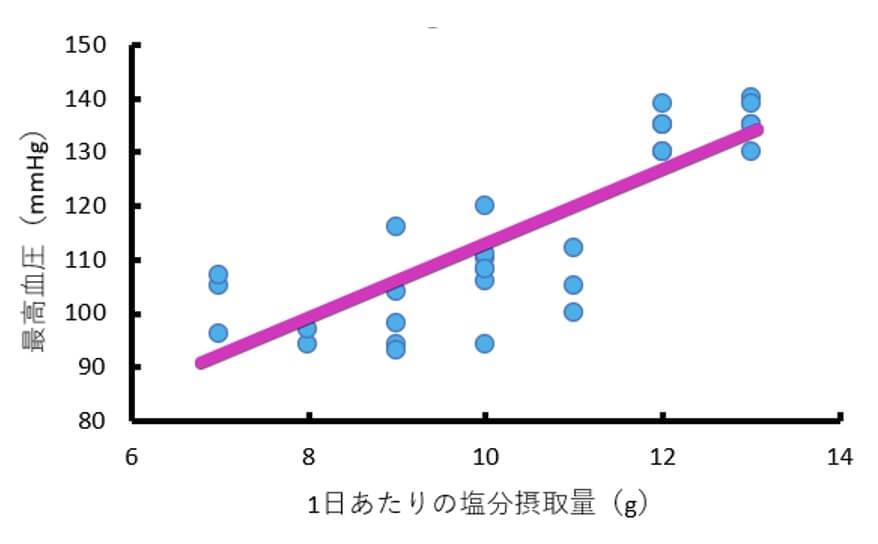これは見て当然ですが、$y=a＋bx$ という式で表される比例関係ですね。

データから $y=a＋bx$ の式を算出するというのが、回帰分析です。

なお、今までは変数 $x$、変数 $y$ と呼んできましたが、予測される側である変数 $y$ は目的変数、予測するのに使われる変数 $x$ は説明変数と呼ばれます。
※「講座①統計的な考え方を身に着けよう」で原因側は説明変数や予測変数、独立変数と呼ばれ、結果側は目的変数や応答変数、従属変数と呼ばれると説明しましたが、回帰分析の場合は説明変数・目的変数と呼ばれることが一般的です。

また、$y=a＋bx$ は回帰方程式（あるいは回帰式）と呼ばれます。

回帰分析と相関分析の違い

相関分析と回帰分析の違いは、分析を行う考え方にあります。

相関分析が変数同士の関連を明らかにするという目的で行われるのに対して、回帰分析では因果関係を明らかにするという目的で行われます。

そのため、仮説検証ための分析を選ぶ際には区別されます。

とはいえ、実際に分析を行うときに相関分析と回帰分析のどちらかだけを行うということはあまりありません。

相関分析で変数同士の関連を確認したうえで、仮説で想定した通り目的変数と関連がある変数を回帰分析の説明変数にするということが多いです。

※ ある変数を回帰分析の説明変数にすることは、「投入する」という言葉で統計学では表現されます。

なお、回帰分析はデータを計算することで $y=a＋bx$ という因果関係の式に当てはめているにすぎません。

説明変数と目的変数を逆にしても、回帰式を組み立てることはできます。

そのため、回帰分析を使えば因果関係を明らかにできるというわけではない点は覚えておかなければなりません。

単回帰分析

単回帰分析とは、目的変数に対して説明変数を1つとする回帰分析のことです。

回帰分析をイメージ化すると、以下の図になります。

ちなみに、相関分析は以下の図になります。

回帰分析では因果関係を明らかにするため右矢印となるのに対して、相関分析では関連を明らかにするため双方向矢印となるのです。

回帰式は、最小二乗法と呼ばれる方法で求められます。

聞き慣れない言葉なので、順を追って説明していきますね。

理論的には回帰分析では $y=a＋bx$ の回帰式を求めていきますが、実際にデータを取るとどうしても測定誤差や偶然によるノイズが混じってしまいます。

そのため、誤差を考慮した $y=a＋bx＋u$（誤差）を計算していくことになるのです。

図で表すと、誤差 $u$ は以下のようになります。

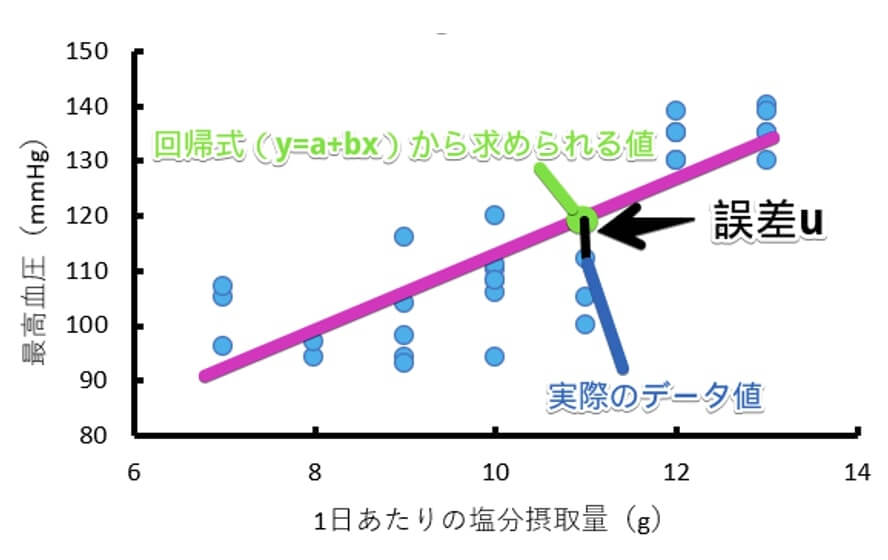
上の図では1つのデータの誤差しか描いていませんが、実際には全てのデータについて誤差があります。

回帰分析では変数 $x$ を使って変数 $y$ を予測するため、できるだけ全てのデータの誤差が少なくなるような回帰式を求めていくのが理想です。

誤差uは実際のデータ値から回帰式の理論値を引くことで算出できますが、そのまますべての誤差を合わせてしまうと0になることもあります。

そのため、誤差 $u$ を二乗したものを全て合わせたものが一番小さくなるような回帰式を求めることになります。

これが「最小二乗法」という名前の由来です。

重回帰分析

「重」が付いている通り、重回帰分析とは説明変数が複数の場合の回帰分析です。

例えば、最高血圧には塩分摂取量だけではなく運動習慣や飲酒習慣、喫煙習慣なども影響を及ぼします。

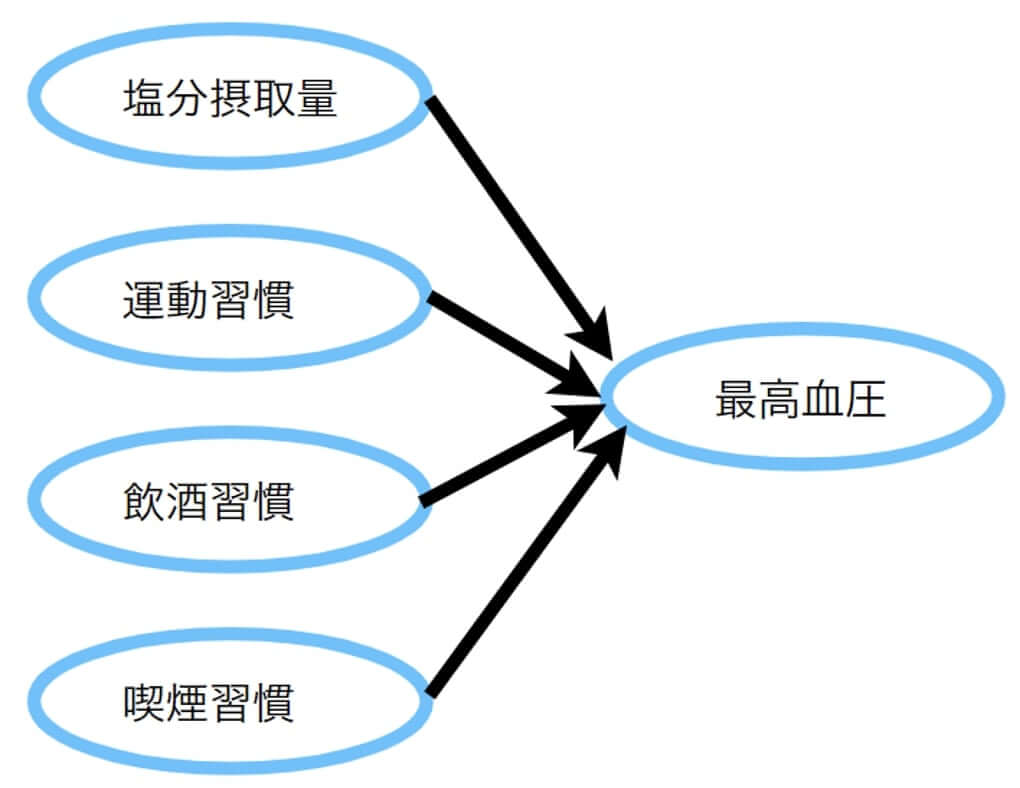
目的変数を最高血圧、説明変数を塩分摂取量や運動習慣、飲酒習慣、喫煙習慣とする重回帰分析を行うと、回帰式は以下のようになります。

$y$（最高血圧）$=a＋b1x1$（塩分摂取量）$+b2x2$（運動習慣）$+b3x3$（飲酒習慣）$+b4x4$（喫煙習慣）

重回帰分析を行うことで目的変数に一番影響を及ぼしているのはどの説明変数かを明らかにすることもできますが、それについては後ほど説明します。

回帰分析にまつわる様々な用語

「8-1.回帰分析とは何か？」では説明変数に目的変数、回帰方程式（あるいは回帰式）と多くの用語が出てきました。

しかし、回帰分析では他にも様々な用語が出てきます。

用語を押さえておかなければ、回帰分析の結果を正しく理解することができません。

ここでは回帰分析にまつわる様々な用語を説明していきます。

特に回帰分析の結果を読み取るうえで大切なのは、①回帰係数（偏回帰係数や標準偏回帰係数含む）と、②決定係数（あるいは説明率、自由度調整済み決定係数を含む）です。

回帰係数（偏回帰係数）、標準偏回帰係数

回帰係数とは、回帰式 $y=a＋bx$ の「$b$」のことです。

つまり、回帰係数とは説明変数が目的変数に及ぼす影響の程度と言うことができます。

なお、重回帰分析の場合は回帰係数ではなく偏回帰係数（B）と呼ばれます。

偏相関分析でも「偏」という言葉が出てきましたが、これは他の変数の影響を統計的に取り除いたときの当該変数の影響力・重みを意味する統計用語です。

例えば、先の目的変数を最高血圧、説明変数を塩分摂取量や運動習慣、飲酒習慣、喫煙習慣とする重回帰分析の場合なら、塩分摂取量や運動習慣、飲酒習慣の値を変化させず、喫煙習慣の値だけが変わったときに最高血圧がどのように変化するのかが分かります。

とはいえ、塩分摂取量は  g/日、運動習慣は  時間/週 だから単位が異なります。

そのため、偏回帰係数は比較できません。

そこで、説明変数や目的変数を標準化してから偏回帰係数を算出することになりますが、こうして求められるものが標準偏回帰係数（β）と呼ばれるものです。

単位の違いという問題がクリアされるので、標準偏回帰係数同士を比べることでどの変数が特に重要か判断することができます。

決定係数（説明率）、重相関、自由度調整済み決定係数

決定係数（ $\mathrm{R}^{2}$ ）とは、回帰分析で得られた回帰式がどのくらい実際のデータを予測できているかを意味します。

例えば、以下の2つの回帰直線は同じものですが、左の回帰直線のほうが実際のデータに近いですよね。

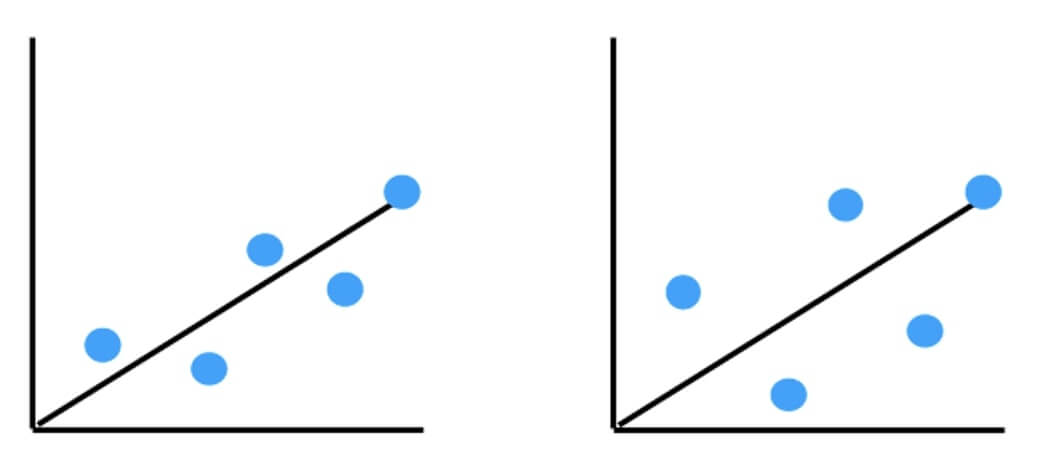
このような場合に決定係数が高いということになります。

目的変数の動きを説明変数でよく「説明」できていると言い換えることもできるため、決定係数は説明率と呼ばれることもあります。

相関係数には大きさの目安がありましたが、決定係数も $0～1$ までの値を取り、$1$ に近いほど目的変数の動きを説明変数でよく説明できていると解釈されます。

経験的に決定係数が $0.5$ 以上あれば回帰式の精度が高いと考える統計学者もいますが、相関係数と違ってそこまで絶対的な基準ではありません。

例えば、深刻な病気の要因を明らかにするという研究の場合、決定係数が0.5ほど高くはなくても病気の要因である以上軽んじることはできないからです。

また、人の考えのようにノイズが多いものを使う場合はデータの誤差が多いため、決定係数がそこまで高くなりにくいです。

重回帰分析では単回帰分析と比べて説明変数が増えますが、データのバラツキを説明するものが増えるので、説明変数を増やすほど必然的に決定係数は1に近くなります。

とはいえ、これは説明変数が増えたから決定係数が少し増えただけなのか、その説明変数は目的変数を十分に説明できるものだから決定係数が増えたのか判断したいところです。

そこで、重回帰分析では説明変数の数を考慮した自由度調整済み決定係数と呼ばれるものを使って、重回帰式の当てはまりの良さを見ていきます。

なお、決定係数と関連する用語に重相関係数（$R$）というものがあります。

相関係数と名前は似ていますが、重相関係数とは実際の目的変数の値と、分析の結果得られた重回帰式を使って計算した推定値との相関係数のことです。

重相関係数の記号 $R$ から察している人もいるかもしれませんが、重相関係数を2乗したものが決定係数となります。

重相関係数も0から1の値を取り、1に近いほど回帰式の当てはまりが高いことを意味します。

残差

残差と誤差。

名前は似ていますが、その意味は少し違います。

誤差 $u$ は「単回帰分析」で説明した通り、理論上の回帰式 $y=a＋bx$ から求められる理論上の値と実際のデータとの差を意味します。

一方で残差 $e$ とは、実際のデータから計算された回帰式 $\hat{y}=\hat{a}+\hat{b} x$ から求められる値と実際のデータとの差を意味します。

イメージをイラスト化したものが、以下の図です。

回帰式 $y=a＋bx$ はあくまでも理論上のものであり、実際のデータにはどうしても誤差やノイズが混じるため、誤差uはどうやっても計算できません。

しかし、残差 $e$ は得られたデータを元に推定した回帰式を使って求めるので、計算することができます。

回帰分析の基本的な結果の見方は、以下の2点です。

この2点になります。

しかし、それら以外に残差が回帰分析の結果の判断に使われることがあります。

それが残差分析と呼ばれる方法です。

講座⑨「$\chi 2$検定」でも「$\chi 2$検定の結果の残差分析」というものがありましたが、回帰分析における残差分析とは残差のバラツキがないか確認するというものです。

統計手法で確認するほうが正確ではありますが、残差データを並べたプロットでも残差のバラツキをある程度は確認できます。

妥当な回帰式が得られていれば、以下の図のように残差はバラバラになります。

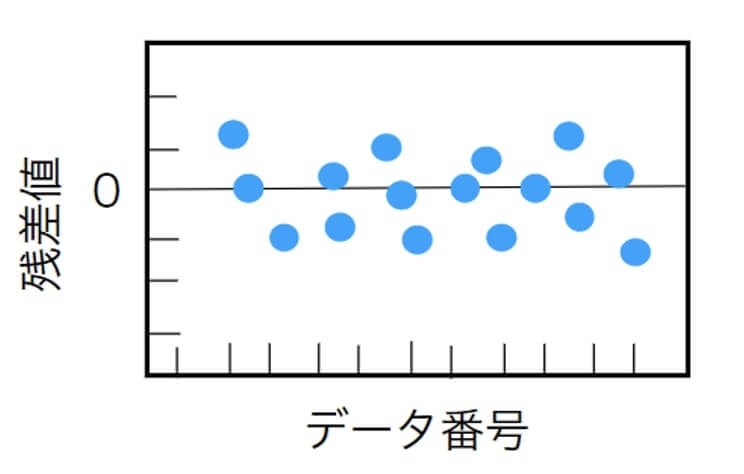
しかし、残差に増加傾向や減少傾向、あるいは外れ値などが見られる場合は、違う変数を説明変数とするなど回帰式を見直したほうがよいです。

なお、残差を確認する統計手法にはBreusch-Paganテスト，Whiteテストなどがありますが、難しい話になるため割愛します。

予測値

予測値とは、回帰分析で求められた $\hat{y}=\hat{a}+\hat{b} x$ を使って任意の $x$ に対する目的変数の値です。

あくまでも統計上の値であり、実際の値との間には残差があることには注意が必要です。

とはいえ、ある程度は売上高がいくらか予測できるので、特にマーケティングで重宝されます。

回帰分析、重回帰分析の結果の見方

実際に回帰分析や重回帰分析の結果を出力したものを見ていきましょう。

講座⑩相関分析の「7-1-2.相関の種類～正の相関、負の相関、無相関～」で用いた架空の1日あたりの塩分摂取量と最高血圧のデータを使って、まずは回帰分析をします。

目的変数を最高血圧、説明変数を塩分摂取量として回帰分析を行ったところ、以下の出力結果が得られました。

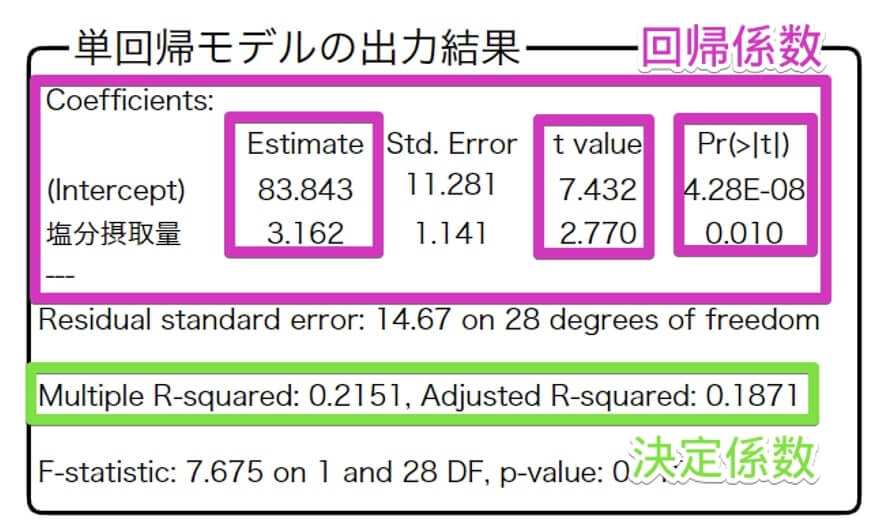
特に注目していただきたいのは、回帰係数の枠と、決定係数の枠です。

回帰係数の枠のうち、注目すべきはEstimateとt value、 $Pr(>|t|)$ です。

決定係数の枠では、左のMultiple R-Squaredが決定係数、右のAdjust R-Squaredが自由度調整済みの決定係数です。

次に目的変数を最高血圧、説明変数を塩分摂取量と運動時間として重回帰分析を行ったところ、以下の出力結果が得られました。

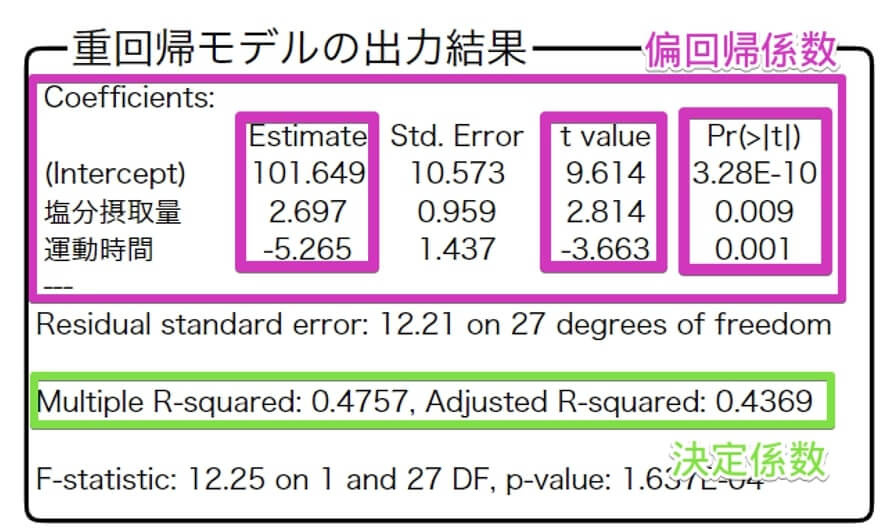
注目してほしいのは、決定係数の枠のAdjust R-Squaredです。

先ほどの目的変数を最高血圧、説明変数を塩分摂取量とした回帰分析では $0.1871$ だったのが $0.4369$ に増えています。

やはり説明変数が多いほど、目的変数のバラツキを説明できると言えます。

また、塩分摂取量と運動時間の $t$ 値の絶対値を比較すると、運動時間のほうが大きいことが分かります。

このことから、この架空データにおいては運動時間のほうが塩分摂取量よりも最高血圧には強い影響を及ぼすと言えそうです。

なお、偏回帰係数なので $t$ 値で比較していますが、標準化偏回帰係数を算出していればそのまま説明変数の影響の強さを比較できます。

重回帰分析の注意点|多重共線性

このように目的変数を説明する変数を調べたり、その変数がどのくらいの強さで目的変数を説明するのかを明らかにしたりできるため、重回帰分析はとても便利な分析です。

とはいえ、重回帰分析では多重共線性（マルチコ）という問題に注意しなければなりません。

統計学において、多重共線性（単に共線性とも略される）とは、重回帰モデルにおいて、説明変数の中に、相関係数が高い組み合わせがあることをいう（例：体重とBMI）。 重回帰分析の際、説明変数を増やすほど決定係数が高くなりやすいために、より多くの説明変数を入れ、多重共線性を起こす可能性がある。

» Weblio辞書より引用

相関分析と同じで、重回帰分析も結局のところデータの関連を分析で見ているにすぎません。

そのため、お互いに相関の強い説明変数を同じ回帰式に入れてしまうと、端的に言えば分析結果がこんがらがってしまいます。

回帰係数の符号が本来とは逆の符号となったり、決定係数が妙に大きな値になったりするなど、正しい分析ができなくなります。

そのため、多重共線性の問題は避けなければなりません。

だから、重回帰分析を行う前に相関分析を行い、説明変数同士の相関を事前に確認する手続きが非常に重要になるのです。

以上が回帰分析や重回帰分析の基本的な考え方や結果の見方です。

相関分析同様、回帰分析や重回帰分析も実際に行おうとなると必要とされるデータ数の多さや計算式の複雑さから、統計ソフトがどうしても必要になります。（個人的にはRがおすすめです）

そのため、統計検定2級への合格レベルを目指すのなら、まずは考え方や結果の見方を抑えておくことが肝要です。