こんにちは。産婦人科医のとみーです。(Twitter:@obgyntommy)
本記事では記述統計のグラフについて、特にデータの特徴やグラフの見方について解説していきます。
対象としては【統計検定2級の取得を目指している方】に向けた記事となります。
記述統計について、実験や調査で集めたデータを視覚的に分かりやすく伝える方法がグラフです。
しかし、集めたデータを表現するのにピッタリなグラフを選択できなければ、せっかくのグラフも何を伝えたいか分からないものになってしまいます。
この記事では、データの特徴にあったグラフにはどんなものがあるかをお話ししていきます。
量的変数を利用すると様々な種類のグラフが作れる

グラフの目的とは、ずばりデータを視覚的に分かりやすくすることです。
どんなグラフであっても数値を使って作ることから、特に量的変数では色々なグラフが作れます。
量的変数とは、値が連続的に変化するもので、連続変量ともいう。
質的変数とは、値と値とのあいだの距離が任意のもので、離散変量ともいう。
基本の円グラフと棒グラフ、折れ線グラフ。どう使い分けるのか。
グラフと言えば、円グラフや棒グラフ、折れ線グラフなどがすぐに思い浮かぶと思います。
それぞれどんなデータのときに使うものか分かりますか。
実際に見ていきましょう。
全部で100%となるデータには円グラフ
構成比など全部で100%となる円グラフを表す場合は円グラフが適しています。
例えば以下は、2019年の日本の年少人口(0~14歳)と生産年齢人口(15~64歳)、老年人口(65歳以上)の構成のグラフです。
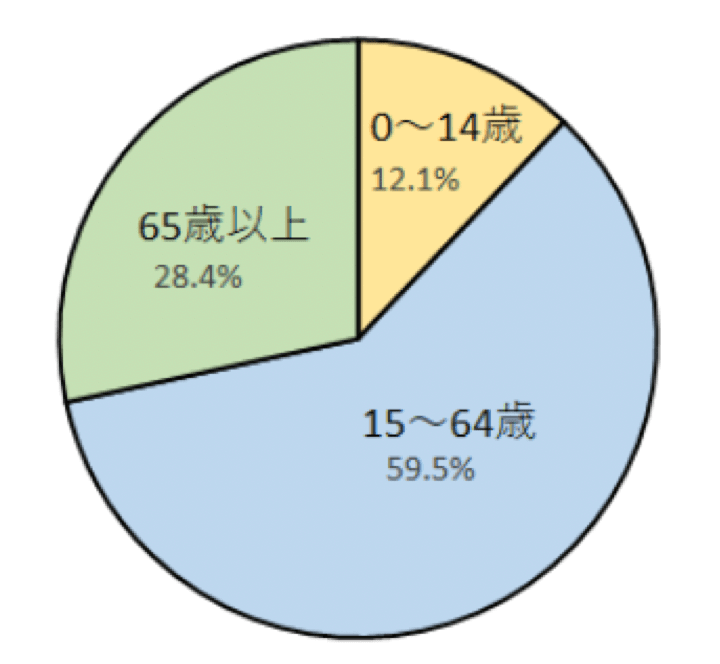
日本の年齢別人工の構成比
» 総務省統計局「人口推計(2019年(令和元年)10月1日現在)結果の要約」【引用】
円は1周すると必ず360°になります。
そのため、円になっていると「全体で100%」ということを一目で理解させることができるのです。
時系列データなら折れ線グラフ
変化を見る時系列データなら折れ線グラフが適しています。
例えば、以下は日本の生産年齢人口の推移のグラフです。
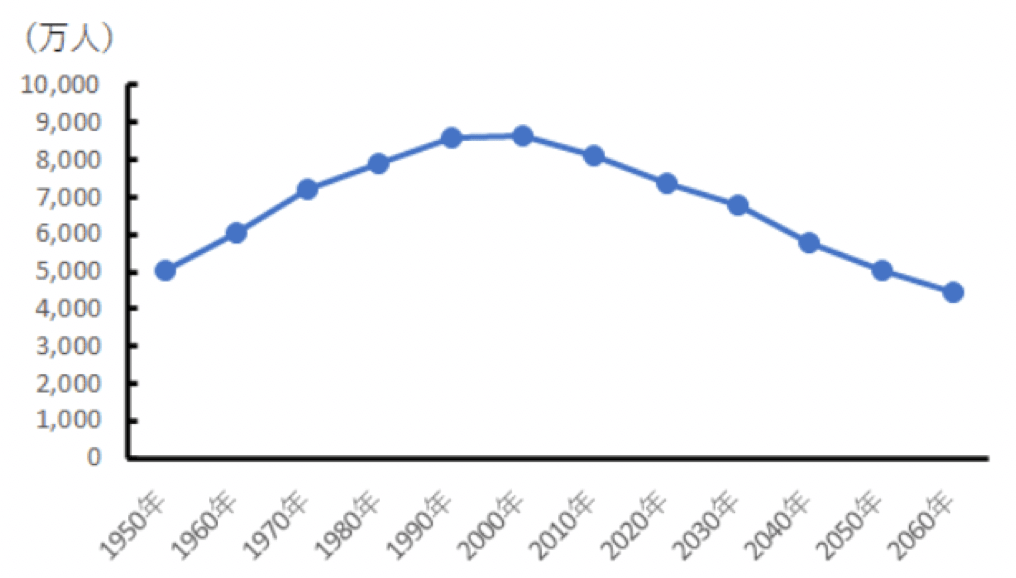
日本の生産年齢人口の推移
折れ線グラフは各データが線で繋がっているので、目線で変化を追うことができます。
そのため、変化を直感的にイメージしやすいのです。
なお、統計検定2級を受験する上では、
- その①:不平等の程度を示した曲線グラフ
- その②:周期性を含んだ折れ線グラフも出題されたことがあるので、知っておく必要があります
以上が非常に重要な点になります。
その①:不平等の程度を示した曲線グラフ
所得格差や人口集中の不平等といった事象の集中を表すのにローレンツ曲線と呼ばれるグラフが使われます。
ローレンツ曲線とは、ある分布を持つ事象について、確率変数が取り得る値を変数とし、確率変数の値が与えられた変数の値を超えない範囲における確率変数と対応する確率の積の和を、その分布に対する確率変数の期待値で割って規格化したものとして与えられる関数の幾何学的な表現のことである。
例えば、日本の各都道府県のデパート数格差を示すローレンツ曲線を見てみましょう。
まず、都道府県数ごとのデパートの数は以下の表の通りです 。
16県ではデパート数は1つしかないのに、1都では27個あることが分かります。
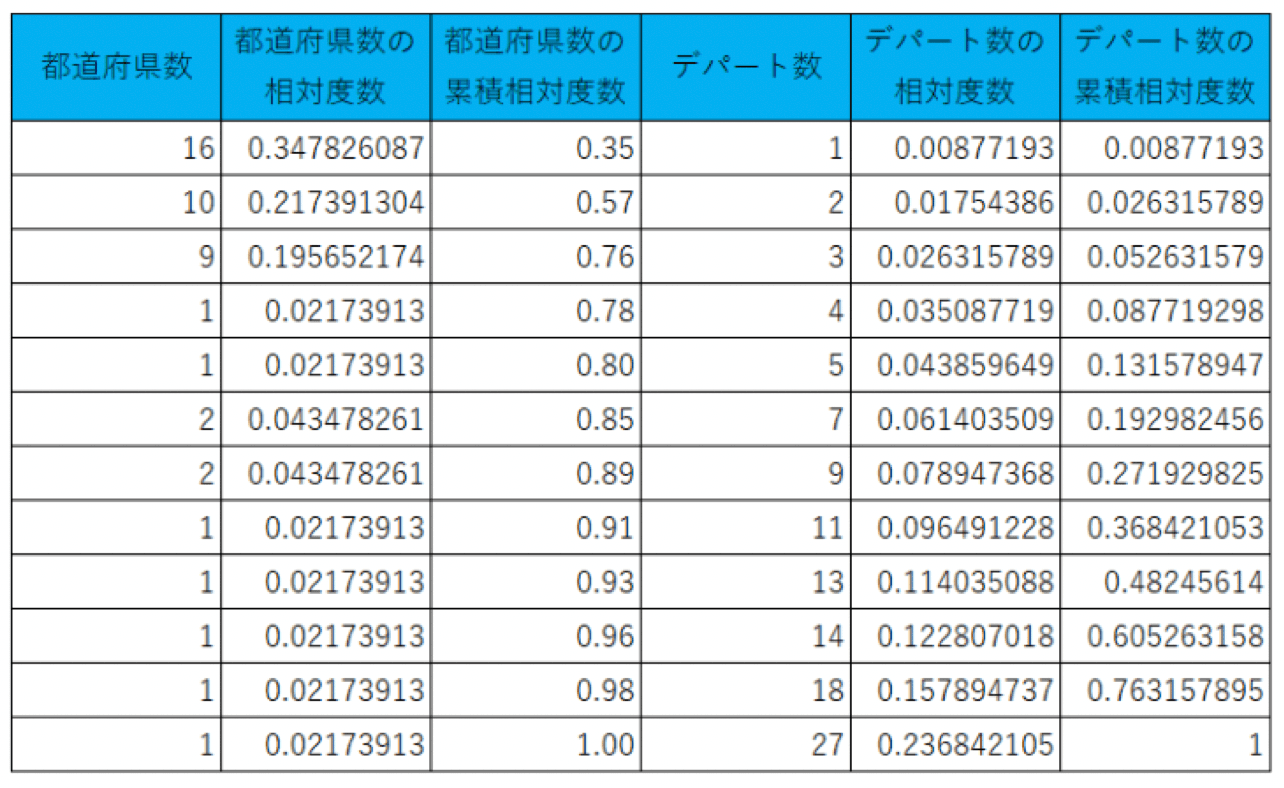
都道府県数ごとのデパートの数
この表の都道府県数の累積相対度数とデパート数の累積相対度数を使って作ったのが、以下のローレンツ曲線です。
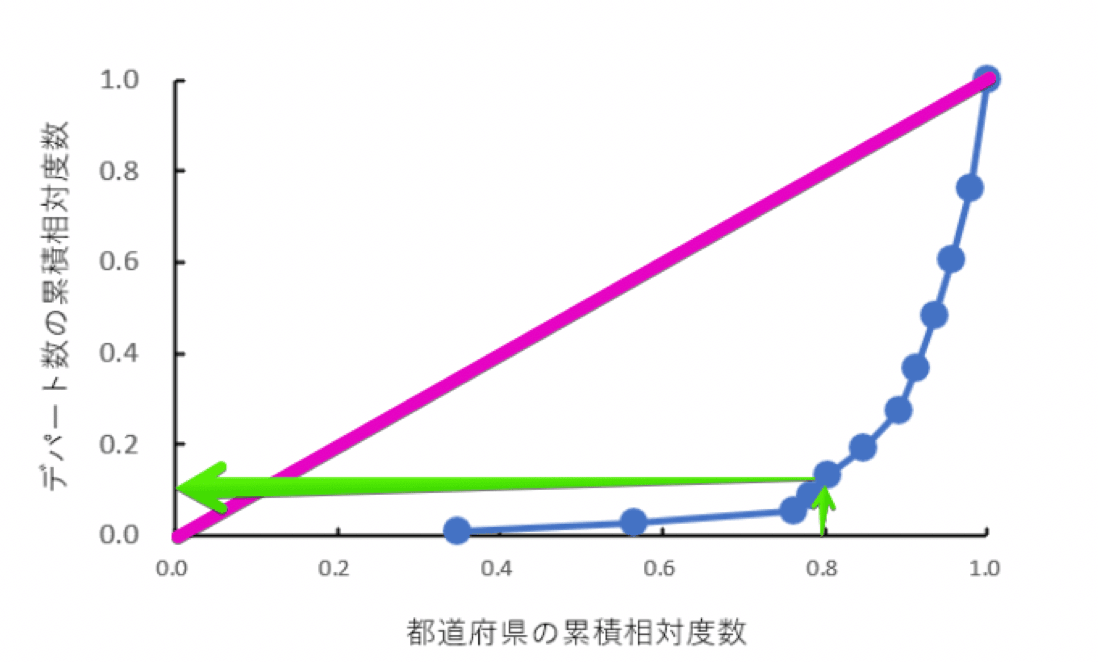
都道府県数ごとのデパート数のローレンツ曲線
黄緑の矢印をたどってみると、約80%の道府県内で全国のすべてのデパート数の10%ほどがあるということが分かります。
逆にいうと、残りの約20%の都府県内に90%ものデパートがあるということです。
このようにデパートの分布は不均等であることが分かります。
ちなみにピンクの線は格差がないときの線((0, 0) と(1, 1) を結んだ線)で、完全平等線と呼ばれます。
ローレンツ曲線のカーブが完全平等線と離れるほど格差が大きいことになります。
ローレンツ曲線の格差を表す数値として、ジニ係数と呼ばれるものがあります。
完全平等線とローレンツ曲線が同じ場合はジニ係数は 0 となり、格差が大きいほど1に近づいていきます。
その②:周期性を含んだ折れ線グラフ
周期的なデータとして心拍変動があげられます。
ただ、例えばお店の売上や気候変動など周期性がありそうなデータだけど本当に周期性があるのかを知りたいことがあると思います。
そういったときにはコレログラムと呼ばれるグラフを使えば、データに周期性があるかが分かります。
例として、ある架空の心拍変動のデータから見てみましょう。
以下のデータ(赤線)は、架空の心電図です。
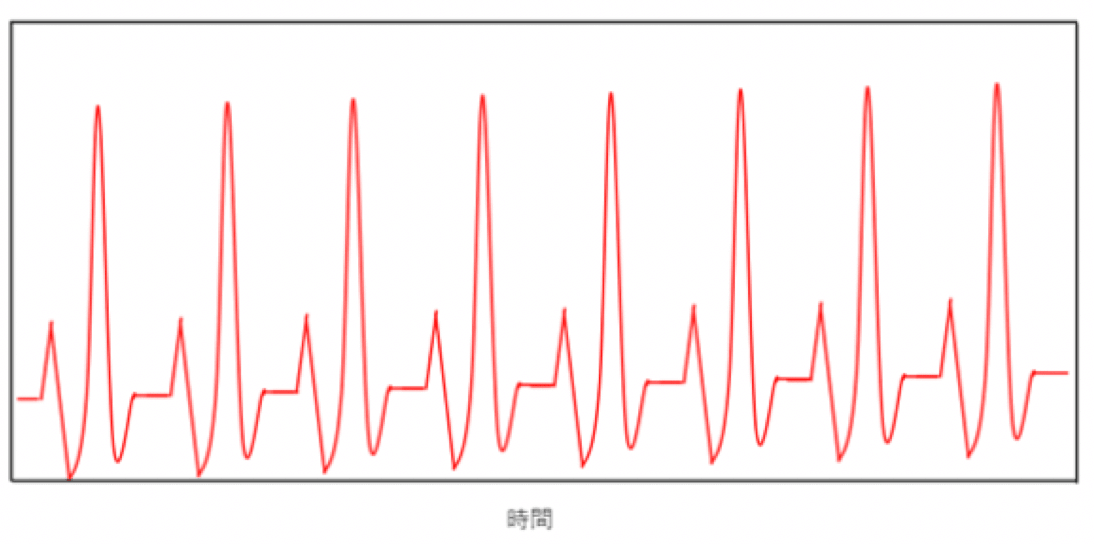
心電図
これを〇秒ずらすと、以下のように元のデータ(赤線)とずらしたデータ(青線)が少し離れます。
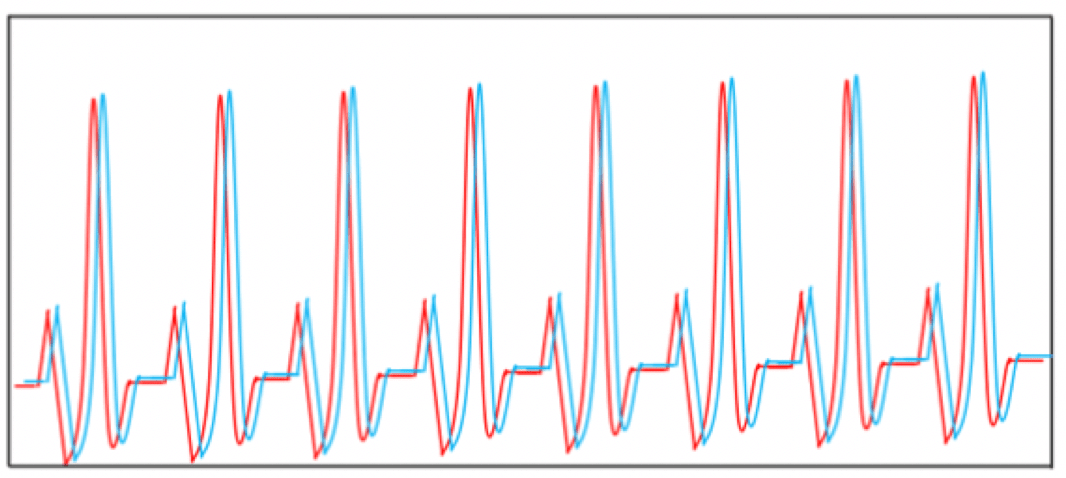
〇秒ずらした時の心電図
さらに△秒ずらすと、以下のように元のデータ(赤線)とずらしたデータ(青線)が大きく離れます。
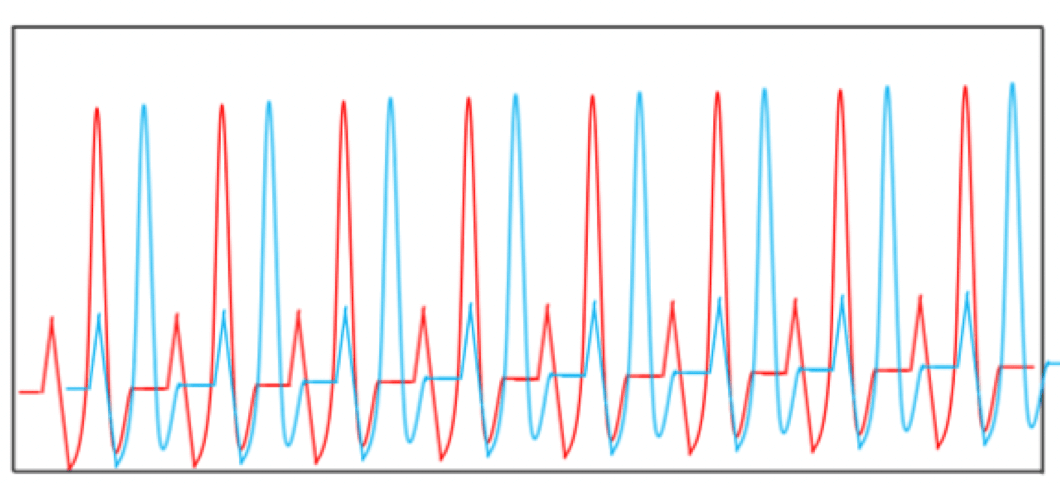
△秒ずらした時の心電図
そして□秒ずらすと、以下のように元のデータ(赤線)とずらしたデータ(青線)が再び重なります。
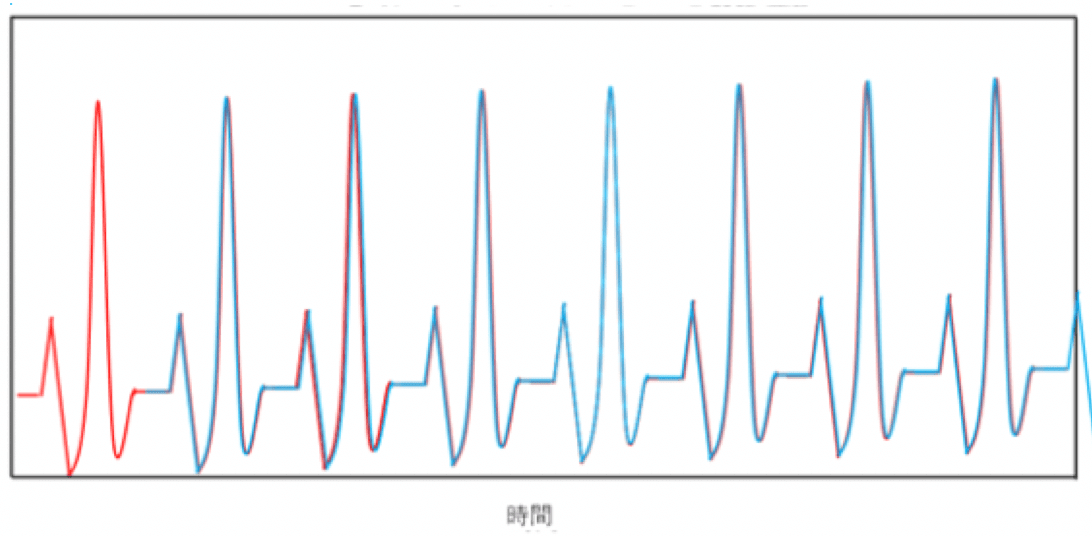
□秒ずらした時の心電図
ずらした時間をラグと呼びますが、ラグと自己相関係数(現在のデータと過去のデータがどれほど似ているかを表した数値)を表したグラフがコレログラムです。
自己相関係数は-1~1の値を取りますが、1ほど似ている、0に近づくほど似ていない、そして-1に近づくほど真逆であることを意味します。
今回の心拍変動のコレログラムのイメージは以下のようになります。
最初は全く同じですが、徐々にずれていき、また同じになっていくという形になります。
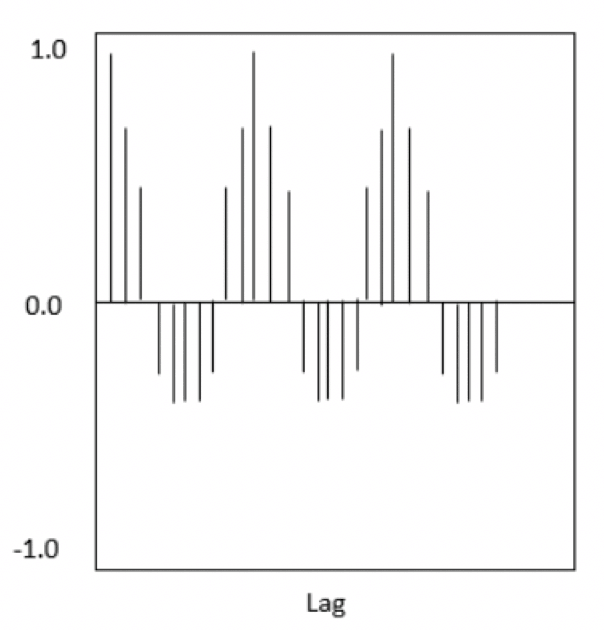
心電図のコレログラムのイメージ
なお、今回はあくまでもずっと一定の心拍変動だったので、コレログラムも常に同じ形を繰り返しています。
例えば徐々にピークのR波が下がっていったのなら、重なったときに元のR波との間にズレが生じるので、コレログラムの山なりも徐々に小さくなるという形に変わってきます。
連続性のないデータは棒グラフ
データの大小を比較したい場合は、棒グラフが適しています。
例えば、以下は北海道・東北地方の2019年の総人口のグラフです。
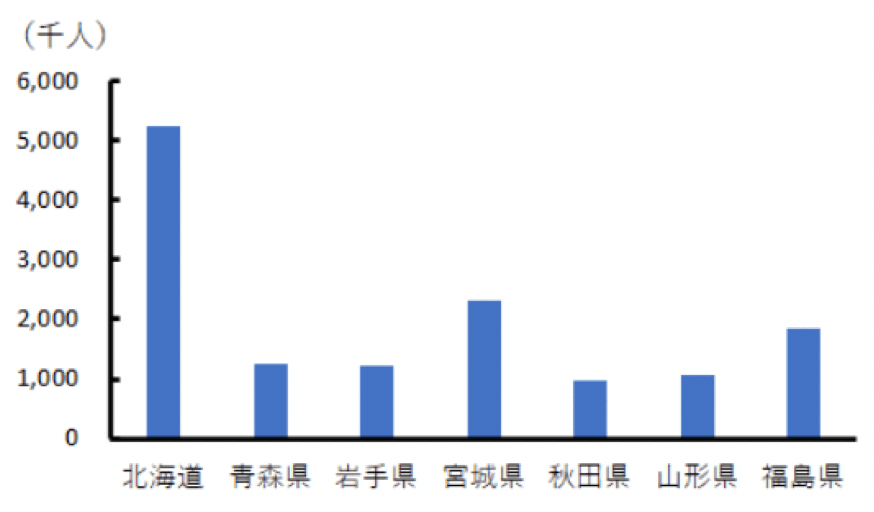
北海道・東北地方の2019年の総人口のグラフ
» 総務省統計局「人口推計(2019年(令和元年)10月1日現在)【引用】
第2表 都道府県,男女別人口及び人口性比―総人口,日本人人口(2019年10月1日現在)」
合計が100%となる構成比ではなく、さらに時系列データではなければ、棒グラフが最も分かりやすいグラフだと言えます。
データのばらつきを表す度数分布表・ヒストグラム、幹葉図、箱ひげ図
グラフには、平均値の大小などを視覚的に分かりやすく伝えるという役割があります。
しかし、グラフの役割はそれだけではありません。
$t$ 検定や分散分析といった推測統計を行うには、「データがきちんとしている(正規分布になっている)」という前提が必要です。
この「データがきちんとしている(正規分布になっている)」かは、データのばらつきをグラフに表せば確認できます。
「データがきちんとしている(正規分布になっている)」の意味が気になる人もいると思いますが、それについては「色々な分布の形~歪度・尖度~」でお話するとして、まずはヒストグラムについてお話していきます。
データのばらつき方の形が分かるヒストグラム
ヒストグラムとは、データの散らばり方がどうなっているかを表したグラフです。
縦軸に度数、横軸に階級を取ります。
例えば、以下の架空の最高血圧についての表を見てみましょう。
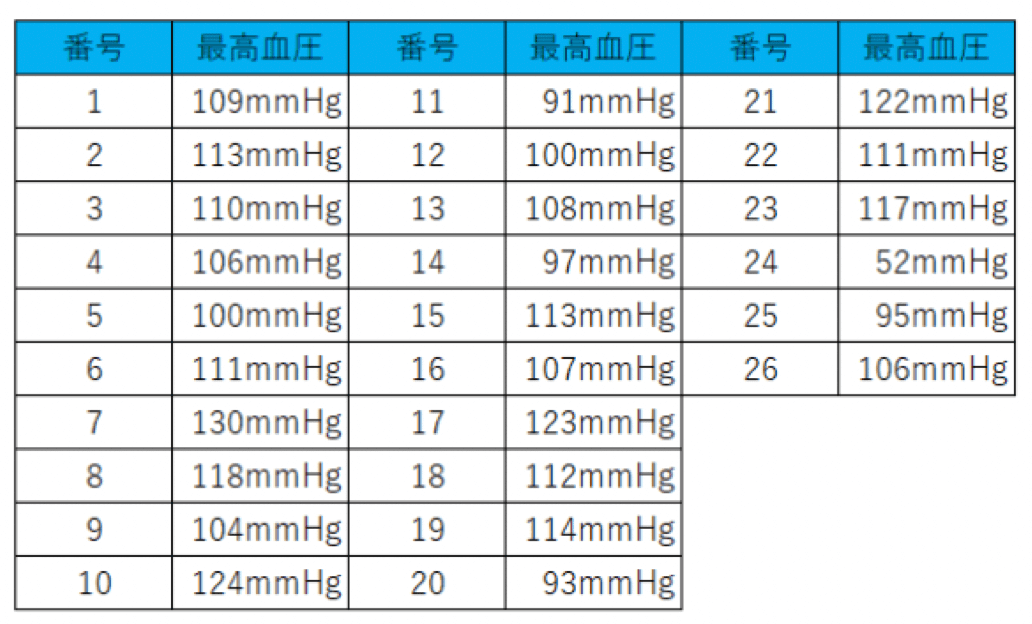
26人のデータなので、どこからどこまでの範囲か、すぐには分からないと思います。
これをヒストグラムにすると、以下のようになります。
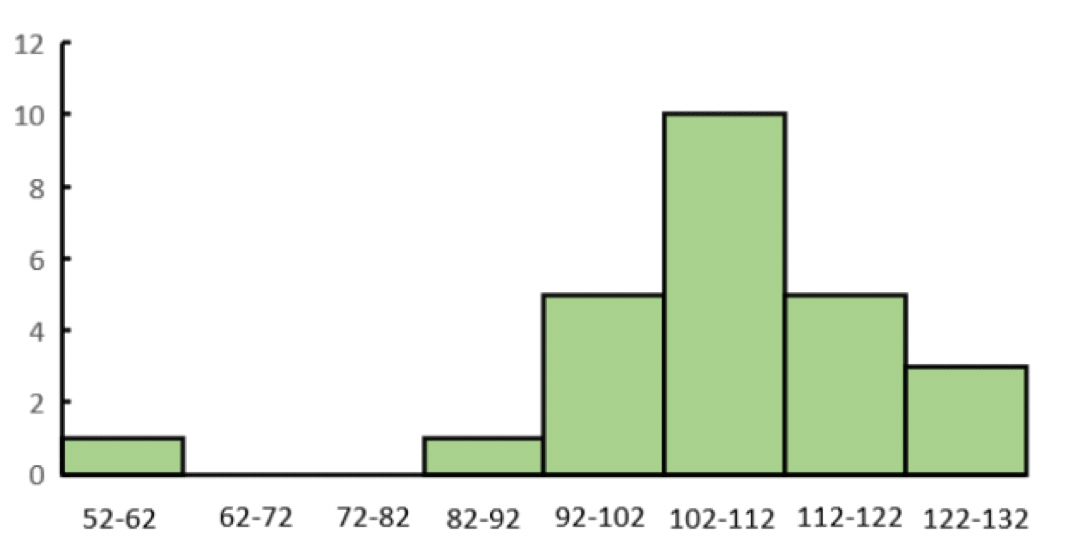
最高血圧のデータのヒストグラム
データが82~132mmHgの範囲にあることや、52~62mmHgという非常に低い最高血圧データが混じっていることが分かりました。
最高血圧が52~62mmHgの範囲というのは、健康な人ではありえない数値です。
このようなおかしい外れ値は、平均値や標準偏差を出すときに値をおかしくさせてしまう原因となります。
得られたデータについてまずヒストグラムを作ることで、このようなおかしい値がないかを直感的に確認できるのです。
52~62mmHgの範囲にあったデータ以外は、きれいな釣り鐘型をしています。
このような釣り鐘型のデータ分布は正規分布と呼ばれます。
データの値そのものを使った幹葉図
ヒストグラムと同様に、データのちらばりを表すものに幹葉図もあります。
幹葉図ではその名の通り、「幹」と呼ばれる左側と「葉」と呼ばれる右側にデータの数値を入れて視覚化します。
以下のような架空のテスト得点があるとしましょう。
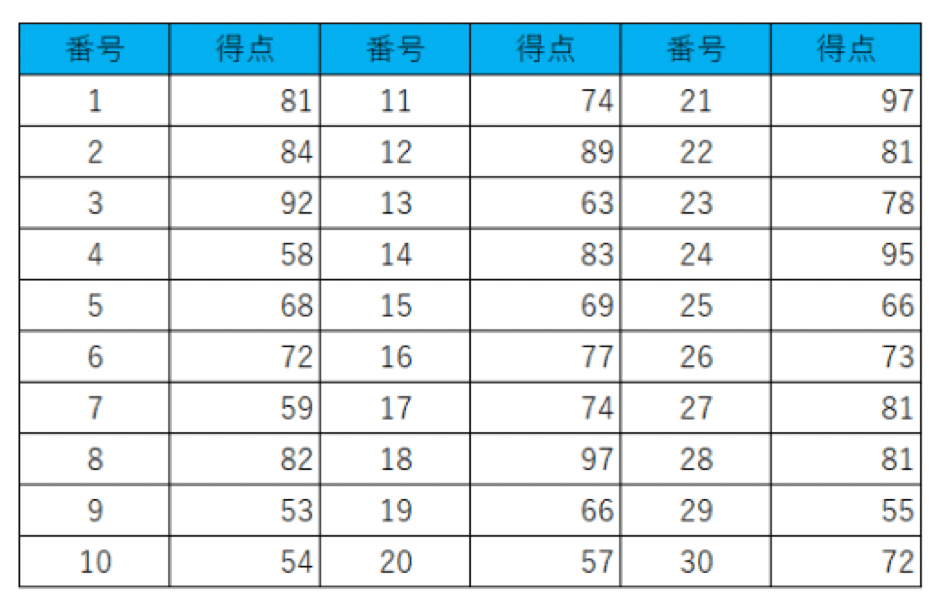
架空のテストの得点表
数字の左部分にあたる10の位を「幹」に、右部分にあたる1の位を「葉」に入れると、幹葉図は以下のようになります。
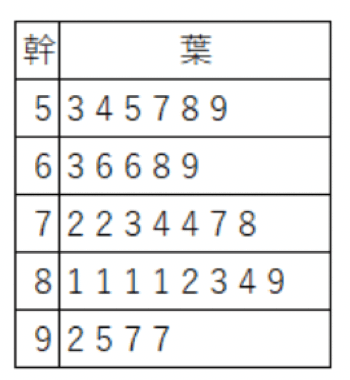
架空のテストの得点の幹葉図
同じデータでヒストグラムを作ると、幹葉図とヒストグラムで図の形がよく似ていることが分かります。
ヒストグラムを右に90°回転させると、幹葉図と同じ形ですね。
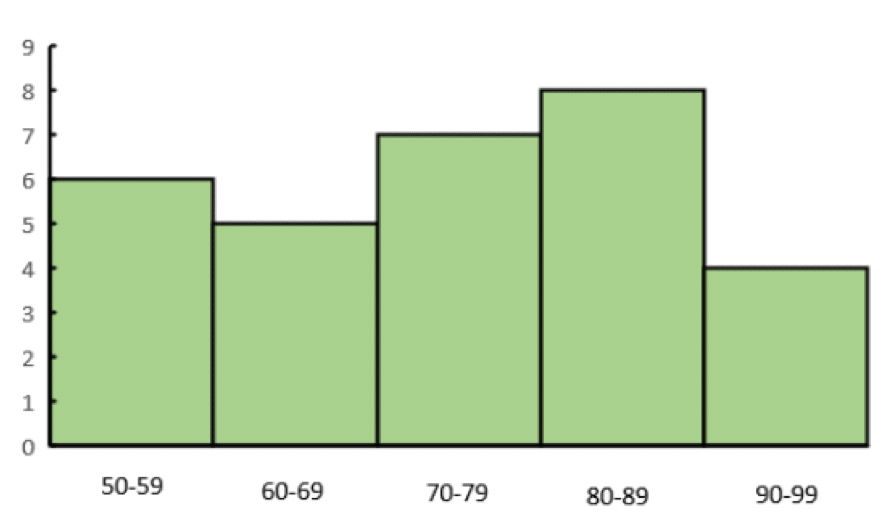
架空のテストの得点のヒストグラム
幹葉図には元のデータを維持したまままとめることができるというメリットがあります。
データの数が膨大だったり、血圧のデータのように3桁だと幹葉図を使うのは難しいですね。
その様な場合には、データの数や範囲などの条件に問題がなければヒストグラムよりも使い勝手が良いこともあります。
異なる複数のデータのばらつきを比較できる箱ひげ図
幹葉図ではあるクラスのテスト得点のばらつきを見ました。
しかし、時には複数のクラスのテスト得点のばらつきを見たいときもあると思います。
このように異なる複数のデータグループのばらつきを比較するときに用いるグラフが、箱ひげ図です。
隣のクラスのテスト得点は以下のようになったとします。
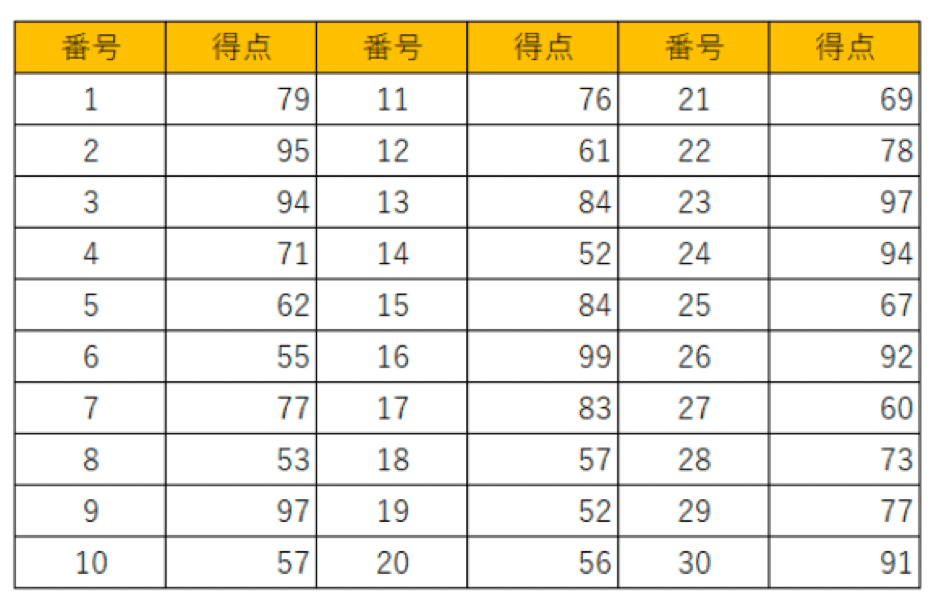
架空の隣のクラスのテストの得点
架空の元のクラスと隣のクラスのテスト得点のヒストグラムや幹葉図を作って並べてもいいのですが、それだとなかなか比較しにくいです。
しかし箱ひげ図を作ることで、以下のようにたくさんの情報を同時に比較することができます。
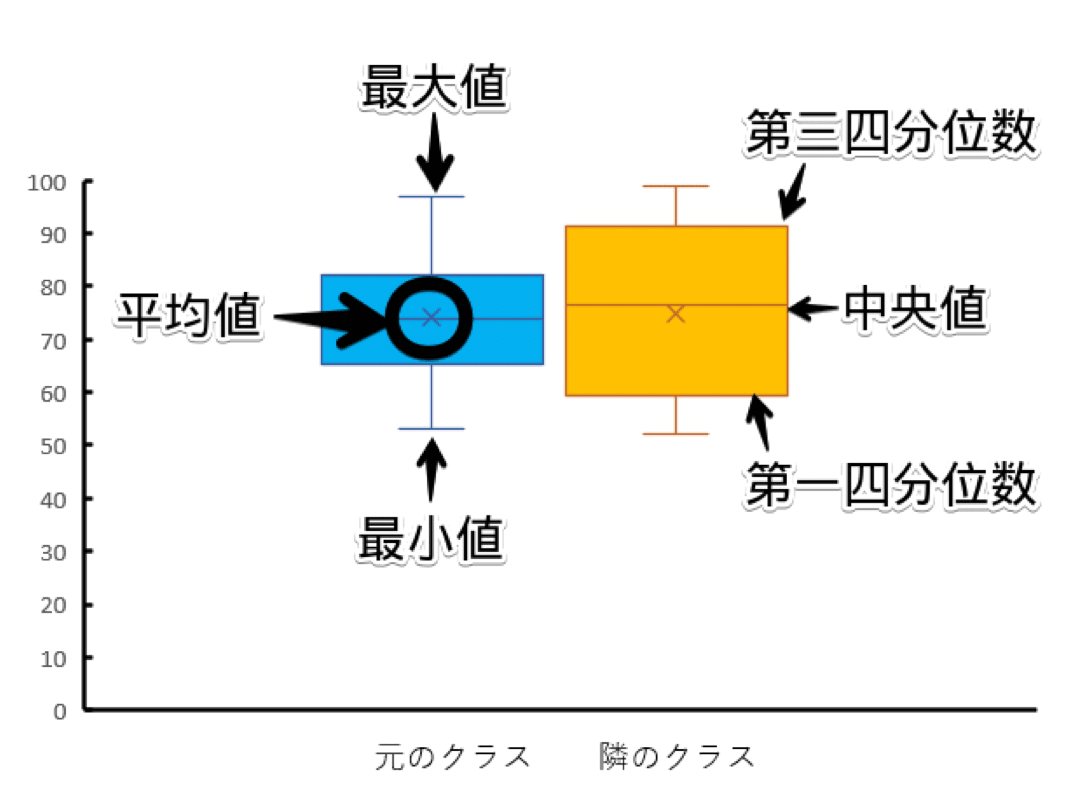
元のクラスと隣のクラスのテスト得点の箱ヒゲ図
なお、第一四分位数や第三四分位数という言葉を初めて聞いた人もいるかもしれません。
箱ひげ図でデータを四等分した値を四分位数といいます。
データを下から数えたときに25%のところが第一四分位数、50%のところが中央値、75%のところが第三四分位数となります。
色々な分布の形~歪度・尖度~
先に、得られたデータをグラフにすれば「データがきちんとしている(正規分布になっている)」かを確認できるとお話ししていたと思います。
なぜこれが大切なのかというと、血圧や心拍数といった量的変数を扱う分析は基本的に得られたデータの元の母集団が正規分布を仮定しているためです。
つまり、新しい降圧薬と従来の降圧薬の血圧に及ぼす効果を統計的に検討するt検定も、ストレスの高中低のどれが一番作業する上でよいのかを明らかにする分散分析も、得られたデータの元の母集団が正規分布していることを仮定しているのです。
これらの分析はパラメトリック検定と呼ばれます。
平均値や分散といったパラメータ(母集団の特性を示す数値)を使うことから、この名前が付けられています。
逆にいうと、量的変数でも正規分布になっていない場合があるということです。
例えば、以下は日本の所得ごとの世帯の分布 です。
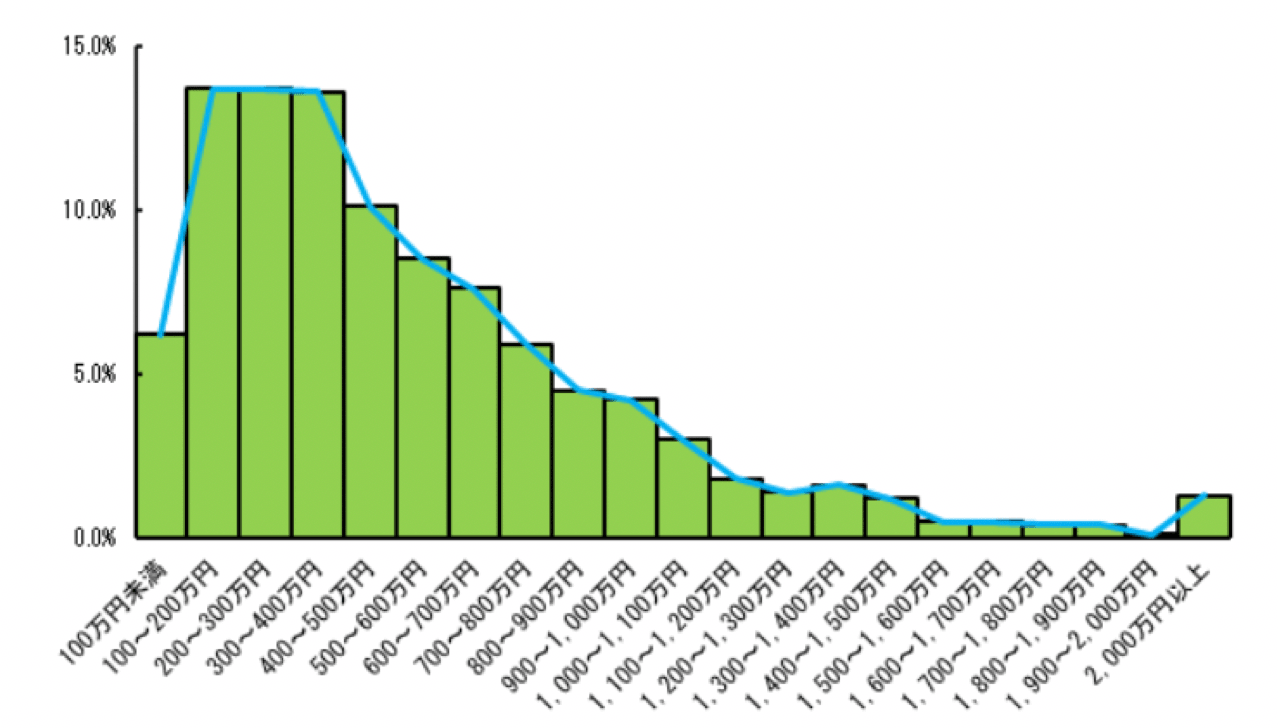
所得ごとの世帯の分布
ご覧の通り、分布の頂点が左に寄っています。
分布の頂点の位置が正規分布のときからどのくらいズレているかを歪度と言います。
分布の左右対称性を歪度は示しています。
正規分布のときが歪度は0の値を取り、上の図のように左に寄っている場合は歪度>0(つまり歪度は正の値)、逆に右に寄っている場合は歪度<0(つまり歪度は負の値)を取ります。
歪度(わいど)は以下の式から求めることができます。
$$\frac{n}{(n-1)(n-2)} \sum_{i=1}^{n}\left(\frac{x_{i}-\bar{x}}{s}\right)^{3}$$
- $n$:サンプル数
- $x_{i}$:各データの値
- $\bar{x}$:$x_{i}(i: 1,2, \cdots, n)$の平均値
- s:標準偏差
また、分布が正規分布になっていないということは、分布の頂点が左あるいは右に寄っているということだけではありません。
例えば、以下の架空の模試得点のデータがあります。
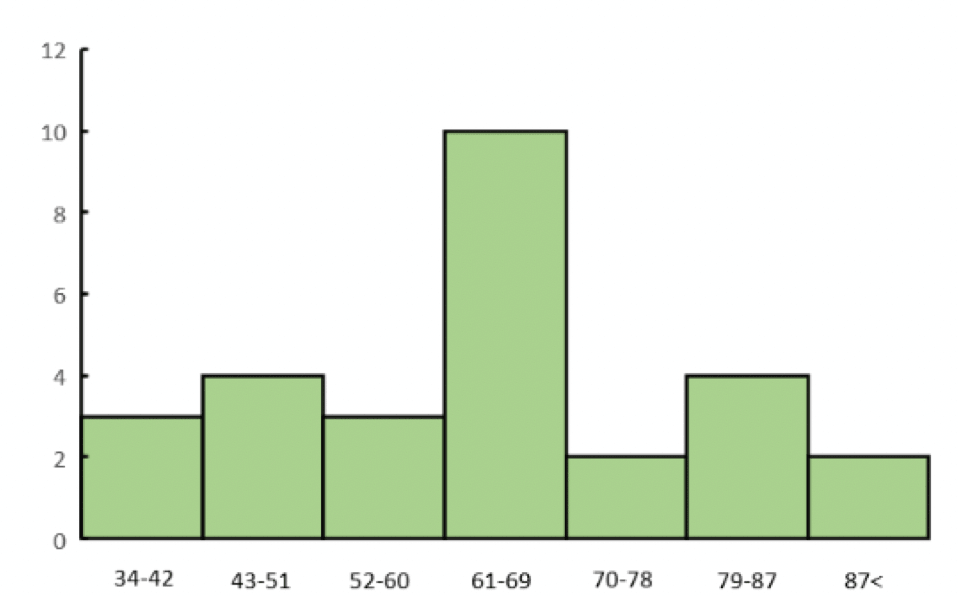
架空の模試得点
真ん中に頂点がありますが、正規分布の釣り鐘型と比べると頂点にデータが集中する尖った形になっていることが分かると思います。
このような分布が正規分布と比べてどのくらい尖っているかあるいは広がっているかを示す指標を尖度と言います。
尖度(せんど)の値は、正規分布の場合は0となり、上の図のように頂点が尖っている場合は尖度>0(つまり尖度は正の値)となります。
逆に頂点があまり目立たない平ぺったい形になっている場合は尖度<0(つまり尖度は負の値)となります。
尖度は以下の式から求めることができます。
$$\frac{n(n+1)}{(n-1)(n-2)(n-3)}$$
$$× \sum_{i=1}^{n} \frac{\left(x_{i}-\bar{x}\right)^{4}}{s^{4}}-\frac{3(n-1)^{2}}{(n-2)(n-3)}$$
- $n$:サンプル数
- $x_{i}$:各データの値
- $\bar{x}$:$x_{i}(i: 1,2, \cdots, n)$の平均値
- s:標準偏差
変数と変数の関連性~散布図~
データのちらばりを見るということは、1種類のデータがどんな分布をしているかというだけではありません。
実は、2種類のデータのちらばりに関連があるかということも見ることができます。
例えば、以下のような架空の身長・体重のデータがあったとします。
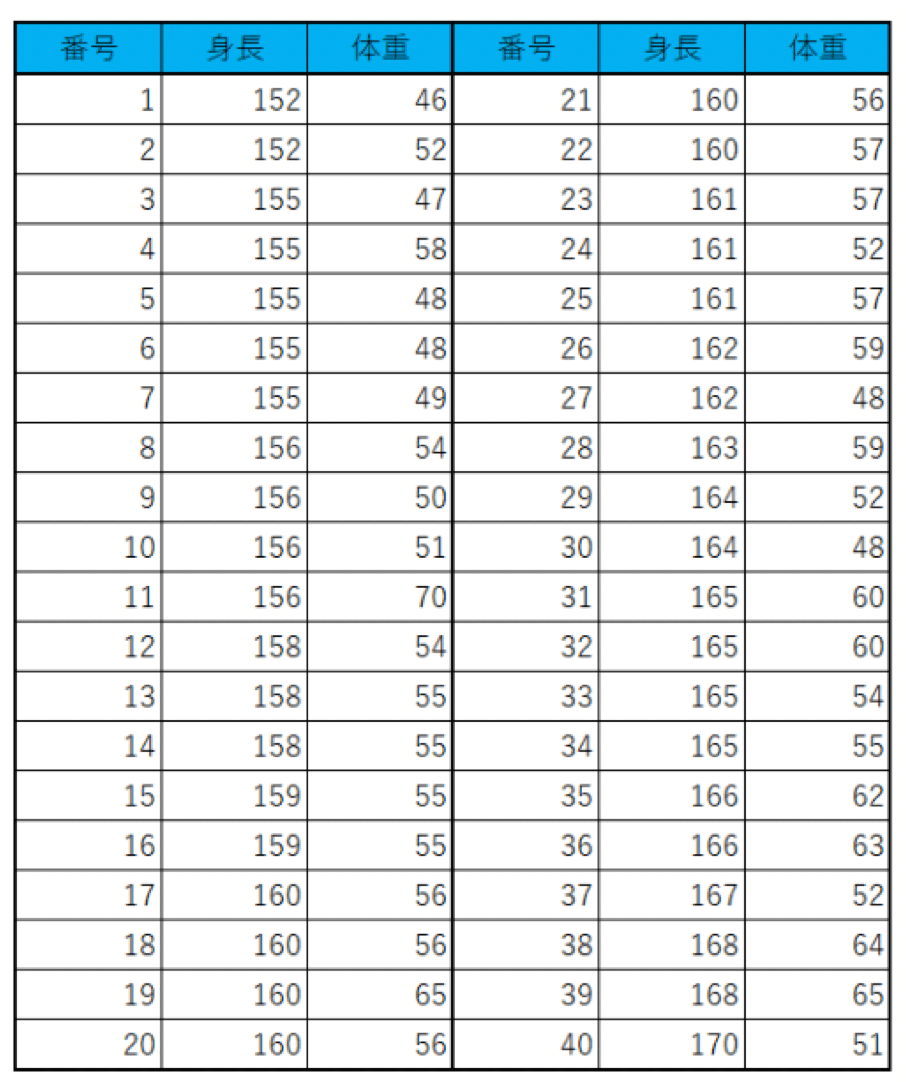
架空の身長・体重のデータ
このデータを、右軸を体重、左軸を身長とする枠の中にプロットすると、以下の図ができあがります。
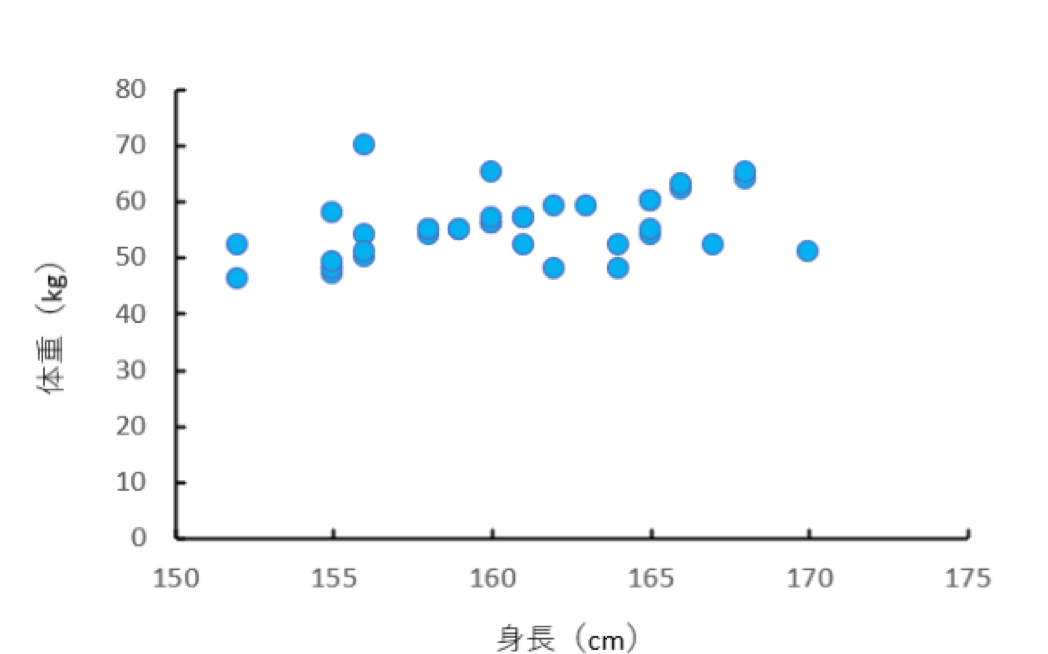
架空の身長・体重のデータの散布図
この図を散布図と呼びます。
この図をじっと見ていると、身長と体重に以下のような直線関係があることが見えてきます。
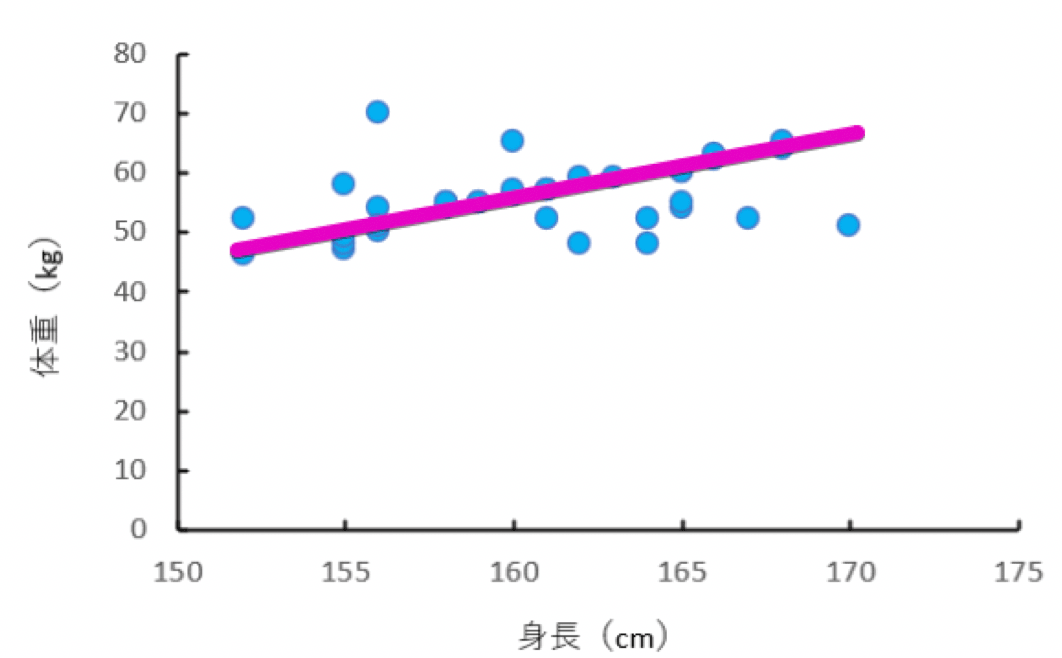
架空の身長・体重のデータの散布図
このデータとデータの間の関連を相関と言います。
詳しくは、10講座目の相関分析でお話ししますので、今は散布図というものがあることを覚えてもらえれば大丈夫です。
質的変数も実はグラフが作れる~度数分布表・度数分布図・2元クロス表~

ここまでは量的変数のグラフを見てきました。
しかし、名義尺度や順序尺度といった質的変数でもグラフを作ることができます。
例えば、名義尺度の度数分布表は以下のようになります。
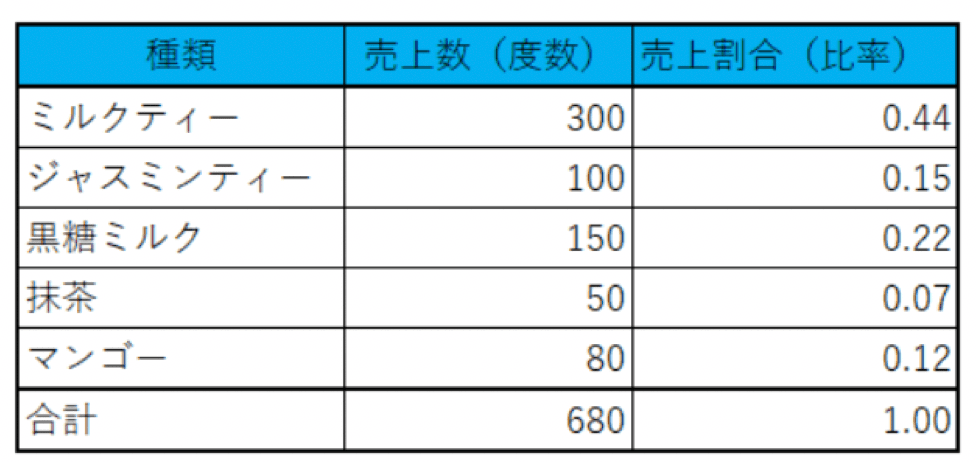
架空のタピオカミルクティーの売上げの度数分布表
このデータを元に、以下のような棒グラフを作って視覚化することもできます。
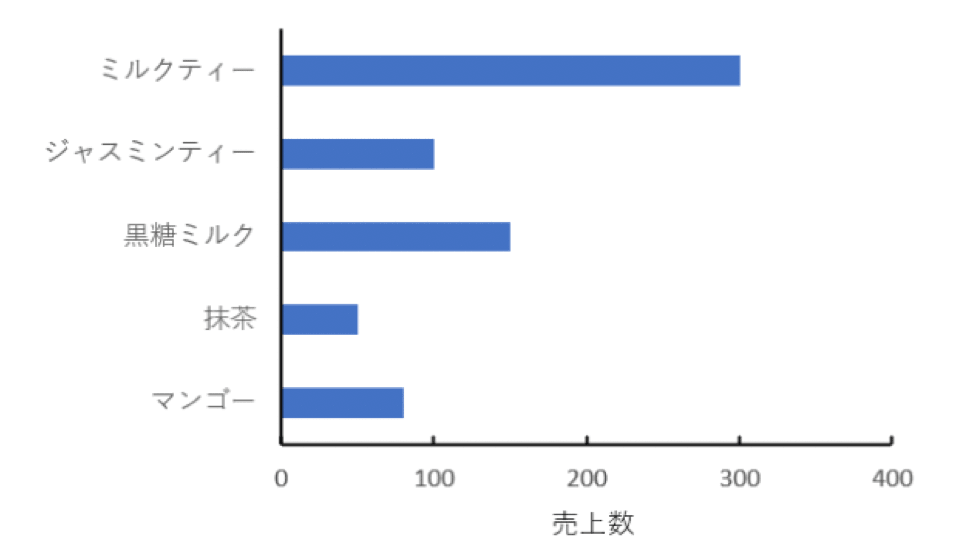
架空のタピオカミルクティーの売上げの棒グラフ
量的変数では2つのデータの関連性を散布図を使って見ることができましたが、質的変数でも2元クロス表を使えば2つのデータの関連性を見ることができます。
例えば、以下は年代ごとのタピオカミルクティーの売上データです。
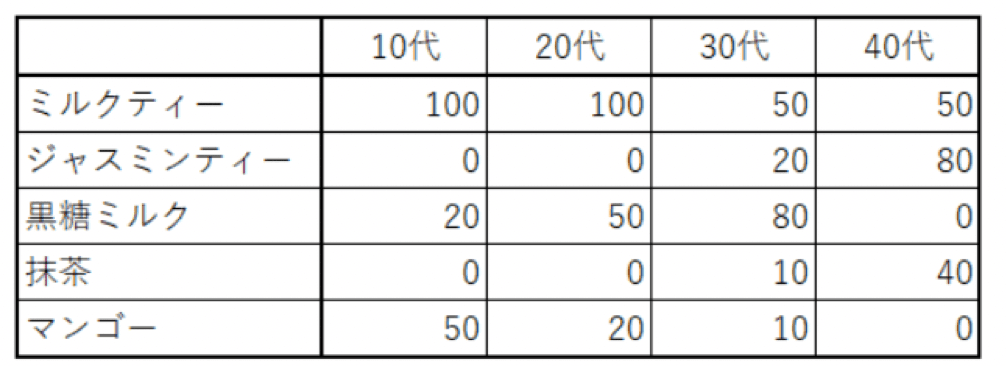
年代ごとのタピオカミルクティーの売上データ
最初の全体でのデータではミルクティーが一番売上が高かったですが、二元クロス表を見てみると30代では黒糖ミルクのほうがミルクティーよりも売上が良いですね。
さらに、40代が他の年代と比べジャスミンティーや抹茶の売上に貢献していることなどが分かります。
まとめ|練習問題
まとめとして、今回学習した内容を踏まえて、練習問題を作成しましたので1つ1つ確認してみましょう。
問題の概要は以下の通りです。
- 問題①:箱ひげ図
- 問題②:散布図
- 問題③:ヒストグラム
- 問題④:ローレンツ曲線のジニ係数
では早速、問題を解いていきましょう。
問題① 箱ひげ図
次の箱ひげ図は1990年~2020年1月の東京の最低気温データです。
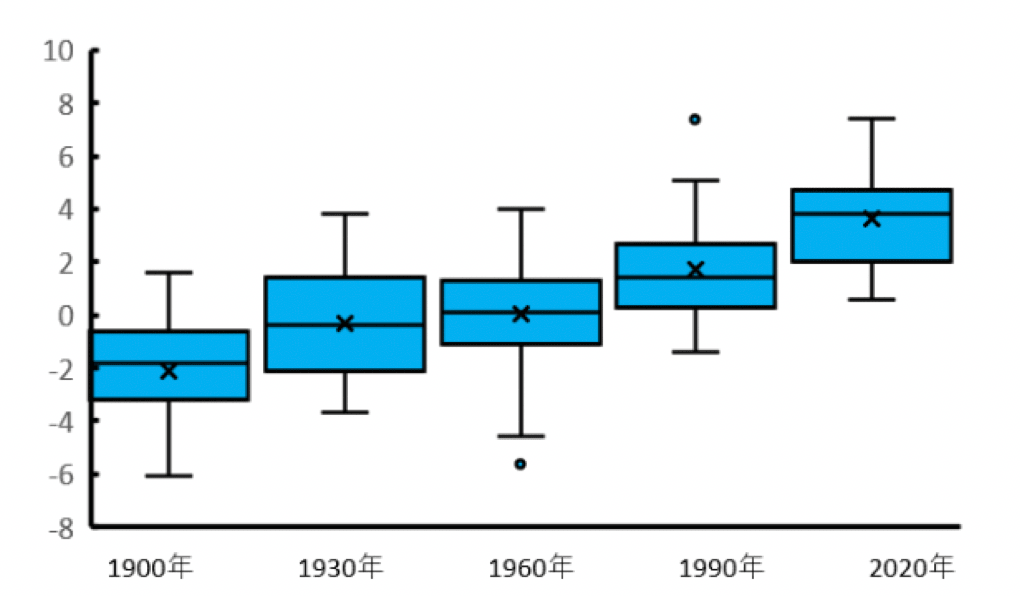
1月の東京の最低気温
次の表は、1月の東京の最低気温の箱ひげ図を基に作った度数分布表です。
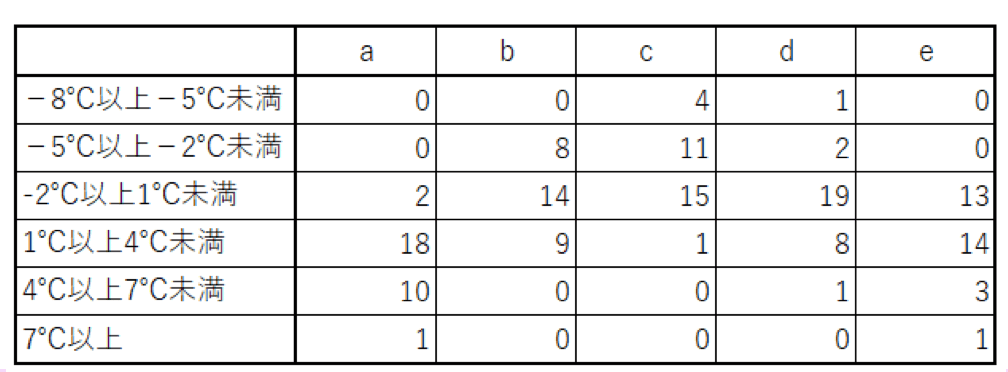
資料:気象庁「気象観測データ」
問:1960年はa~eのどれでしょうか。
解説:この手の問題は、消去法で丁寧に考えていくと分かりやすいです。
1960年は6℃以上のデータはありませんので、aとeは違います。
気温が高いのは1990年と2020年なので、aとeはそれらでしょう。
b~dで見ていくと、bだけ-8℃以上-5度未満が1つもありません。
1900年、1930年、1960年の中で最低気温の最小値が-4℃以上と比較的高い1930年がbに該当します。
残りはbとdのどちらかが1960年になることになります。
bとdで違いを見ていくと、bのほうが-5℃以上-2度未満と最低気温が低め、dでは1℃以上4℃未満が8個と最低気温が高めなのが分かります。
残った1900年と1960年では1960年のほうが箱ひげ図が全体的に最低気温のデータが高めであることが読み取れるので、dが1960年になることが分かります。
なお、箱ひげ図関連の問題は2019年11月、2018年11月と比較的出題されやすいので、押さえておきましょう。
問題② 散布図
次のデータは都道府県の道路交通事故件数と道路の舗装率の散布図です。
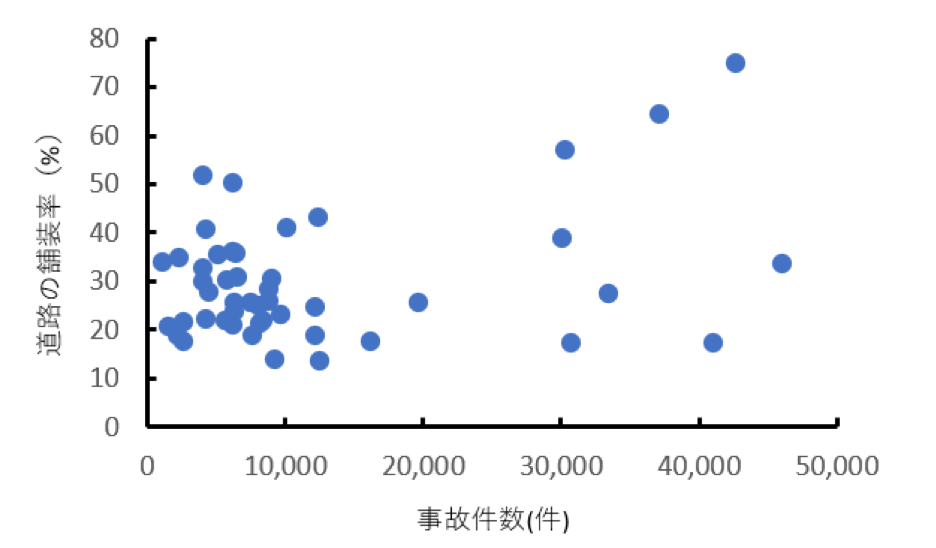
資料:総務省統計局Webサイト「なるほどデータforきっず」の「おやくだちデータ倉庫」内の都道府県別データ
問題:散布図から分かることを以下のa~eの中から選んでください。
a: ほどんどの都道府県で事故件数は30,000件以上となっている
b: 事故件数が40,000件数以上の都道府県は3つである
c: 交通事故件数の分布は滑らかな正規分布となっている
d: 道路の舗装率が50%以上の都道府県がほとんどである
e: 道路の舗装率が低いほど、事故件数多い
解説
「a ほどんどの都道府県で事故件数は30,000件以上となっている」は誤り。事故件数が30,000件以上の都道府県は8つなので。
「b 事故件数が40,000件数以上の都道府県は3つである」は正しい。
「c 交通事故件数の分布は滑らかな正規分布となっている」は誤り。事故件数は0~20,000件で特に多く、30,000件~50,000件で8件なので、2極化している傾向にあるため。
「d 道路の舗装率が50%以上の都道府県がほとんどである」 道路舗装率が50%以上の都道府県は5件なので、誤り。
「e 道路の舗装率が低いほど、事故件数多い」以下の図の通り道路舗装率が高いほど事故件数は高い傾向にあるので、誤り。
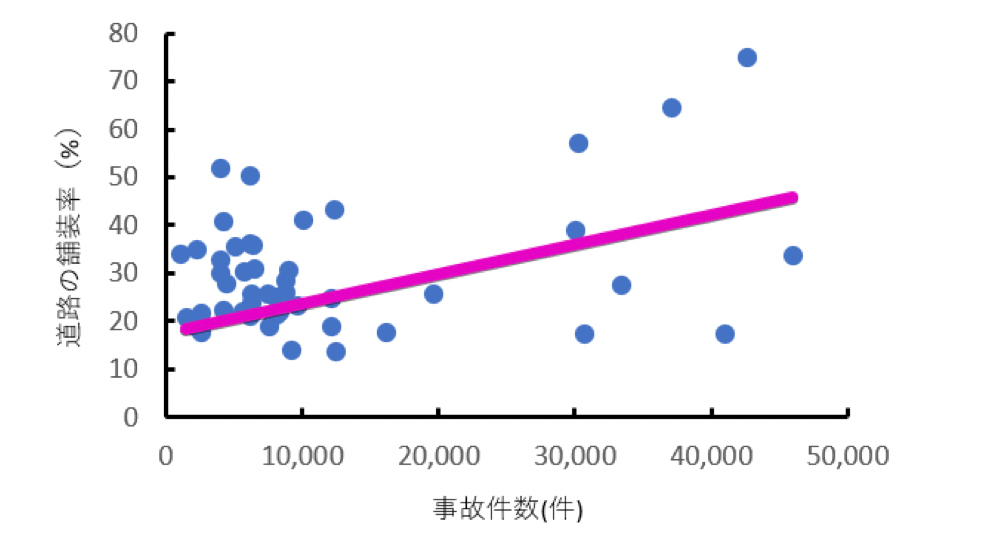
道路舗装率が高いほど事故件数は高い傾向にある
よって、答えはb。
散布図の問題は2019年6月、11月、2018年6月と結構出題されていますので、必ず押さえましょう。
問題③ ヒストグラム
次のデータは日本の所得ごとの世帯の分布です。
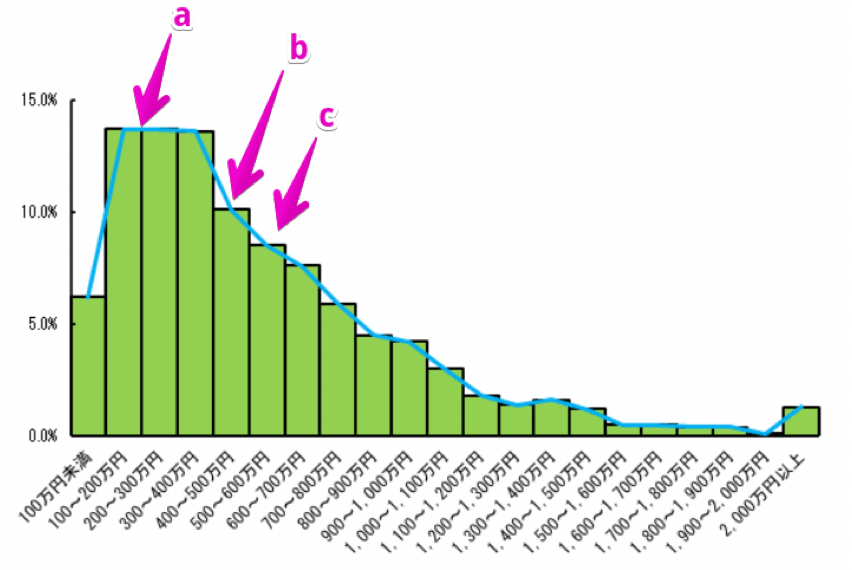
所得ごとの世帯の割合 » 厚労省の平成 30 年 国民生活基礎調査の概況より【引用】
問題:a~cは平均値、中央値、最頻値のどれにあたりますか?
解説:右に裾が長い形のヒストグラムの場合は、一般に最頻値<中央値<平均値の関係が成り立ちます
よって、aは最頻値、bは中央値、cは平均値となります。
なお、同じような問題は2016年11月の試験で出題されました。
問題④ ローレンツ曲線のジニ係数
以下の架空のデータのローレンツ曲線のジニ係数を求めてください。
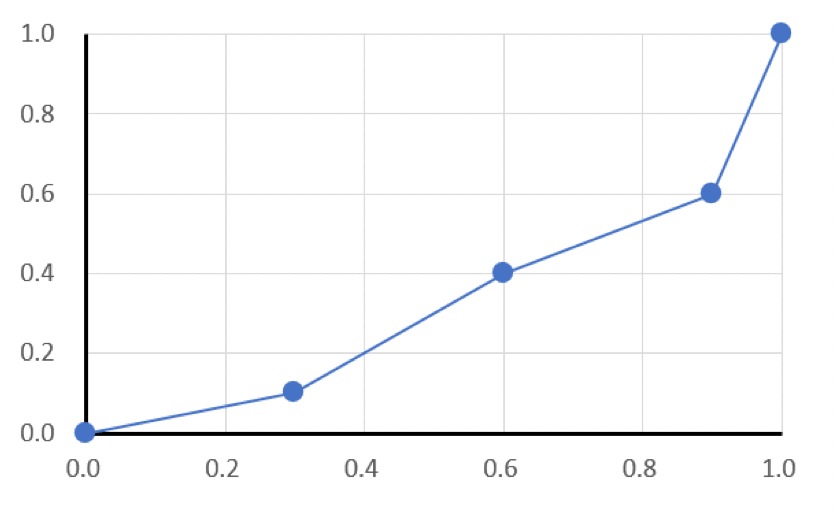
ジニ係数は、以下のピンク枠の三角形から黄緑色の三角形1と台形2~4を引けば産出できます。
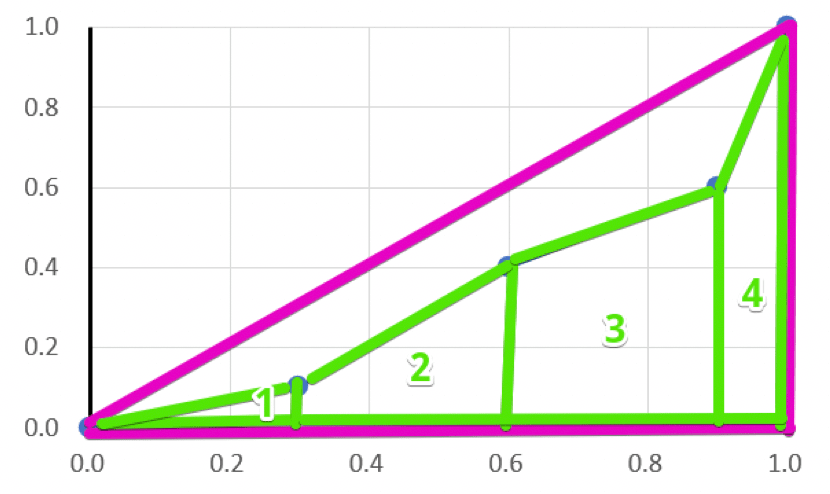
- ピンク色の三角形の面積:$1.0×1.0×0.5=0.5$
- 黄緑色の三角形1の面積:$0.3×0.1×0.5=0.015$
- 黄緑色の台形2の面積:$(0.1+0.4)×0.3×0.5=0.075$
- 黄緑色の台形3の面積:$(0.4+0.6)×0.3×0.5=0.15$
- 黄緑色の台形4の面積:$(0.6+1.0)×0.1×0.5=0.08$
よって、
$0.5-0.015-0.075-0.15-0.08=0.18$となります。
なお、ジニ係数を求めるという問題は2018年6月に出題されました。
今回は以上となります。
