【機械学習】回帰木・決定木で予測モデルを作成する【手順あり】

機械学習のアルゴリズム(予測モデル)にはいくつか種類があります。

例えば、線形回帰やランダムフォレスト、回帰木、決定木などがあります。

今回は予測モデルの中でも教師あり学習のうち、回帰（分類でも用いられる）で使用される、回帰木・決定木を用いた予測モデルの作成方法について、具体的な例を用いつつ解説していきます。

決定木→回帰木の流れで解説していきます。では早速見ていきましょう。

回帰木・決定木とは

何かを分類する際にYesかNoかで場合分けを行い、分類することがありますね。

決定木はこの分類の過程のなかで、最初の状態からYes/Noの選択肢によって次々に枝分かれしていくように見えるため、決定木モデル（decision tree）と呼ばれます。

ここでは決定木モデルの説明を行うために以下の例を使用します。

ある通販サイトがあるとします。
前の月のサイトのクリック数(訪問数)、前の月のサイトの購入金額、今月(当月)のサイトを解約したかどうか(解約=1,継続=0 と設定します)のデータがあります。これらのデータから、サイトの会員の解約を予測するモデルを作って行くことを考えます。

まずは、データから散布図を描いてみましょう。

データの散布図を描く

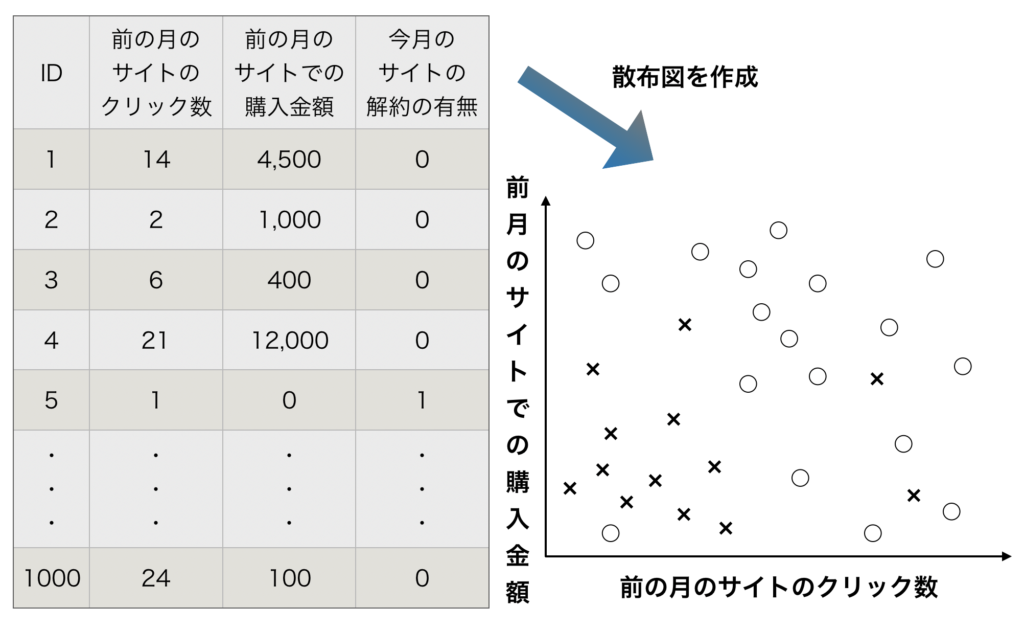
データの散布図を描くと上の様な図になります。

前の月の訪問者数が少なく、また前の月の購入金額が少ないと、今月(当月)の解約の数が増えていくのがわかります。

次に右側の散布図についてですが○と×をなるべく分けるために線を加えて分類しよう！

というのが決定木の基本コンセプトです。

実際に赤線を加えて○と×を分けてみましょう。

決定木一本目

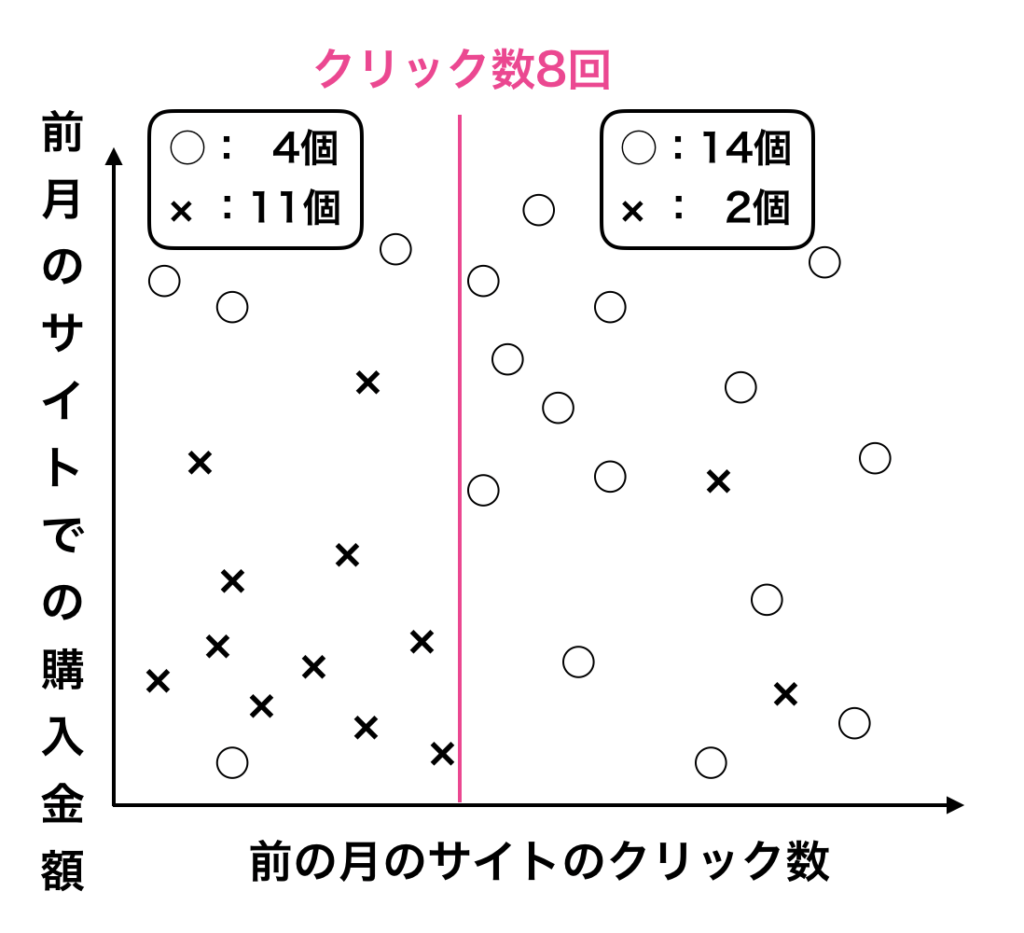
赤線を一本引くことで、○と×をなるべく分ける様に工夫してみました。

決定木において重要なことは、「○と×をなるべくうまく偏らせる様に線を引いて分ける」ということにあります。

決定木に一本目の線を加えることで○と×をよい感じに分ける事ができました。

左側は×の個数が11個と「×の純度」をあげる事ができました。

要するに目的関数は純度になるわけです。

さらに純度を上げるためにもう一本線を引いてみましょう。

目的関数とは

目的関数：目的関数値とは機械学習アルゴリズムが何を最小化したいのか、最大化したいのかを表現するものです。

決定木2本目

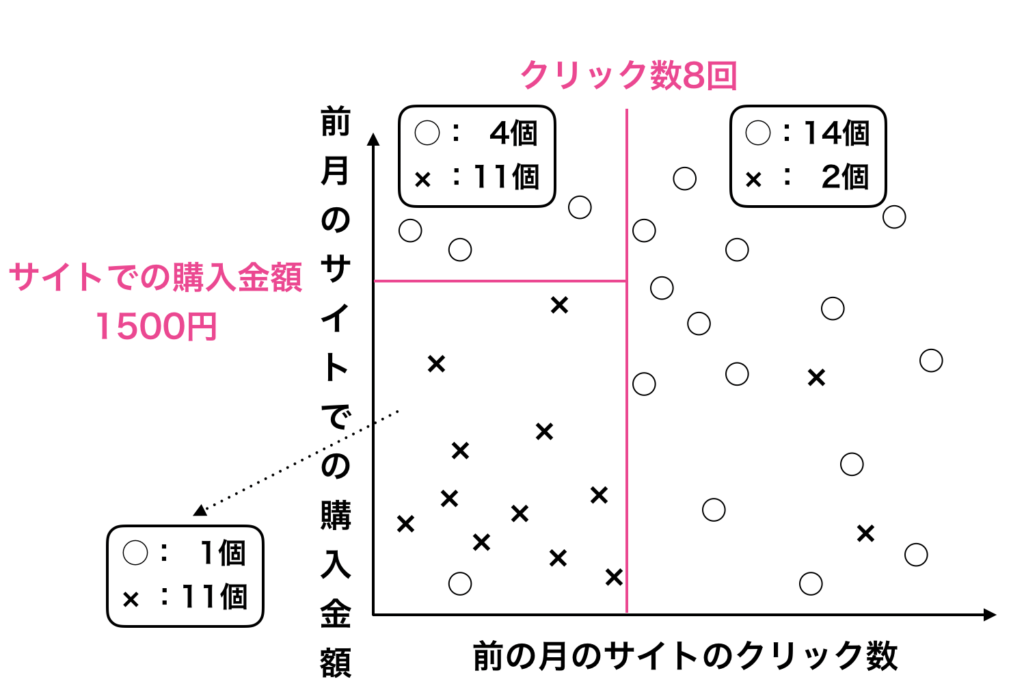
さらに一本の決定木の線を加える事で、左下の区画では○が1個、×が11個になり、×の純度が上がった事が分かります。

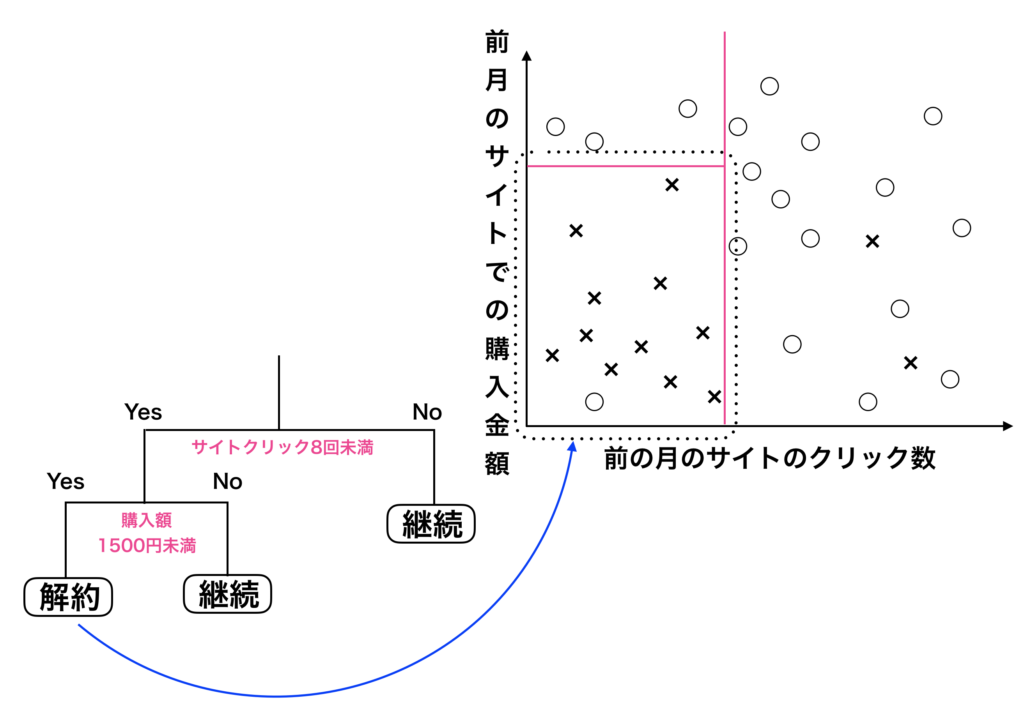
これは左下の区画が「前月のサイトのクリック数が8回以下で、前月のサイトでの購入金額が1500円以下なら解約し安い」という事を意味します。

逆に左上の区画は「前月のサイトのクリック数が8回以下で、前月のサイトでの購入金額が1500円以上なら解約しにくい」という事も意味しています。

この様に、決定木は横線や縦線を加えて条件を絞る事で表現する事ができます。このことを「If-Thenルール」と呼ぶことがあります。

また、この様な直線を引くことはIf -Thenのツリーを利用した場合分けをする事もできます。

今まで線を加えて表現してきた条件をツリーで表現してみましょう。

ツリーと散布図の対応関係を把握する。

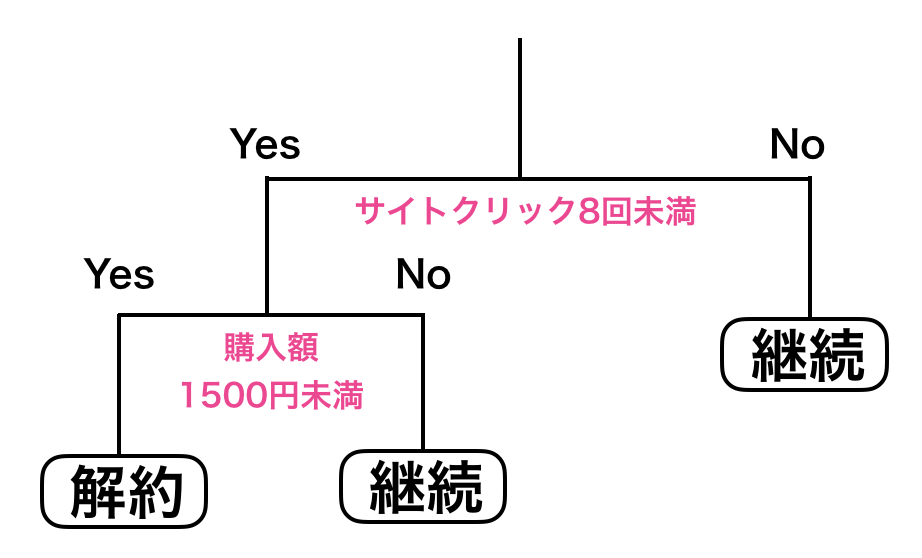
ここで、機会学習にはハイパーパラメーターと呼ばれる機会学習アルゴリズムを決定するパラメーターがあります。

このパラメーター自体は分析を行う者が決める事なのですが、この決定木ではどれがハイパーパラメーターになるでしょうか。

決定木におけるハイパーパラメーターは「Yes/Noの場合分けによるツリーの深さ」です。

ツリーの深さが深ければ深いほど、純度が良くなり、ターゲット変数に当たる可能性が高くなります。

しかし、この決定木は前月のサイトの訪問回数とサイトで購入下金額を今月(当月)分に適応させたものです。

今後必ずこの分類が使えるとは限りません。この様に今月しか使えないルールを作ることを「過学習(オーバー・フィッティング)」と言います。

今までの流れからもわかる様に、決定木は過学習が起きやすいですので、ツリーの深さをうまく調整し過学習がなるべく起きない様にコントロールする必要があります。

メモ

ターゲット変数とは、教師あり学習の機械学習において予測した対象となる変数のことをさします。

回帰木・決定木で予測モデルを作成する際のポイント

機械学習アルゴリズムを理解する上では(特に教師あり学習のアルゴリズム)、以下の5つのポイントがあります。

目的関数
関数の形状
ハイパーパラメーター
モデルの解釈可能性と予測性能(精度)
予測したい対象の変数(ターゲット変数)：連続値やフラグ

この5つのポイントについて、決定木・回帰木では以下の様に表現する事ができます。

予測したい対象の変数(ターゲット変数)：クラス
目的関数：純度
関数の形状：ツリー(If-Thenルール)
ハイパーパラメーター：木(tree)の深さ
モデルの解釈可能性と予測性能(精度)：解釈の可能性は高い一方で、予測性能はそれほど高くはない。

次に回帰木の要点について見ていきましょう。

回帰木の要点

予測したい対象の変数(ターゲット変数)：連続値
目的関数：分散
関数の形状：ツリー(If-Thenルール)
ハイパーパラメーター：木(tree)の深さ
モデルの解釈可能性と予測性能(精度)：解釈の可能性は高い一方で、予測性能はそれほど高くはない。

回帰木も決定木とはそれほど変わりません。

ほとんど同じと考えてよいでしょう。

異なる点としては、ターゲット限数をクラスではなく、連続値として、それに伴って目的関数も純度ではなく、それぞれの区画におけるターゲット変数の分散になります。

機械学習における決定木の実装方法【scikit-learn】

決定木を使う場合、通常は scikit-learn の sklearn.tree.DecisionTreeClassifier を利用すればOKです。

参考：sklearn.tree.DecisionTreeClassifier

ここでは、統計学者のR. A. フィッシャーが用いたアヤメの分類データセットを使用しますので、以下のコードを実行するフォルダと同じフォルダにデータをダウンロードしてください。

なお、irisデータセットは、sklearn.datasetsから取ってくることができます。

In[] ①

# ライブラリの読み込み
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_validate

# ライブラリの読み込み

from sklearn.tree import DecisionTreeClassifier

from sklearn.model_selection import cross_validate

In[] ②

from sklearn import datasets
iris = datasets.load_iris()

1 2	from sklearn import datasets iris = datasets.load_iris()

Out[] ②

data
target
target_names
DESCR
feature_names

data

target

target_names

DESCR

feature_names

In[]③

print(iris['DESCR']) # description:説明

1	print(iris['DESCR']) # description:説明

Out[]③

ここで、データはdata（入力特徴量として使える属性データ）とtarget（分類されたアヤメの種名）とに分かれています。

In[] ④

iris['data'].shape

1	iris['data'].shape

Out[] ④

(150, 4)

(150, 4)

In[] ⑤

iris['target'].shape

1	iris['target'].shape

Out[] ⑤

(150,)

(150,)

In[] ⑥

set(iris['target'])

1	set(iris['target'])

Out[] ⑥

{0, 1, 2}

{0, 1, 2}

In[] ⑦

iris[ 'target_names']

1	iris[ 'target_names']

Out[] ⑦

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

1	array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

In[] ⑧

# 訓練に使うデータを用意
values = iris['data'][:,2:]
labels = iris['target']

# DecisionTreeClassifierを作成
dtc = DecisionTreeClassifier(criterion='gini', splitter='best', random_state=1)

# 5-交差検証
dtc_cv = cross_validate(dtc, values, labels, cv=5)

# 正答率を表示
dtc_cv['test_score'].mean()

# 訓練に使うデータを用意

values = iris['data'][:,2:]

labels = iris['target']

# DecisionTreeClassifierを作成

dtc = DecisionTreeClassifier(criterion='gini', splitter='best', random_state=1)

# 5-交差検証

dtc_cv = cross_validate(dtc, values, labels, cv=5)

# 正答率を表示

dtc_cv['test_score'].mean()

Out[] ⑧

0.9533333333333334

1	0.9533333333333334

質問が多く、初心者の方がつまづき安いコードの解説を行なっていきます。

values = iris[‘data’][:,2:] これはirisのdataのうち、150個のデータとpetal length、petal widthの2つだけを説明変数として用いてたい、ということでこの2つのデータを iris[‘data’] からスライスで取り出しています。iris[‘data’] の行は全て、列は3,4列目ということで [:, 2:] としています。
dtc = DecisionTreeClassifier(criterion=‘gini’, splitter=‘best’, random_state=1) についてです。

ここでは決定木を行なっており、'gini' とありますが、クロスバリデーション(交差検証)を行なっているわけではありません。

'gini' は分割の基準としてジニ係数を用いるということを意味しています。

'splitter' は、どこの変数でyes/noを分けるか、の方法を指定するハイパーパラメータです。

sklearnではデフォルトで 'best' になっていますので、実はこの記載は必要ありません。

'best' では、一番影響力のありそうな変数から 'split' していきます。他にはrandomという指定ができますが、こちらはランダムに変数を選びます。

random_state は乱数を制御するパラメータを意味します。

None にすると毎回違うデータが生成されますが、整数を種として渡すと毎回同じデータが生成されます。

random_state を指定すると、同じ乱数を発生させることができるわけです。

乱数を用いた場合に毎回本当に乱数が出てきては再現性が確認できず困ることがあります。

ですので再現性を担保する目的として、乱数の種を指定するために random_state を設定しています。

この数字が同じであれば、何度実行しても同じ値が出てきます。
» sklearn.model_selection.train_test_split
dtc_cv = cross_validate(dtc, values, labels, cv=5) の cv=5 は何を表しているのでしょうか。

CVはクロスバリデーション(交差検証)の数です。何個にデータを分けて test data として回していくか、という数です。

引数の数については、cross_validate関数を公式サイトで確認すると良いでしょう。

cross_validation の引数を指定しなければならないパラメータは、“y=None”のように引数の所にイコールで指定がなかった場合にとる値が入っています。

これがない引数はこちらで与えてあげないと動きません。公式サイトをみると、最初の2つだけで何とか動くようですね。