こんにちは。産婦人科医のとみー(twitter:@obgyntommy)です。
この記事では具体的なワインのデータを用いて、機械学習のうち教師なし学習の一通りの流れを学びます。
今回学習する、機械学習のうち教師なし学習の一般的な流れは以下の通りです。
教師なし学習の機械学習の流れ
- データの内容の確認
- データの前処理
- Feature Scaling
- 次元削減
- 教師なし学習(クラスタリング)数の決定
- 教師なし学習(クラスタリング)
- 結果の解釈
Google Colaboratory でコードを動かす事も出来ますので、記事で学習するのが大変な方はこちらのリンクをご参照下さい。
scikit-learnを用いた機械学習の流れについては、以下の記事を参照して下さい。
-

【機械学習】scikit-learnの使い方【基礎から全て解説】
続きを見る
Google Colaboratoryの使い方については以下の記事を参照して下さい。
-

Google Colaboratoryの使い方【完全マニュアル】
続きを見る
尚、ワインのデータセットを用いた教師ありの機械学習についてはこちらの記事をご参照下さい。
-

【教師あり学習】機械学習でワインの品質判定を行ってみよう【scikit-learn】
続きを見る
それでは早速学習していきましょう。
ワインのデータセットの読み込みとデータ内容の確認

skleanのライブラリから「wine」のデータセットを読み込みます。
wineのデータセットは典型的な多値分類のデータセットです。
アルコール量やマグネシウム量などの成分のデータから、3種類のワインの分類を行うためのデータセットになります。
ワインのデータセットの中身を確認してみましょう。
In[]
1 2 3 | from sklearn.datasets import load_wine data_wine = load_wine() data_wine |
Out[]

このデータセットの中身はpythonの辞書型になっていますので、以下のように取得したい対象のキーを指定しましょう。
そうする事で、対象の中身(バリュー)を取得できます。 例えば以下のコードでは正解ラベルの取得を行なっています。
辞書型の復習
Pythonの辞書型が身についていない方はこちらの記事を復習しましょう。
-

【python】辞書の作り方【基本から応用まで】
続きを見る
In[]
1 | data_wine["target"] |
Out[]
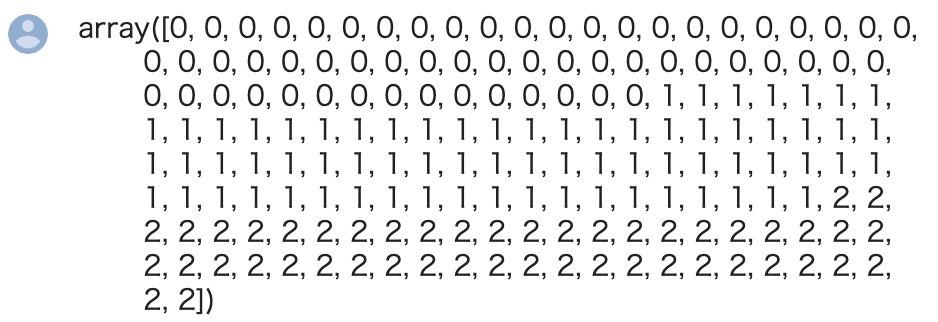
データの前処理

今回は教師なし学習がテーマですので、正解ラベル(上の data_wine["target"])は考慮しません。
教師学習とは何かというと、『正解ラベル無しで特徴量のみでデータを分類する』ことになります。
よって特徴量のみをデータセットとし、それの前処理を行います。特徴量の名前はfeature_names、値はdataキーに含まれていますのでそれを用います。
また、教師なし学習は予測精度の評価ができないので、全てのデータをトレーニングデータとして扱います。
In[]
1 2 3 | import pandas as pd train = pd.DataFrame(data_wine["data"],columns=data_wine["feature_names"]) train.head() |
Out[]

describeメソッドによって、一括で全ての特徴量の統計値の概要を表示できます。
In[]
1 | train.describe() |
Out[]
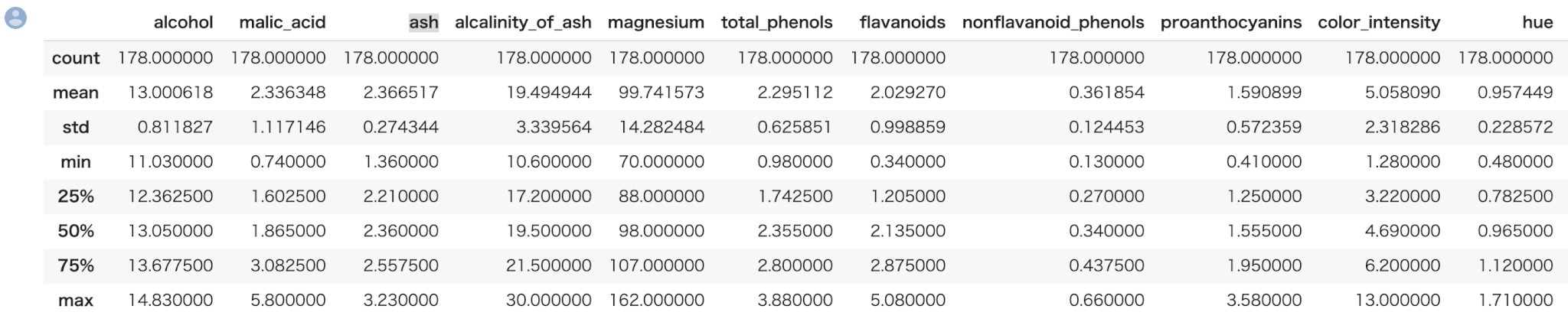
データセットの特徴量の型を確認します。pandasのinfoメソッドにより全てのカラムの型を確認できます。
In[]
1 | train.info() |
Out[]

全ての特徴量が浮動小数点数(float型)ということが確認できました。
Feature Scaling

Feature Scalingはデータを機械学習のアルゴリズムへ入力する前に特徴量に対して行う前処理のことです 。
すなわち、Feature Scalingとは特徴量間の値のスケールを整えることです。
次元削減や教師あり学習を行うにあたり、大事な前処理の1つとしてこの「Feature Scaling」があります。
例えば、上の train.describe() での結果において alcohol と malic_acid の結果を見てみましょう。
一方の平均は約13、もう一方は2.3と値のスケールが異なり、最小最大値もスケールが異なります。
このままkmeansなどの手法でクラスタリングを行うと、スケールの大きい特徴量(この場合だとalcohol)の影響力が強まってしまい、その特徴量だけで結果が決まってしまう傾向が強くなります。
※ 特徴量の単位をm→mmに変換しただけで結果が変わってしまったりします。
よって、よってFeature Scalingにより、スケールを特徴量間でなるべく統一します。
Feature Scalingの種類

Feature Scalingの種類として、大きく分けて『標準化』と『正規化』があります。
Feature Scalingの種類
- 標準化
- 正規化
- 標準化は平均が0、標準偏差が1になるようにデータをスケーリングします。
- 正規化は最小が0、最大が1になるようにデータをスケーリングします。
2つをどう使い分けるのかという点ですが、一つの観点として『外れ値らしきものがあるか無いか』という判断軸があります。
外れ値がなければ、正規化を使っても問題無い場合が多いです。
※ これは一概には言える事ではなく、細かく検定をする方法もありますが、非常に長くなってしまいますので、本記事ではその点については議論しません。
それでは特徴量ごとに『外れ値らしきものがあるか無いか』を、確認してみましょう。
seaborn の pairplot で全ての特徴量ごとのデータの分布を確認できます。
In[]
1 2 | import seaborn as sns sns.pairplot(train) |
Out[]
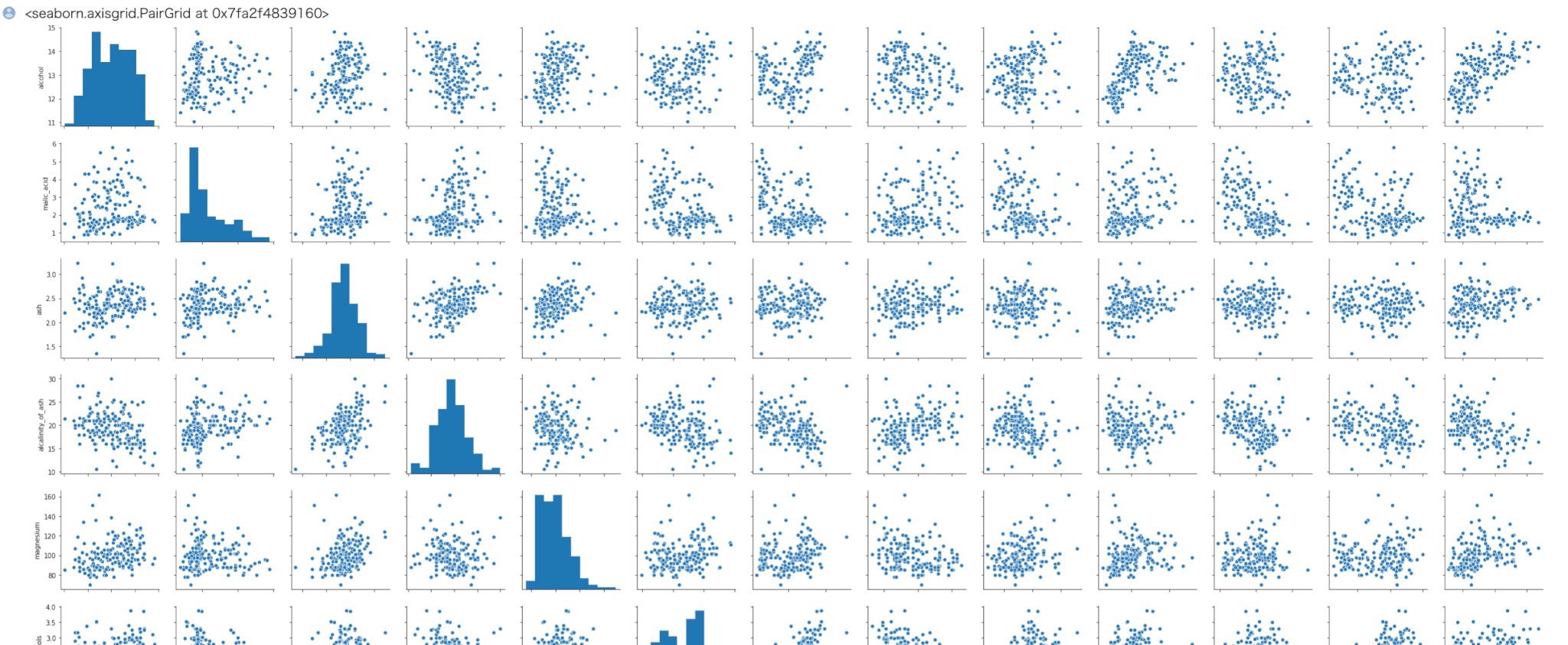
(注)一部のみを掲載しています。
以上より外れ値はなさそうなので、特徴量ごとに正規化の処理を行います。これはsklearnのMinMaxScaler関数を用います。
In[]
1 2 3 4 5 | from sklearn import preprocessing mms = preprocessing.MinMaxScaler() mms.fit(train) arr_mms = mms.transform(train) |
正規化が完了しました。もう一度特徴量ごとのデータの分布を確認してみましょう。
In[]
1 2 3 | train_mms = pd.DataFrame(arr_mms,columns=data_wine["feature_names"]) sns.pairplot(train_mms) |
Out[]
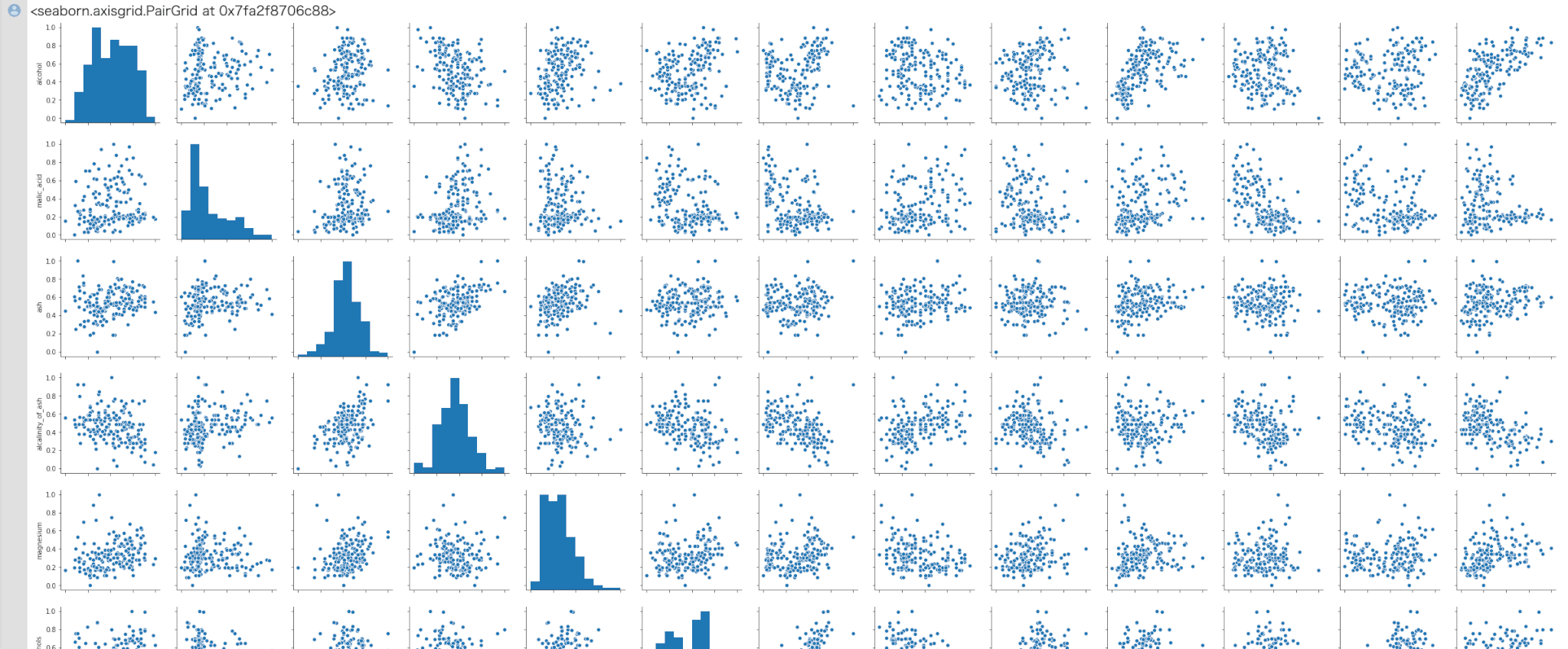
In[]
1 | train_mms.describe() |
Out[]

次元削減

続いて次元削減を行います。
次元削減とは今のデータセットには13個の多くの特徴量がありますが、それを13より少ない、例えば2つなどの特徴量で表せるように値を変換する処理を行います。
次元削減をするメリットは2つあります。
- データの可視化がしやすくなる
- よりクラスタリングがしやすくなる場合がある。
次元削減の手法は様々ありますが、ここでは次元削減としては基本的なPCAという手法を扱います。
これはsklearnの関数として用意されています。可視化しやすいよう、13→2次元に削減を行います。
In[]
1 2 3 4 5 | from sklearn.decomposition import PCA pca = PCA(n_components=2) pca.fit(train_mms) arr_2d = pca.transform(train_mms) train_2d = pd.DataFrame(arr_2d,columns=["pca_1","pca_2"]) |
次元削減が完了しました。 可視化してみましょう。
In[]
1 | sns.scatterplot( x='pca_1', y='pca_2', data=train_2d) |
Out[]
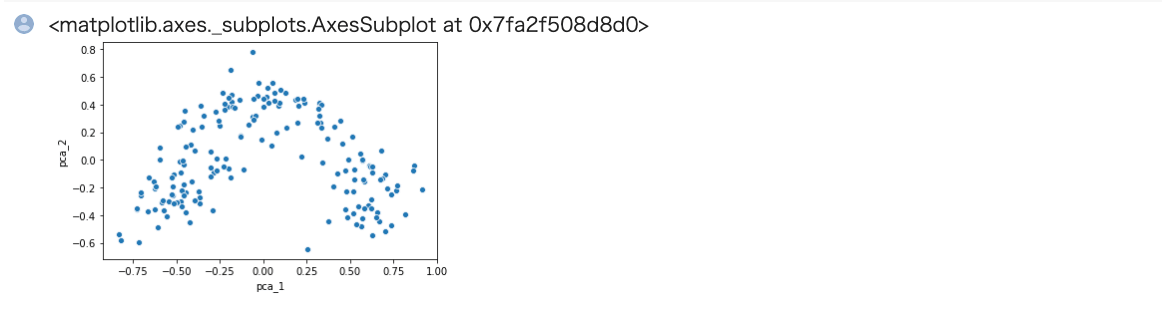
教師なし学習(クラスタリング)数の決定

続いて、本来は教師なし学習(クラスタリング)の処理に進みたいところですがここで1つ問題があります。
それはkmeansの場合はあらかじめクラスタリング数を決定しておく必要があることです。
データは無理やりでもよければいくらでも細かく分けれてしまいます。
『うまくデータを分けられている』とは、なるべく少ないクラスタ数でデータが集まっている集合(クラスタ)を1つ1つ分けられている状態を示します。
それを数値的に知る方法としてSSEというものがあります。SSEはクラスタの中心点とそのクラスタに属するデータ点の距離の和になります。
クラスタに属するデータ点がうまくまとまっている場合はSSEは小さくなり、まとまっていない場合はSSEは大きくなります。
SSEを使って『うまくデータを分けられる』クラスタリング数を見積もる方法をエルボー法といいます。わかりにくいと思いますので、実際に計算してみます。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 | import matplotlib.pyplot as plt list_sse = [] for i in range(1,11): km = KMeans(n_clusters=i, random_state=0) km.fit(train_2d) list_sse.append(km.inertia_) plt.plot(range(1,11),distortions,marker='o') plt.xlabel('Number of clusters') plt.ylabel('SSE') plt.show() |
Out[]
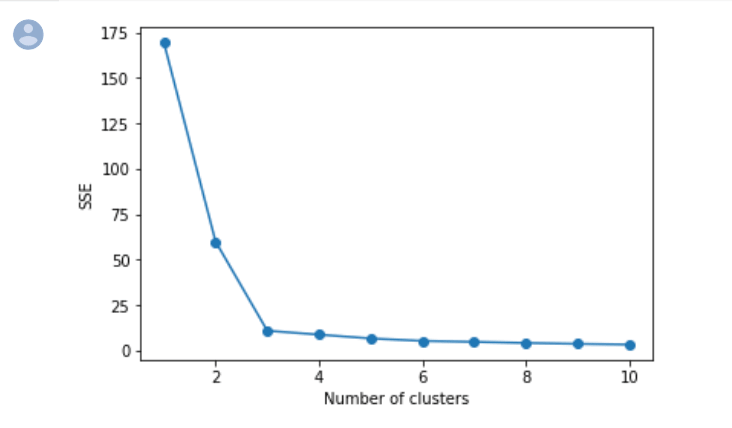
$X$ 軸がクラスタリング数、$Y$ 軸がSSEの値になっています。
SSEはクラスタ数が増えると減少しますが、その減少の割合は値によって異なるのがわかります。
特にクラスタ数が3以降はクラスタ数が増えてもあまりSSEは減少していません。
エルボー法ではこのような時に3を『うまくデータを分けられている』クラスタ数だと定性的に判断します。
教師なし学習(クラスタリング)

それではクラスタ数を3として再度kmeansでクラスタリングを行いましょう。
In[]
1 2 3 4 | from sklearn.cluster import KMeans kmeans = KMeans(n_clusters=3,random_state=0) kmeans.fit(train_2d) pred = kmeans.predict(train_2d) |
In[]
1 2 | train_2d["label"] = pred train_2d["label"] = train_2d["label"].astype("int") |
それではクラスタリングされたデータ点を可視化してみましょう。
In[]
1 | sns.scatterplot( x='pca_1', y='pca_2', hue="label",data=train_2d,palette="Set1") |
Out[]

定性的ですが、うまく分けられているのがお分かり頂けるかと思います。
そもそもこのデータセットの正解ラベルは3種類ありました。それとこの分類の方法が同じかはわかりませんが、このデータは3種類に分けることが妥当である可能性が高そうです。
クラスタリング結果の解釈

クラスタリングは終えましたが、教師なし学習によるクラスタリングはそれらのクラスタがどのような理由で分類されたかはわかりません。
それは1つの特徴量のみで分類している訳ではなく多くの特徴量から分類を行っているからです。
ただし、それを理由に分類の解釈を放棄してしまうと実際は困ることがあります。
クラスタごとのざっくりした特徴でも良いので捉えたいところです。
その場合はクラスタに分けた上で再度元の特徴量との関係性を眺めてクラスタの特徴を捉え直すことが有効となります。
それではクラスタごとの特徴量の分布を確認してみましょう。
In[]
1 | train["label"]=pred |
In[]
1 2 | import seaborn as sns sns.pairplot(train,hue="label",palette="Set1") |
Out[]
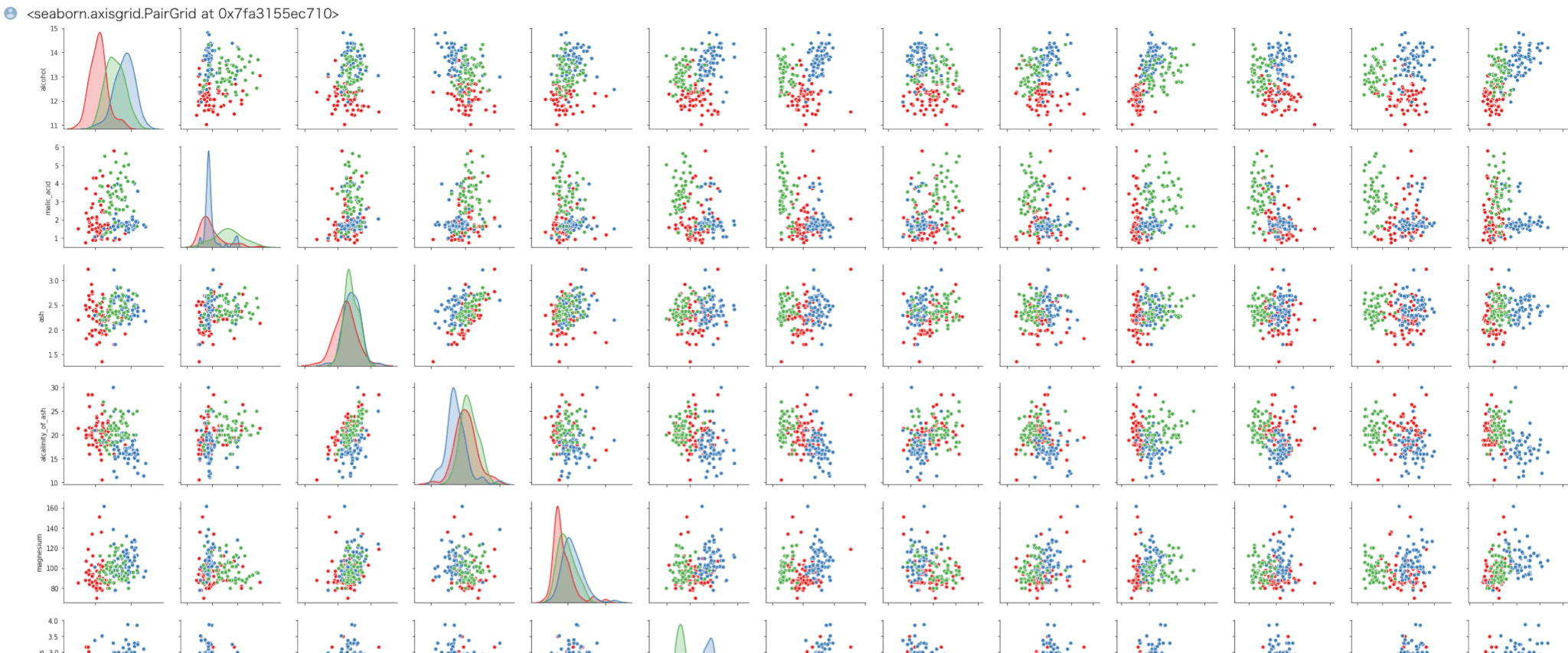
例えば、alcoholに着目してみるとクラスタごとに値が大中小に別れているのがわかります。
他の特徴をとりあえず考慮しなければ、アルコール濃度で分けられていると捉えることができます。
まとめ|【教師なし学習】機械学習でワインの品質判定を行ってみよう

以上がワインのデータセットを用いた教師あり学習の機械学習の練習問題となります。
実際に手を動かされると分かるかと思いますが、それほど難しい内容ではありません。
機械学習を勉強し始めた方の学習の一助になれば幸いです。
今回は以上となります。
