こんにちは。
医師やその他医療関係者の方でこれから人工知能を学習しようという先生は多いと思います。
もちろん、他職種の方でもこれから人工知能を学習しようという方も多いと思いますが、人工知能を学習する中で挫折する壁の一つが数学のうちの「微分」です。
本記事の内容
- 人工知能における必要な微分の知識
- 人工知能に微分はどの様に役立つのか。
- 人工知能において微分は何が求まるのか。
- 人工知能において微分は何に使えるのか。
以上について人工知能における微分の役割について解説していきます。
もし「人工知能やプログラミング」について再度学習し直したい方は、この記事を読む前に、こちらの記事を併せて読んで頂ければ理解が深まるかと思います。
-

【初心者向け】人工知能、機械学習、ディープラーニングの違いとは
続きを見る
では早速見ていきましょう。
人工知能に必要な微分の知識

人工知能に微分はどの様に役立つのか
中学高校時代には微積分を勉強していたと思いますが、人工知能の学習において微積分は非常に重要な役割を果たします。
今回のテーマのうち、
- 微分では何が求まるのか。
- 微分は何に使えるのか。
この2点について詳しく見ていきましょう。
人工知能において微分は何が求まるのか。
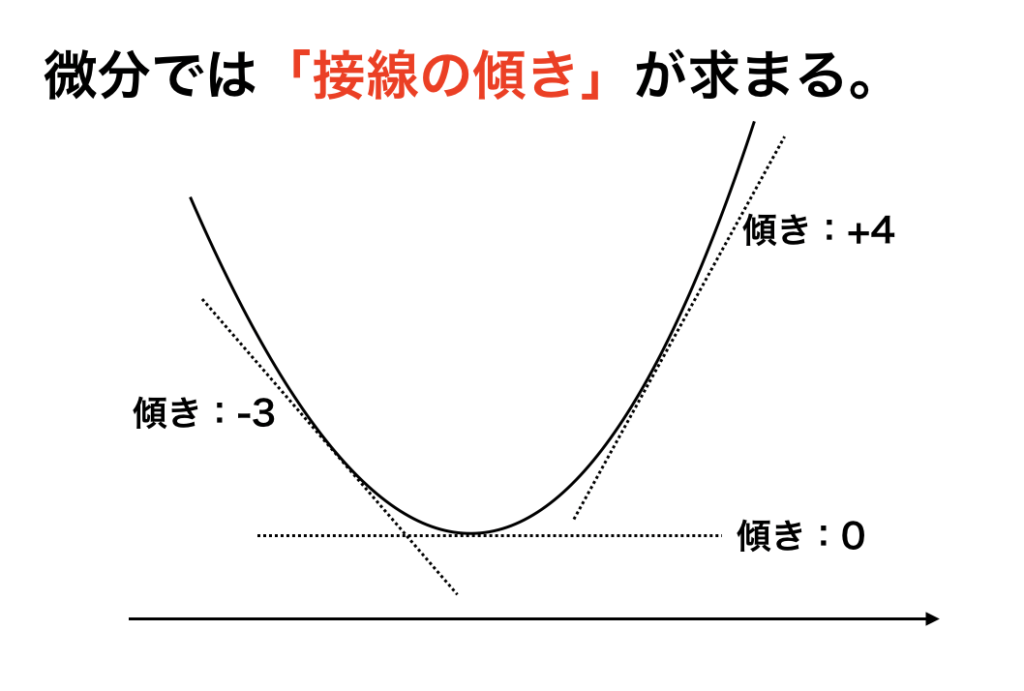
一言で言うと、微分を利用する事で「接線の傾き」が求まります。
例えば、上の図の様に曲線の接線の傾きが求まります。
では、この曲線の傾きである、傾き+2 や、傾き -3 は何に使えるのでしょうか。
特に傾き0は何を意味するのでしょうか。
人工知能において微分は何に使えるのか。
例えば、人工知能を用いた「家賃予測ツール」があるとします。
後に説明する「単回帰分析」では、「実際の家賃」と「予測する家賃の引き算」の値が最も小さい値を知りたいわけです。
この様な「実際の値」と「予測値」の差のことを「誤差」と言います。
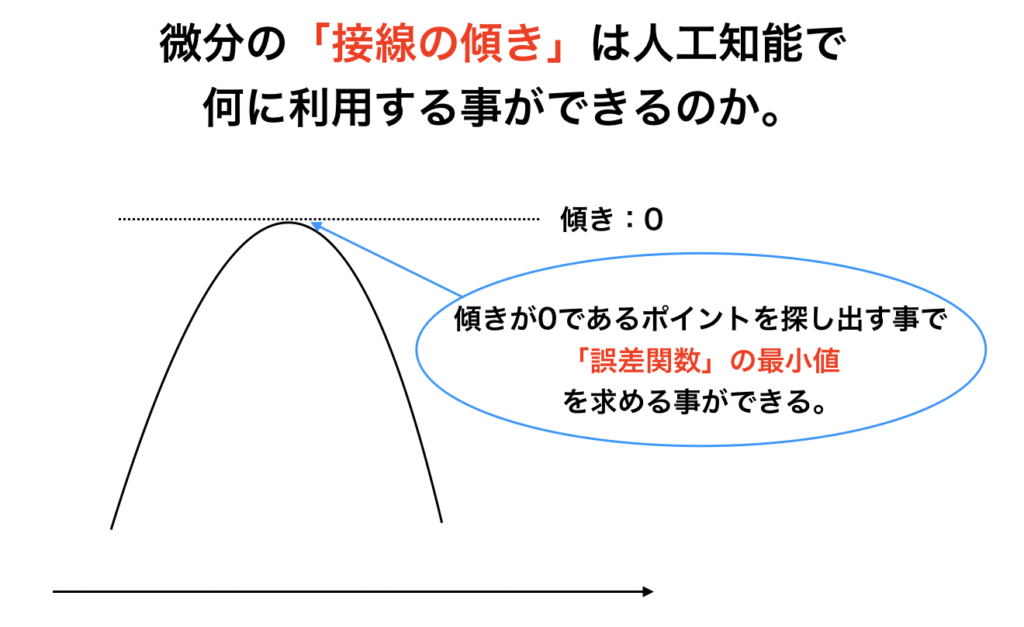
誤差を曲線化した時に傾きがマイナスになっている箇所が、誤差がもっとも小さな箇所となります。
すなわち、「誤差の傾き」が 0 である箇所を見つけることで(誤差関数の傾きが最小値の点を求める事で)「実際の値」と「予測値」の差が最も小さい点を知る事できる、と言うわけです。
- 良い予測をしたい -
これが機械学習の最終ゴールです。
良い予測をするためには「誤差」を可及的に小さくする必要があります。誤差関数の傾きが 0 の箇所を求めるのが、機械学習において微分が役に立つところとなります。
人工知能において必要な微分の知識|偏微分
偏微分とは「多変数の微分」である
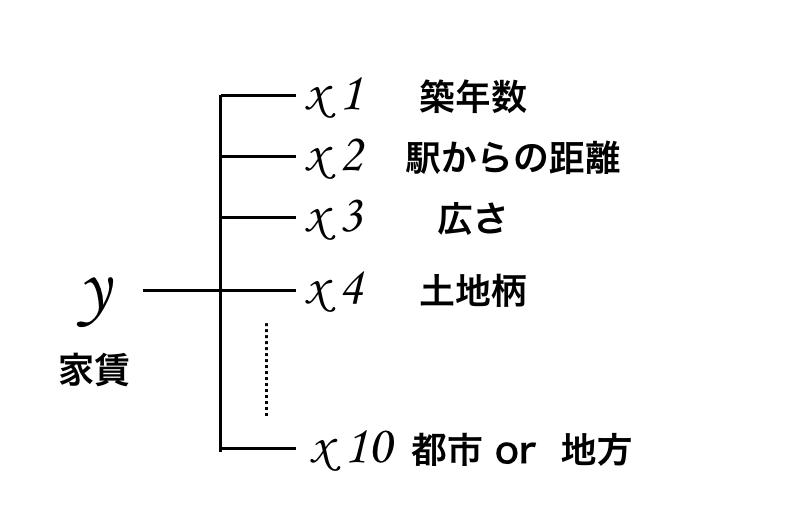
偏微分とは「多変数の微分」のことです。
- 家賃を $y$
- 家賃に影響を及ぼすファクターを $x$
とします。
家賃に影響を及ぼすファクターとしては「築年数」だけではなく、「駅からの距離」や「部屋の広さ」その他にも色々なものがあります。
そのため、上図の様に $x$ すなわち変数は数多く存在し、そのことを「多変数」と言います。
偏微分で使用する文字 - ∂|(ラウンド)ディー
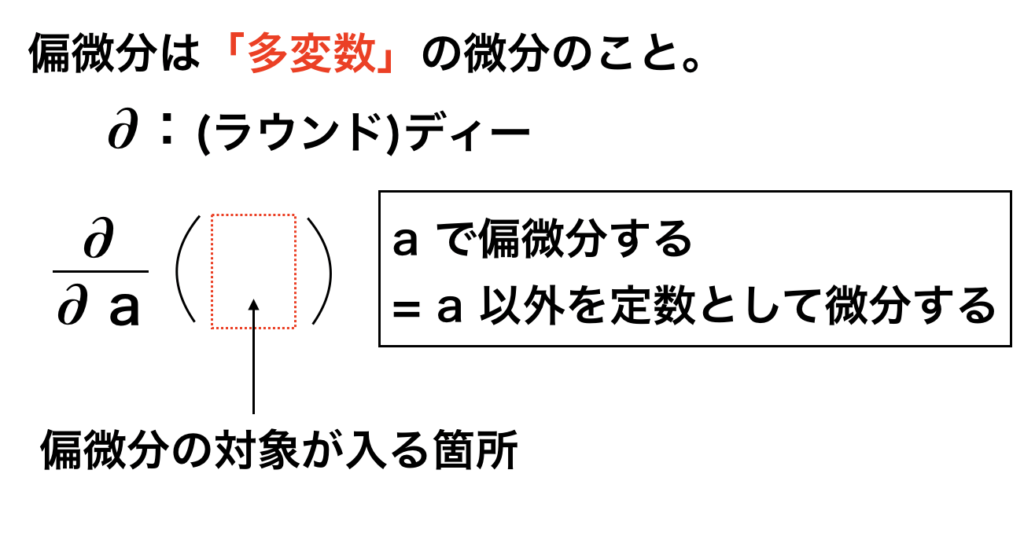
ここで、∂(ラウンドディー)という新しい文字が出てきます。
∂はラウンドディーまたは略してディーと言われます。
上図の式の∂(a)は a で微分する= a 以外を定数として微分する、という意味があります。
偏微分については、微分に関する基礎的な知識があれば大して難しくないので、それほど硬くならなくても大丈夫です。
微分を基本から学習するために

この様に微分は非常に重要な項目となります。
そのため、人工知能を学習するためには微分の基本を押さえておく必要があります。
わかりやすい参考書は書店でも沢山ありますが、基本をおさえるためにはどれでも大丈夫です。ある程度微分の概要をつかむことができれば良いでしょう。
学習において非常に重要なことは、微分のうち極限(lim)を中心に学習するのが良いでしょう。
まとめ

以上が人工知能と微分の基本的な関係になります。
偏微分についても出てきましたが、初めて知った!という方でも中学高校の微分、導関数の勉強をしっかりしていれば、それほど硬くなる必要はありませんのでご安心ください。
みなさんのお役に立てれば幸いです。
引き続き学んで頂きたい内容としては「単回帰分析(最小2乗法)」に関する記事があります。
ここまで理解ができた方は是非読み進んでみてください。
-

【Python】単回帰分析と最小2乗法の求め方【機械学習入門】
続きを見る
