こんにちは。産婦人科医のとみー(Twitter:@obgyntommy)といいます。
私は普段は画像系の機械学習の研究をしています。
研究の過程で Semantic segmentation を学習し、"U-net"についてまとめました。
U-netはFCN(fully convolution network)の1つであり、画像のセグメンテーション(物体がどこにあるか)を推定するためのネットワークです。
この記事の対象者は機械学習の初学者〜中級者の方です。
そのため、前線で活躍されている方には有益ではありません。
この記事では、まずはGANについて簡単に把握して頂き、次に実際にどの様な例で使用するのかということをGoogle Colaboratoryで手を動かして頂ければ幸いです。
Google Colaboratoryの使い方は以下の記事でまとめています。
-

Google Colaboratoryの使い方【完全マニュアル】
続きを見る
また、実際にU-netを使用した教師なし機械学習をGoogle Colaboratoryで行った試行例は以下になります。実際にPythonのコードを動かして頂く事も可能です。
-
Google Colab
続きを見る
誤りがあった場合にはお問い合わせフォームにまでご連絡いただけましたら幸いです。
こちらのスライドに沿って解説させて頂きます。
U-Netを用いた細胞画像のセグメンテーションについて
この章から、U-Netを用いて、実際の細胞画像対してセグメンテーションを行う流れを解説させて頂きます。
この記事で扱うデータセットは多数の細胞核の画像です。
これらの画像は撮影時のさまざまな条件下でデータが取得されています。
そのため、データを確認すると、細胞の種類、倍率、およびイメージングモダリティが異なっている事が分かります。
医療現場では、さまざまなモダリティ機器が使用されています。たとえば、強い磁場と電波によって体の断層を撮影するMRI(磁気共鳴診断装置)は、代表的なモダリティです。これは、現場ではMRと呼ばれています。また、X線によって体の断層を撮影するCT(コンピュータ断層撮影装置)も、モダリティのひとつに含まれるものです。モダリティにはその他にも、同じくX線を使用して臓器や血管などを画像化するCR(コンピュータ・ラジオグラフィ)やDR(デジタルX線撮影装置)、XA(血管造影X線診断装置)、US(超音波診断装置)、ES(内視鏡装置)などがあります。
よって、これらの多種多様な画像を汎用的にセグメンテーションするというのはとても難度の高いタスクです。
この記事ではその難度の高いタスクに対するU-Netモデルの有効性を確認することをゴールとて設定し、U-Netを学習する方の一助になればと思っています。
実装の流れとしては、ネット上でも良く取り扱われている他のチュートリアルとほぼ同様に、以下の流れで進めます。
実装の流れ
- データの確認、探索
- データの前処理
- U-Netのモデルの定義、トレーニング
- U-Netモデルの性能評価の確認
また、画像のアップロードや画像の処理やモデルのトレーニングを行う際に長い時間を要しますので、十分な時間を確保した上で以下を実行お願いします。(実際に、以下のコード実行は2時間ほどかかりました。)
また、モデルのトレーニングを行う場合はGPUの使用をお勧めします。
Google Colabを使う場合は上部『ランタイム』タブから『ランタイムのタイプを変更』を選択し、ハードウェアアクセラレータをGPUに変更をお願いします。
① データの確認、探索
今回用いるデータセットは kaggle のコンペティションで用いられたデータセットを用います。 (https://www.kaggle.com/c/data-science-bowl-2018/data)
もし本記事に記載されているコードを実行する場合は、上のサイトから一度お使いのパソコンにデータセットをダウンロードし、そのデータセットをこのcolabノートブック上にアップロードする必要があります。
方法については次のスライドを参考にして下さい。
トレーニングデータのzipファイルであるstage1_train.zipをアップロードしてから以下を実行してください。(アップロードは10分ぐらい時間がかかりました。)
まず、zipファイルの解凍を行います。
In[]
1 | ! unzip stage1_train.zip -d stage1_train |
Out[]

※ 出力内容の文字が潰れていてほぼ確認できないかもしれません。Google Colaboの方をご確認下さい。
次に、必要なライブラリをインポートしておきます。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | import os import time import copy from collections import defaultdict import torch import shutil import pandas as pd from skimage import io, transform import numpy as np from PIL import Image import matplotlib.pyplot as plt from torch.utils.data import Dataset, DataLoader, random_split from torchvision import transforms, utils from torch import nn import albumentations as A from albumentations.pytorch import ToTensor from tqdm import tqdm as tqdm from albumentations import (HorizontalFlip, ShiftScaleRotate, Normalize, Resize, Compose, GaussNoise) import cv2 from torch.autograd import Variable from torch.nn import Linear, ReLU, CrossEntropyLoss, Sequential, Conv2d, MaxPool2d, Module, Softmax, BatchNorm2d, Dropout from torch.optim import Adam, SGD import torch.nn.functional as F from PIL import Image from torch import nn import zipfile import random device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu') TRAIN_PATH = 'stage1_train/' |
続いてデータセットの読み込みを行います。
ここでは前処理の一部である画像のリサイズと、画像データ拡張も同時に行います。
画像のリサイズは様々なサイズの画像を全て固定のサイズに調整することにより1つのモデルによる対応が可能になります。
ここでは全ての画像を 256×256 の画像にリサイズしています。
また画像データ拡張は最近の画像系のディープラーニングの前処理とは一般的な処理で、画像に処理を加えることによりモデルの汎用化(予測精度を高める)ことが可能になります。
ここでは画像の正規化と水平垂直方向に画像をフリップさせる処理を追加しています。
「mask」はマスキング、つまり細胞のセグメンテーションがなされているデータであり、これが教師データとなります。
マスクに関しては今回は1つの細胞ごとに1つのファイルとなっているので、複数の画像を1つにまとめています。
トレーニングデータは一般的に入力画像と教師データ(mask)をペアとしてまとめ、このペアにより学習を行います。pytorchではこれらをDatasetクラスを用いてまとめます。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 | #画像データ拡張の関数 def get_train_transform(): return A.Compose( [ #リサイズ(こちらはすでに適用済みなのでなくても良いです) A.Resize(256, 256), #正規化(こちらの細かい値はalbumentations.augmentations.transforms.Normalizeのデフォルトの値を適用) A.Normalize(mean=(0.485, 0.456, 0.406), std=(0.229, 0.224, 0.225)), #水平フリップ(pはフリップする確率) A.HorizontalFlip(p=0.25), #垂直フリップ A.VerticalFlip(p=0.25), ToTensor() ]) #Datasetクラスの定義 class LoadDataSet(Dataset): def __init__(self,path, transform=None): self.path = path self.folders = os.listdir(path) self.transforms = get_train_transform() def __len__(self): return len(self.folders) def __getitem__(self,idx): image_folder = os.path.join(self.path,self.folders[idx],'images/') mask_folder = os.path.join(self.path,self.folders[idx],'masks/') image_path = os.path.join(image_folder,os.listdir(image_folder)[0]) #画像データの取得 img = io.imread(image_path)[:,:,:3].astype('float32') img = transform.resize(img,(256,256)) mask = self.get_mask(mask_folder, 256, 256 ).astype('float32') augmented = self.transforms(image=img, mask=mask) img = augmented['image'] mask = augmented['mask'] mask = mask[0].permute(2, 0, 1) return (img,mask) #マスクデータの取得 def get_mask(self,mask_folder,IMG_HEIGHT, IMG_WIDTH): mask = np.zeros((IMG_HEIGHT, IMG_WIDTH, 1), dtype=np.bool) for mask_ in os.listdir(mask_folder): mask_ = io.imread(os.path.join(mask_folder,mask_)) mask_ = transform.resize(mask_, (IMG_HEIGHT, IMG_WIDTH)) mask_ = np.expand_dims(mask_,axis=-1) mask = np.maximum(mask, mask_) return mask |
In[]
1 | train_dataset = LoadDataSet(TRAIN_PATH, transform=get_train_transform()) |
一枚の画像データとマスクの次元を確認します。
In[]
1 2 3 | image, mask = train_dataset.__getitem__(0) print(image.shape) print(mask.shape) |
Out[]
1 2 | torch.Size([3, 256, 256]) torch.Size([1, 256, 256]) |
画像枚数を確認します。
In[]
1 2 | #Print total number of unique images. train_dataset.__len__() |
Out[]
1 | 670 |
次に、入力画像とマスクのデータがどうなっているのか確認してみます。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | def format_image(img): img = np.array(np.transpose(img, (1,2,0))) #下は画像拡張での正規化を元に戻しています mean=np.array((0.485, 0.456, 0.406)) std=np.array((0.229, 0.224, 0.225)) img = std * img + mean img = img*255 img = img.astype(np.uint8) return img def format_mask(mask): mask = np.squeeze(np.transpose(mask, (1,2,0))) return mask def visualize_dataset(n_images, predict=None): images = random.sample(range(0, 670), n_images) figure, ax = plt.subplots(nrows=len(images), ncols=2, figsize=(5, 8)) print(images) for i in range(0, len(images)): img_no = images[i] image, mask = train_dataset.__getitem__(img_no) image = format_image(image) mask = format_mask(mask) ax[i, 0].imshow(image) ax[i, 1].imshow(mask, interpolation="nearest", cmap="gray") ax[i, 0].set_title("Input Image") ax[i, 1].set_title("Label Mask") ax[i, 0].set_axis_off() ax[i, 1].set_axis_off() plt.tight_layout() plt.show() visualize_dataset(3) |
Out[]
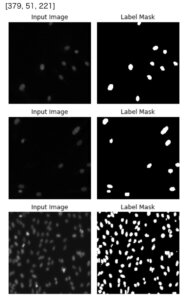
左列が入力画像、右列がマスクデータとなっています。
左列で細胞がある箇所に右列でマスクがなされていることが確認できます。
U-Netは左の画像を入力した際に右のようなマスクされた画像データが出力できれば良いということになります。
②データの前処理
続いて評価データ作成のため、トレーニングデータの一部を評価データとして分割します。
またpytorchではミニバッチ処理ができるようにDataLoaderクラスを作成します。
In[]
1 2 3 4 5 6 7 8 9 | split_ratio = 0.25 train_size=int(np.round(train_dataset.__len__()*(1 - split_ratio),0)) valid_size=int(np.round(train_dataset.__len__()*split_ratio,0)) train_data, valid_data = random_split(train_dataset, [train_size, valid_size]) train_loader = DataLoader(dataset=train_data, batch_size=10, shuffle=True) val_loader = DataLoader(dataset=valid_data, batch_size=10) print("Length of train data: {}".format(len(train_data))) print("Length of validation data: {}".format(len(valid_data))) |
Out[]
1 2 3 4 5 6 7 8 9 | split_ratio = 0.25 train_size=int(np.round(train_dataset.__len__()*(1 - split_ratio),0)) valid_size=int(np.round(train_dataset.__len__()*split_ratio,0)) train_data, valid_data = random_split(train_dataset, [train_size, valid_size]) train_loader = DataLoader(dataset=train_data, batch_size=10, shuffle=True) val_loader = DataLoader(dataset=valid_data, batch_size=10) print("Length of train data: {}".format(len(train_data))) print("Length of validation data: {}".format(len(valid_data)) |
③U-Netのモデルの定義、トレーニング
続いてU-Netのモデルを実装します。モデルについては解説記事か以下のサイトをご参照ください。
こちらのサイトを元に実装をしていきます。
個人的な印象として、U-Netモデルは細かい構成よりはモデルの全体構成から把握していった方が理解がしやすい印象です。
上記サイトのU-Netの解説記事にも記載している通り、以下の流れについてまず把握しましょう。
- FCNにあたる部分
- Up Samplingにあたる部分
- Skip Connectionにあたる部分
以上をまず把握します。
以下のコードコメント文にそれぞれがどこに該当するかを記載しています。
Skip Connection は torch.cat によりFCN時の出力と合わせています。
conv_bn_relu 関数は畳み込みとバッチ正規化と、活性化関数Reluをまとめています。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 | # UNet class UNet(nn.Module): def __init__(self, input_channels, output_channels): super().__init__() # 資料中の『FCN』に当たる部分 self.conv1 = conv_bn_relu(input_channels,64) self.conv2 = conv_bn_relu(64, 128) self.conv3 = conv_bn_relu(128, 256) self.conv4 = conv_bn_relu(256, 512) self.conv5 = conv_bn_relu(512, 1024) self.down_pooling = nn.MaxPool2d(2) # 資料中の『Up Sampling』に当たる部分 self.up_pool6 = up_pooling(1024, 512) self.conv6 = conv_bn_relu(1024, 512) self.up_pool7 = up_pooling(512, 256) self.conv7 = conv_bn_relu(512, 256) self.up_pool8 = up_pooling(256, 128) self.conv8 = conv_bn_relu(256, 128) self.up_pool9 = up_pooling(128, 64) self.conv9 = conv_bn_relu(128, 64) self.conv10 = nn.Conv2d(64, output_channels, 1) for m in self.modules(): if isinstance(m, nn.Conv2d): nn.init.kaiming_normal_(m.weight.data, a=0, mode='fan_out') if m.bias is not None: m.bias.data.zero_() def forward(self, x): # 正規化 x = x/255. # 資料中の『FCN』に当たる部分 x1 = self.conv1(x) p1 = self.down_pooling(x1) x2 = self.conv2(p1) p2 = self.down_pooling(x2) x3 = self.conv3(p2) p3 = self.down_pooling(x3) x4 = self.conv4(p3) p4 = self.down_pooling(x4) x5 = self.conv5(p4) # 資料中の『Up Sampling』に当たる部分, torch.catによりSkip Connectionをしている p6 = self.up_pool6(x5) x6 = torch.cat([p6, x4], dim=1) x6 = self.conv6(x6) p7 = self.up_pool7(x6) x7 = torch.cat([p7, x3], dim=1) x7 = self.conv7(x7) p8 = self.up_pool8(x7) x8 = torch.cat([p8, x2], dim=1) x8 = self.conv8(x8) p9 = self.up_pool9(x8) x9 = torch.cat([p9, x1], dim=1) x9 = self.conv9(x9) output = self.conv10(x9) output = torch.sigmoid(output) return output #畳み込みとバッチ正規化と活性化関数Reluをまとめている def conv_bn_relu(in_channels, out_channels, kernel_size=3, stride=1, padding=1): return nn.Sequential( nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size, stride=stride, padding=padding), nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True), nn.Conv2d(out_channels, out_channels, kernel_size=kernel_size, stride=stride, padding=padding), nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True), ) def down_pooling(): return nn.MaxPool2d(2) def up_pooling(in_channels, out_channels, kernel_size=2, stride=2): return nn.Sequential( #転置畳み込み nn.ConvTranspose2d(in_channels, out_channels, kernel_size=kernel_size, stride=stride), nn.BatchNorm2d(out_channels), nn.ReLU(inplace=True) ) |
損失関数について
セマンティックセグメンテーションの損失関数としてはBCELoss(Binary Cross Entropy)をベースとしたDiceBCELossがよく用いられます。
詳細な説明とコードは下記のサイトに記載があります。
» Kaggle Loss Function Library-Keras & Pytorch
考え方としては IoU に近く、予測した範囲が過不足なく教師データとなる領域を捉えているほど損失が低くなります。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | class DiceBCELoss(nn.Module): def __init__(self, weight=None, size_average=True): super(DiceBCELoss, self).__init__() def forward(self, inputs, targets, smooth=1): #comment out if your model contains a sigmoid or equivalent activation layer inputs = F.sigmoid(inputs) #flatten label and prediction tensors inputs = inputs.view(-1) targets = targets.view(-1) intersection = (inputs * targets).sum() dice_loss = 1 - (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth) BCE = F.binary_cross_entropy(inputs, targets, reduction='mean') Dice_BCE = BCE + dice_loss return Dice_BCE class DiceLoss(nn.Module): def __init__(self, weight=None, size_average=True): super(DiceLoss, self).__init__() def forward(self, inputs, targets, smooth=1): #comment out if your model contains a sigmoid or equivalent activation layer #inputs = F.sigmoid(inputs) #flatten label and prediction tensors inputs = inputs.view(-1) targets = targets.view(-1) intersection = (inputs * targets).sum() dice = (2.*intersection + smooth)/(inputs.sum() + targets.sum() + smooth) return 1 - dice |
セマンティックセグメンテーションの精度評価指標となるIoUのクラスを定義します。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | class IoU(nn.Module): def __init__(self, weight=None, size_average=True): super(IoU, self).__init__() def forward(self, inputs, targets, smooth=1): inputs = inputs.view(-1) targets = targets.view(-1) intersection = (inputs * targets).sum() total = (inputs + targets).sum() union = total - intersection IoU = (intersection + smooth)/(union + smooth) return IoU |
続いてU-Netの学習を行います。
まずモデル、オプティマイザ、損失関数のインスタンス作成を行います。
1epoch学習ごとに評価データによる精度評価を行い、精度評価の結果が最高のモデルを best_model_path 配下に保存する形になっています。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 | #<---------------各インスタンス作成----------------------> model = UNet(3,1).cuda() optimizer = torch.optim.Adam(model.parameters(),lr = 1e-3) criterion = DiceLoss() accuracy_metric = IoU() num_epochs=20 valid_loss_min = np.Inf checkpoint_path = 'model/chkpoint_' best_model_path = 'model/bestmodel.pt' total_train_loss = [] total_train_score = [] total_valid_loss = [] total_valid_score = [] losses_value = 0 for epoch in range(num_epochs): #<---------------トレーニング----------------------> train_loss = [] train_score = [] valid_loss = [] valid_score = [] pbar = tqdm(train_loader, desc = 'description') for x_train, y_train in pbar: x_train = torch.autograd.Variable(x_train).cuda() y_train = torch.autograd.Variable(y_train).cuda() optimizer.zero_grad() output = model(x_train) ## 損失計算 loss = criterion(output, y_train) losses_value = loss.item() ## 精度評価 score = accuracy_metric(output,y_train) loss.backward() optimizer.step() train_loss.append(losses_value) train_score.append(score.item()) pbar.set_description(f"Epoch: {epoch+1}, loss: {losses_value}, IoU: {score}") #<---------------評価----------------------> with torch.no_grad(): for image,mask in val_loader: image = torch.autograd.Variable(image).cuda() mask = torch.autograd.Variable(mask).cuda() output = model(image) ## 損失計算 loss = criterion(output, mask) losses_value = loss.item() ## 精度評価 score = accuracy_metric(output,mask) valid_loss.append(losses_value) valid_score.append(score.item()) total_train_loss.append(np.mean(train_loss)) total_train_score.append(np.mean(train_score)) total_valid_loss.append(np.mean(valid_loss)) total_valid_score.append(np.mean(valid_score)) print(f"Train Loss: {total_train_loss[-1]}, Train IOU: {total_train_score[-1]}") print(f"Valid Loss: {total_valid_loss[-1]}, Valid IOU: {total_valid_score[-1]}") checkpoint = { 'epoch': epoch + 1, 'valid_loss_min': total_valid_loss[-1], 'state_dict': model.state_dict(), 'optimizer': optimizer.state_dict(), } # checkpointの保存 save_ckp(checkpoint, False, checkpoint_path, best_model_path) # 評価データにおいて最高精度のモデルのcheckpointの保存 if total_valid_loss[-1] <= valid_loss_min: print('Validation loss decreased ({:.6f} --> {:.6f}). Saving model ...'.format(valid_loss_min,total_valid_loss[-1])) save_ckp(checkpoint, True, checkpoint_path, best_model_path) valid_loss_min = total_valid_loss[-1] print("") |
Out[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 | Epoch: 1, loss: 0.3565024137496948, IoU: 0.47438544034957886: 100%|██████████| 51/51 [04:47<00:00, 5.64s/it] Train Loss: 0.48769757210039627, Train IOU: 0.3539040680317318 Valid Loss: 0.40102399447385, Valid IOU: 0.43785814415006075 Validation loss decreased (inf --> 0.401024). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 2, loss: 0.379042387008667, IoU: 0.45029744505882263: 100%|██████████| 51/51 [04:46<00:00, 5.62s/it] Train Loss: 0.34592536383984135, Train IOU: 0.49084333578745526 Valid Loss: 0.23161793456358068, Valid IOU: 0.6330241718712974 Validation loss decreased (0.401024 --> 0.231618). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 3, loss: 0.2901915907859802, IoU: 0.5501654148101807: 100%|██████████| 51/51 [04:49<00:00, 5.67s/it] Train Loss: 0.20956240214553534, Train IOU: 0.6583620864971012 Valid Loss: 0.19625909538830028, Valid IOU: 0.6800956235212439 Validation loss decreased (0.231618 --> 0.196259). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 4, loss: 0.2104640007019043, IoU: 0.652265191078186: 100%|██████████| 51/51 [04:28<00:00, 5.26s/it] Train Loss: 0.17530548806283988, Train IOU: 0.7056634274183535 Valid Loss: 0.1730244755744934, Valid IOU: 0.714150640894385 Validation loss decreased (0.196259 --> 0.173024). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 5, loss: 0.2288087010383606, IoU: 0.6275975704193115: 100%|██████████| 51/51 [04:32<00:00, 5.35s/it] Train Loss: 0.17479715978398042, Train IOU: 0.7069565747298446 Valid Loss: 0.1570589542388916, Valid IOU: 0.7333086746580461 Validation loss decreased (0.173024 --> 0.157059). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 6, loss: 0.15453624725341797, IoU: 0.732300877571106: 100%|██████████| 51/51 [04:36<00:00, 5.42s/it] Train Loss: 0.14562876434887156, Train IOU: 0.75041708817669 Valid Loss: 0.1334028349203222, Valid IOU: 0.7659467879463645 Validation loss decreased (0.157059 --> 0.133403). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 7, loss: 0.15418952703475952, IoU: 0.7328328490257263: 100%|██████████| 51/51 [04:35<00:00, 5.41s/it] Train Loss: 0.12010368295744353, Train IOU: 0.7874887316834693 Valid Loss: 0.13047106827006621, Valid IOU: 0.771445656523985 Validation loss decreased (0.133403 --> 0.130471). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 8, loss: 0.9125477075576782, IoU: 0.045754872262477875: 100%|██████████| 51/51 [04:27<00:00, 5.25s/it] Train Loss: 0.14547663459590837, Train IOU: 0.7577330369283172 Valid Loss: 0.12613952861112707, Valid IOU: 0.7768697598401237 Validation loss decreased (0.130471 --> 0.126140). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 9, loss: 0.14393717050552368, IoU: 0.7483514547348022: 100%|██████████| 51/51 [04:24<00:00, 5.19s/it] Train Loss: 0.1282521825210721, Train IOU: 0.7753586395114076 Valid Loss: 0.1284707644406487, Valid IOU: 0.7739470530958736 description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 10, loss: 0.06418687105178833, IoU: 0.8793720602989197: 100%|██████████| 51/51 [04:23<00:00, 5.18s/it] Train Loss: 0.1223306281893861, Train IOU: 0.7844226874557196 Valid Loss: 0.13628508413539214, Valid IOU: 0.7611580035265755 description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 11, loss: 0.2969561815261841, IoU: 0.5420798659324646: 100%|██████████| 51/51 [04:23<00:00, 5.17s/it] Train Loss: 0.15399865426269232, Train IOU: 0.7393044098919513 Valid Loss: 0.1570578568121966, Valid IOU: 0.7328247445471147 description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 12, loss: 0.7912614345550537, IoU: 0.11656105518341064: 100%|██████████| 51/51 [04:22<00:00, 5.15s/it] Train Loss: 0.1293251911799113, Train IOU: 0.7799856288760316 Valid Loss: 0.11492833670447855, Valid IOU: 0.7946036948877222 Validation loss decreased (0.126140 --> 0.114928). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 13, loss: 0.2561001181602478, IoU: 0.5922384262084961: 100%|██████████| 51/51 [04:22<00:00, 5.15s/it] Train Loss: 0.11309224600885429, Train IOU: 0.7992275333872029 Valid Loss: 0.10989004373550415, Valid IOU: 0.8023735039374408 Validation loss decreased (0.114928 --> 0.109890). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 14, loss: 0.05128979682922363, IoU: 0.9024301767349243: 100%|██████████| 51/51 [04:23<00:00, 5.17s/it] Train Loss: 0.1112098822406694, Train IOU: 0.8008484361218471 Valid Loss: 0.10984138530843399, Valid IOU: 0.8024784081122455 Validation loss decreased (0.109890 --> 0.109841). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 15, loss: 0.06900733709335327, IoU: 0.8708987832069397: 100%|██████████| 51/51 [04:23<00:00, 5.16s/it] Train Loss: 0.1077261345059264, Train IOU: 0.8067927290411556 Valid Loss: 0.11400614065282486, Valid IOU: 0.7959509562043583 description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 16, loss: 0.16538548469543457, IoU: 0.7161799073219299: 100%|██████████| 51/51 [04:23<00:00, 5.17s/it] Train Loss: 0.10273515944387399, Train IOU: 0.815073522866941 Valid Loss: 0.10530715479570277, Valid IOU: 0.8099693726090824 Validation loss decreased (0.109841 --> 0.105307). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 17, loss: 0.150715172290802, IoU: 0.7380526065826416: 100%|██████████| 51/51 [04:24<00:00, 5.18s/it] Train Loss: 0.0996582589897455, Train IOU: 0.8197603436077342 Valid Loss: 0.10263854265213013, Valid IOU: 0.8142239276100608 Validation loss decreased (0.105307 --> 0.102639). Saving model ... description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 18, loss: 0.1428900957107544, IoU: 0.7499537467956543: 100%|██████████| 51/51 [04:25<00:00, 5.21s/it] Train Loss: 0.09917029796862135, Train IOU: 0.8204831375795252 Valid Loss: 0.10371375434538897, Valid IOU: 0.8125421825577231 description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 19, loss: 0.11792117357254028, IoU: 0.7890531420707703: 100%|██████████| 51/51 [04:25<00:00, 5.20s/it] Train Loss: 0.09963263717352175, Train IOU: 0.8197839400347542 Valid Loss: 0.10340490411309634, Valid IOU: 0.8131629999946145 description: 0%| | 0/51 [00:00<?, ?it/s] Epoch: 20, loss: 0.12009602785110474, IoU: 0.7855663895606995: 100%|██████████| 51/51 [04:24<00:00, 5.18s/it] |
④U-Netモデルの性能評価の確認
学習と評価が終了しましたので、エポックごとの損失、精度の変化をグラフ化します。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | import seaborn as sns plt.figure(1) plt.figure(figsize=(15,5)) sns.set_style(style="darkgrid") plt.subplot(1, 2, 1) sns.lineplot(x=range(1,num_epochs+1), y=total_train_loss, label="Train Loss") sns.lineplot(x=range(1,num_epochs+1), y=total_valid_loss, label="Valid Loss") plt.title("Loss") plt.xlabel("epochs") plt.ylabel("DiceLoss") plt.subplot(1, 2, 2) sns.lineplot(x=range(1,num_epochs+1), y=total_train_score, label="Train Score") sns.lineplot(x=range(1,num_epochs+1), y=total_valid_score, label="Valid Score") plt.title("Score (IoU)") plt.xlabel("epochs") plt.ylabel("IoU") plt.show() |
以上の通り、epoch数が進むにつれて損失が減り、精度が向上していることがわかります。
これは機械学習においてはモデルの学習が進み、より汎化性能(予測性能)が増して行っていることを意味しています。
次に、作成した学習したモデルを利用して、実際のモデルによるセマンティックセグメンテーションの結果を表示してみます。
まず作成したモデルを読み込みます。
In[]
1 | model, optimizer, start_epoch, valid_loss_min = load_ckp(best_model_path, model, optimizer) |
続いて入力画像と教師データ、モデルによる出力を表示する関数を用意し、出力を行います。
In[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | def visualize_predict(model, n_images): figure, ax = plt.subplots(nrows=n_images, ncols=3, figsize=(15, 18)) with torch.no_grad(): for data,mask in val_loader: data = torch.autograd.Variable(data, volatile=True).cuda() mask = torch.autograd.Variable(mask, volatile=True).cuda() o = model(data) break for img_no in range(0, n_images): tm=o[img_no][0].data.cpu().numpy() img = data[img_no].data.cpu() msk = mask[img_no].data.cpu() img = format_image(img) msk = format_mask(msk) ax[img_no, 0].imshow(img) ax[img_no, 1].imshow(msk, interpolation="nearest", cmap="gray") ax[img_no, 2].imshow(tm, interpolation="nearest", cmap="gray") ax[img_no, 0].set_title("Input Image") ax[img_no, 1].set_title("Label Mask") ax[img_no, 2].set_title("Predicted Mask") ax[img_no, 0].set_axis_off() ax[img_no, 1].set_axis_off() ax[img_no, 2].set_axis_off() plt.tight_layout() plt.show() visualize_predict(model, 6) |
Out[]
1 2 3 | /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:5: UserWarning: volatile was removed and now has no effect. Use `with torch.no_grad():` instead. """ /usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:6: UserWarning: volatile was removed and now has no effect. Use `with torch.no_grad():` instead. |

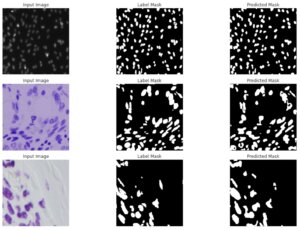
以上の結果を確認してみます。
Label Mask(教師データ)とPredicted Mask(モデル予測データ)を比較すると完全に等しくはなりませんが、モデルは比較的教師データに近いセグメンテーションをしていることがわかります。
U-Netはピクセルごとの画像の濃淡を元にセグメンテーションしているので、教師データより細かいセグメンテーションを行なっていることも分かるかと思います。
また、今回用いた学習データは数百枚のトレーニングデータしか用いておらず、(タスクにもよりますが)CNNなどで必要となるトレーニングデータの量と比べるととても少ないと感じられると思いますが、実際にデータ数が少ない時にも有用な方法です。(自分の研究ではそうでした。)
作成したモデルは保存していますので、このモデル再使用することでお手持ちの別の画像にもセグメンテーションをすることができますので、是非色々試して考察を行なって頂ければ幸いです。
今回は以上となります。
