検定（統計学的仮説検定）とは

こんにちは。産婦人科医のとみーです。（Twitter：@obgyntommy）

本記事では検定（統計学的仮説検定）について、解説していきます。

仮説検定あるいは統計的仮説検定（statistical hypothesis testing）とは、母集団分布の母数に関する仮説を標本から検証する統計学的方法のひとつ。のことを言います。

» Wikipedia【引用】

対象としては、統計検定2級の取得を目指している方、または資格取得に限らず統計の基本的な知識を学びたい方に向けた記事となります。

少し話はそれますが、「統計的仮説検定の方法論は、ネイマン=ピアソン流の頻度主義統計学に基づくものと、ベイズ主義統計学に基づくものとの二つに大きく分けられる」と言われていますが、これには議論があるところで、個人的には否定的な意見です。

それでは早速、見ていきましょう。

検定（統計学的仮説検定）とは

検定とは、得られたデータ（標本）を使って集団（母集団）について判断を下すことです。

例えば、ある新しい降圧薬の効果を調べたい場合なら、実際に薬を服用した人のデータを使って、その薬を多くの人が使った場合に効果があるかを判断するということになります。

ここで、具体的に考えてみます。

ある新しい降圧薬を10人が服用した結果、以下のように血圧が変化したとします。

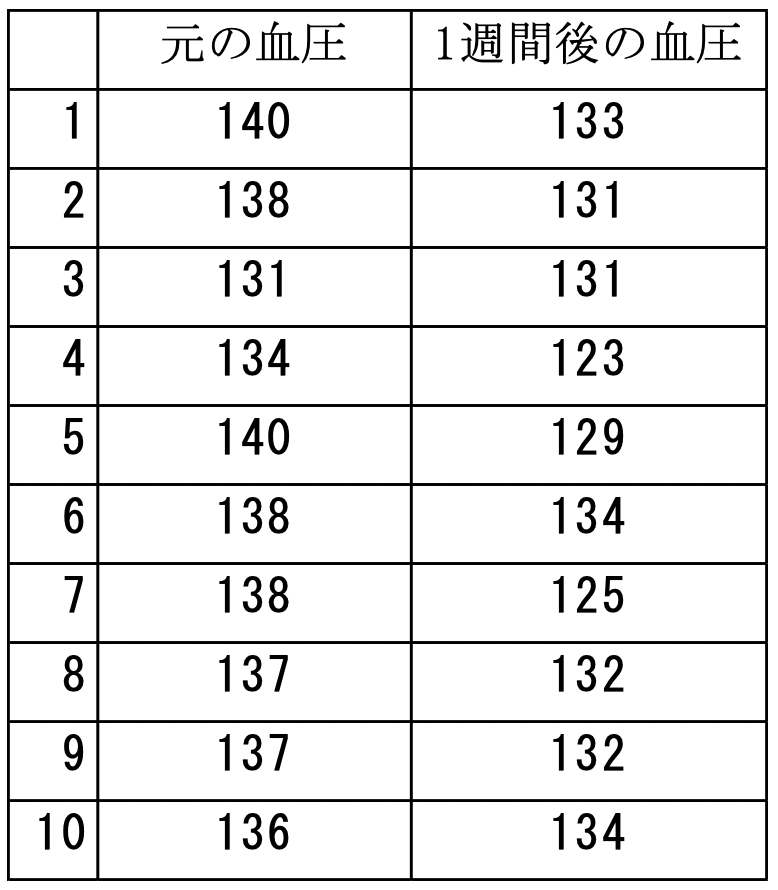
全体的に見ると、血圧は下がっているように見えます。

この新しい薬は降圧の効果があると結論付けることはできるでしょうか。

新しい薬のおかげで血圧が下がったという人もいると思いますが、このぐらいの変化は誤差だと言う人もいると思います。

ここで統計学に基づいて結論を出す方法が検定です。

具体的な検定方法の説明に入る前に、今回は検定とは何か、そのベースとなる考え方についてお話します。

帰無仮説と対立仮説【研究で立てるべき2つの仮説】

多くの研究は、「こういうことを証明したい」というモチベーションに基づいて行われます。

例えば、新しい降圧薬は血圧を下げる効果があるといった予想したり、たくさん笑うほど免疫細胞が活発になるに違いない（この辺りの知識は詳しくありません）と考える様なモチベーションです。

こういった予想や考えが、仮説です。

※ 医学の場合、記述的研究も多く行われるため、証明したいものがない場合もあります。

ここで、統計学の仮説は2種類あります。

ひとつが帰無仮説と呼ばれるもので、もうひとつが対立仮説と呼ばれるものです。

対立仮説とは一般用語としての仮説と同じ、証明したいものです。

先ほどの例でいえば、新しい降圧薬は血圧を下げる効果がある、といったものです。

統計用語では、対立仮説はH1と呼ばれます。

反対に、帰無仮説とは効果がないとする仮説です。

先ほどの例でいえば、新しい降圧薬は血圧を下げない、といったものです。

統計用語では、帰無仮説はH0と呼ばれます。

この数字の通り、検定では帰無仮説のほうを最初に立てます。

例えば、新しい降圧薬の効果を明らかにするのなら、まず帰無仮説「新しい降圧薬は血圧を下げない」を立てます。

それを「『血圧が偶然下がった』と言える確率は無視できるほど低い」という論理で仮説を否定する、すなわち二重否定することで対立仮説のほうが正しかったとするのです。

二重否定することで明らかにしたかった仮説を証明するというのは、統計学だけではなく科学全般に共通する考え方です。

それというのも仮説を検証するのは不可能に近いけれども、反証することはできるからです。

「反証とは」

その仮定的事実や証拠が真実でないことを立証すること。そのための証拠。

» Oxford Languagesの定義【引用】

この考えの例にあげられるのが、以下の「ヘンペルのカラス」です。

「全てのカラスは黒い」ことを証明するのは、不可能と言えます。

しかし、「全てのカラスは黒い」を反証するのは、簡単ですね。一匹でも白いカラスを見つければ良いので。

両側検定と片側検定

先ほどの降圧薬の例では、「薬は血圧を下げる」と一方向の効果しか持ちません。

こういった一方向の対立仮説を検定する場合を片側検定と言います。

一方、特定の食べ物だけを食べる「〇〇だけでダイエット」の場合だと、どうなるでしょうか。

ダイエットなので体重を下げると思いたいところですが、かえって体重が増えてしまうという話を聞くこともあります。

このような場合、「〇〇だけでダイエットをすることで体重に変化が見られる」という対立仮説が考えられます。

方向性がどちらでもよい場合の仮説を検定する場合は、両側検定を行います。

片側検定と両側検定の違いは、帰無仮説を棄却して対立仮説の採用を決定する基準の厳しさです。

まず片側検定の場合、計算した結果の数値が右のピンク枠で囲った部分にあれば、帰無仮説を棄却して対立仮説を採用することになります。

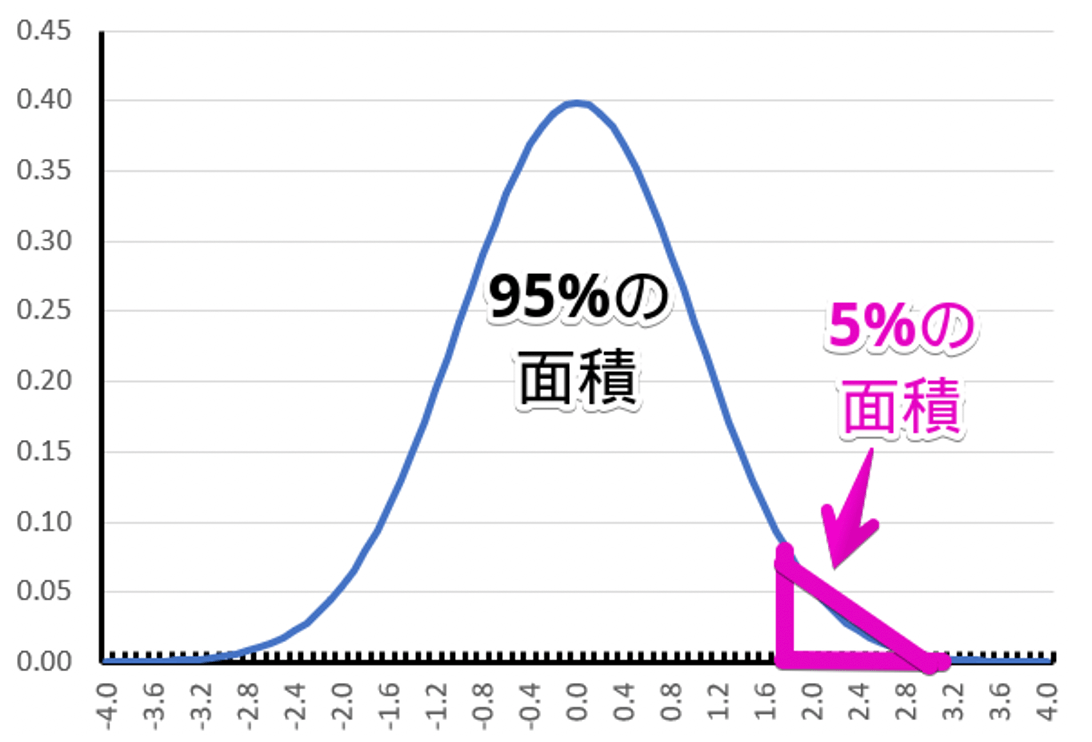
一方対立検定の場合、計算した結果の数値が右あるいは左のピンク枠で囲った部分にあれば、帰無仮説を棄却して対立仮説を採用することになります。

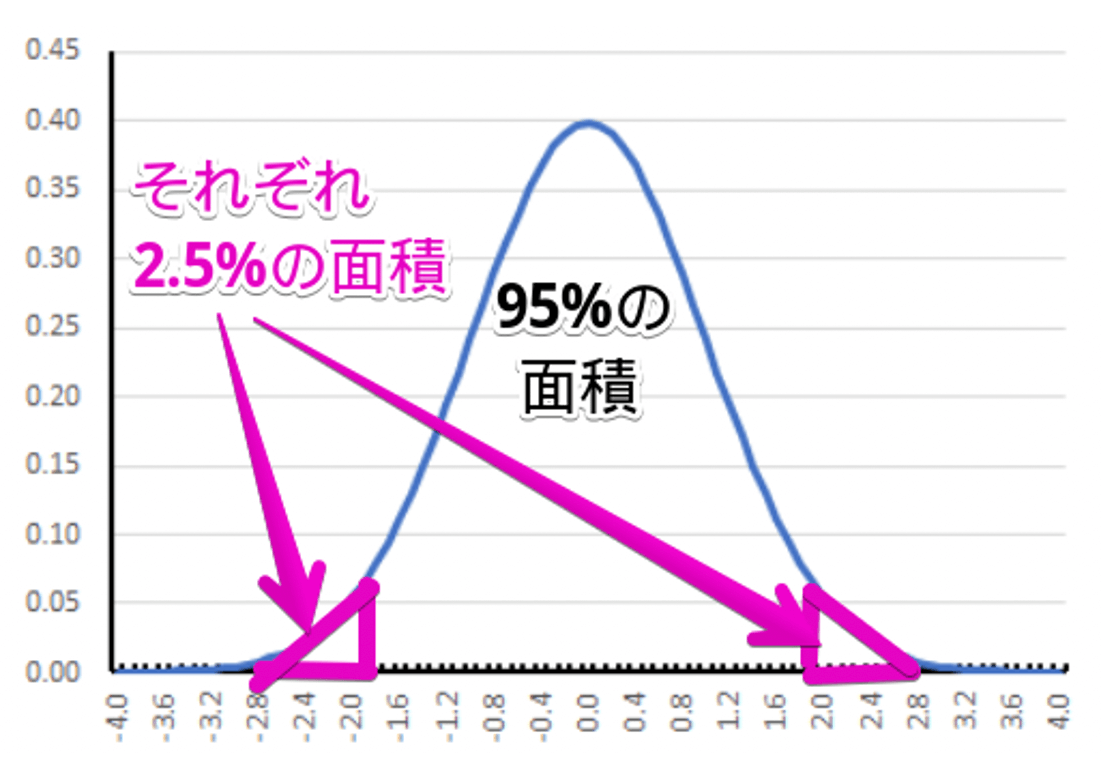
どちらも同じ5％分の面積のなかに数値が入ればよいのですが、片側検定のほうが $x$ 軸の値が若干小さいです。

このことは、片側検定のほうが帰無仮説を棄却して対立仮説を採用しやすいことを意味します。

とはいえ、自分が立てた対立仮説が証明されやすいから片側検定で検定しようというのは、恣意的な行為なので行うべきでありません。

証明したい仮説に合わせて片側検定か両側検定か選ぶことが、正しい仮説検定です。

仮説が証明されたという様々な判断基準について

ここまで帰無仮説を棄却して対立仮説を採用すると解説しましたが、これには数値的な判断基準があります。

$p$ 値とは【対立仮説を採用する基準】

「$p<0.05$」あるいは「$p <0.01$」という表記を見たことがある人もいるかもしれません。

$p$ 値とは、偶然の結果、独立変数による差が見られた（分析内容によっては変数同士の関連）確率のことです。

$p$ 値は有意水準や$1-α$などと呼ばれることもあります。

逆に、$α$ は危険率とも呼ばれ、第一種の過誤（本当は帰無仮説が正しいのに、誤って対立仮説を採用してしまうこと）を意味します。

降圧薬の例でいうならば、「降圧薬の服用前後で血圧は変わらない」という帰無仮説に対して、今回の血圧の差が偶然出るとしてその確率 $p$ はどのくらいかということになります。

「$p<0.05$」というのは、確率$p$の値が5%未満であることを意味します。

つまり、偶然による差（あるいは関連）が見られた確率が5%未満であるということです。

なお、仮に計算の結果  $p$  値が $5%$ 以上の数値になったとします。

この場合、帰無仮説が正しいのかというと、そうはなりません。

対立仮説と帰無仮説のどちらが正しいのか分からないという状態になります。

実際に研究を行うなかでこのような状態になったなら、研究方法を見直して再び実験・調査を行い、仮説検定をし直すということになります。

ちなみに、多くの研究で $p<0.05$ と書かれていると思いますが、これは慣例的に $5%$ が基準となっているためです。

「$p<0.05$」が$5％$未満の確率なら、「$p<0.01$」は1%未満の確率で起こることなので、独立変数の効果が強いと思われる方もいるかもしれません。

しかし、この考えは誤っています。

詳しくは、「違いが認められた」と「どのくらいの効果があるか」は別のもので、すなわち「効果量」で説明します。

検出力【帰無仮説を正しく棄却する確率】

検出力とは、帰無仮説が正しくないときに帰無仮説を正しく棄却する確率のことです。

検出力は $1-β$  で表されることもあります。

$β$ という文字が出てきましたが、ベータは第二種の過誤（本当は対立仮説が正しいのに、誤って帰無仮説を採用してしまう）をきたす確率を意味します。

そのため、検出力は第二種の過誤が前提の考えとなります。

有意水準と検出力は別々の概念ではなく、関連があります。

例えば、Aさんが日本人かアメリカ人かを身長から考えてみます。

まず、日本人とアメリカ人の身長の分布図は以下のようなイメージになります。

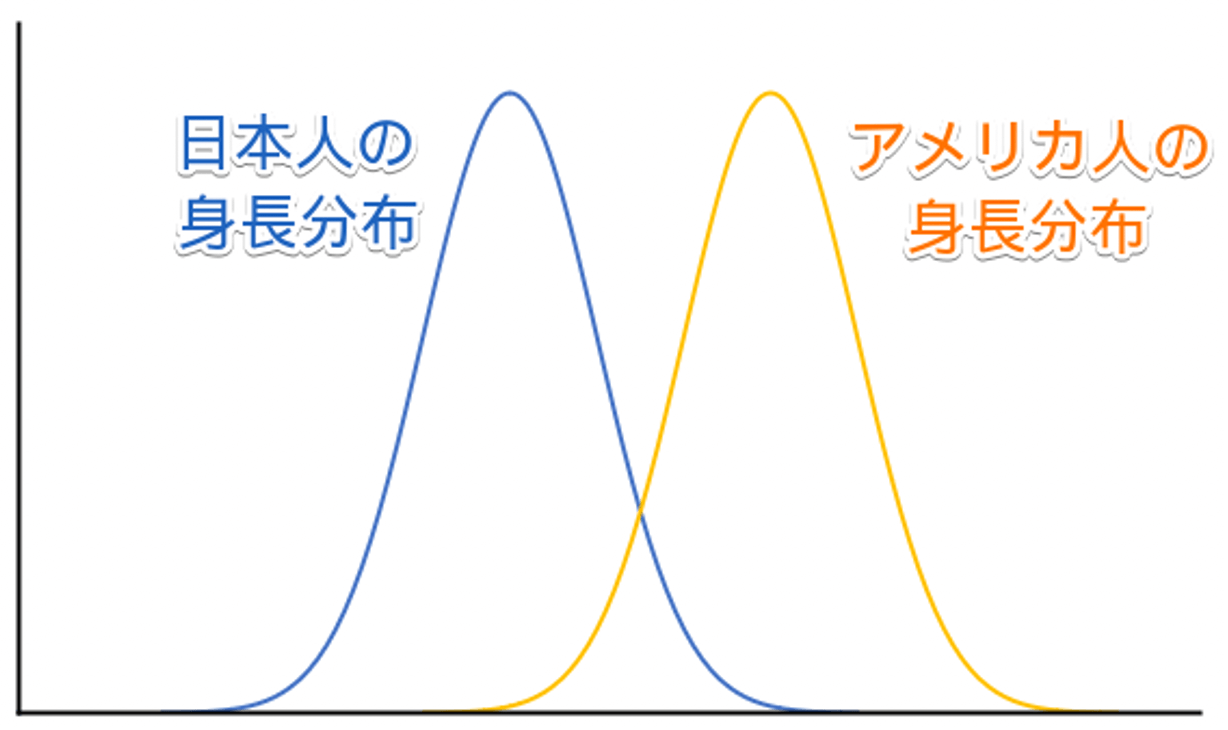
ここで、Aさんの身長はピンク丸の位置だとします。

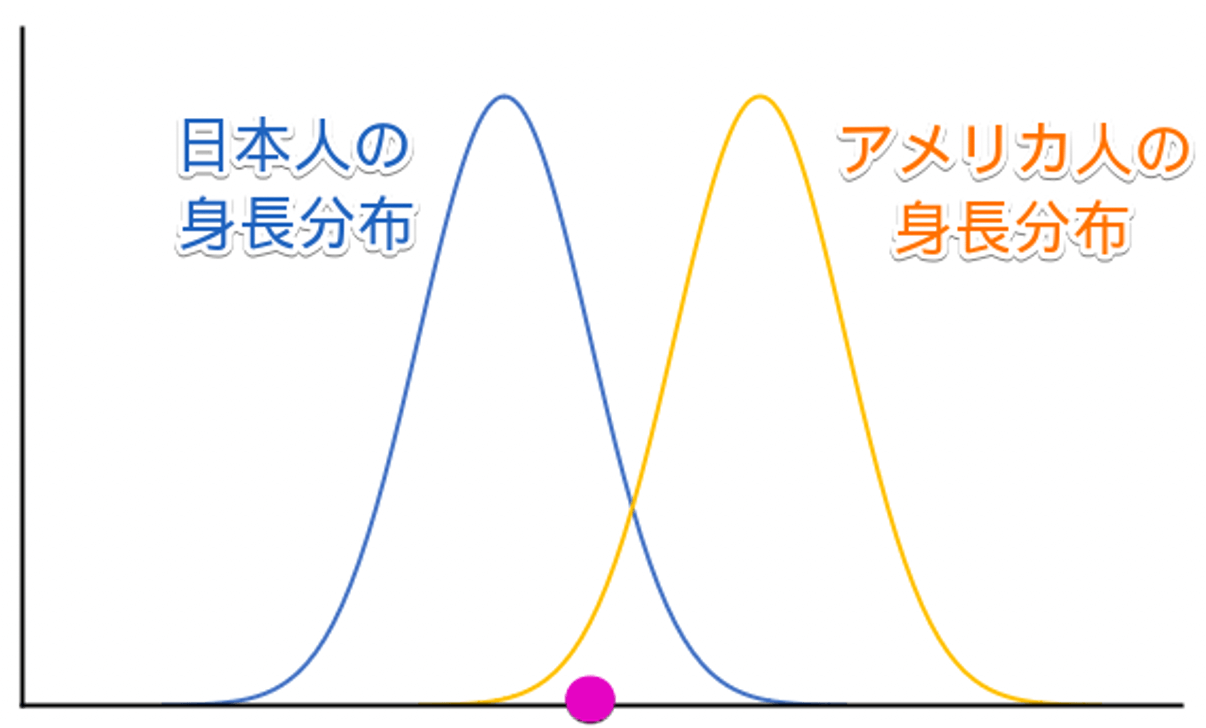
ピンク丸の位置の人は、日本人の中では平均身長よりも結構高いようですが、アメリカ人の中ではかなり低いようです。

とはいえ、Aさんは日本人であり、アメリカ人ではないと断言するのも早計です。

そこで、以下の仮説を立てます。

先ほどの図に有意水準や $α$、$β$、検出力を加えたものが以下の図です。

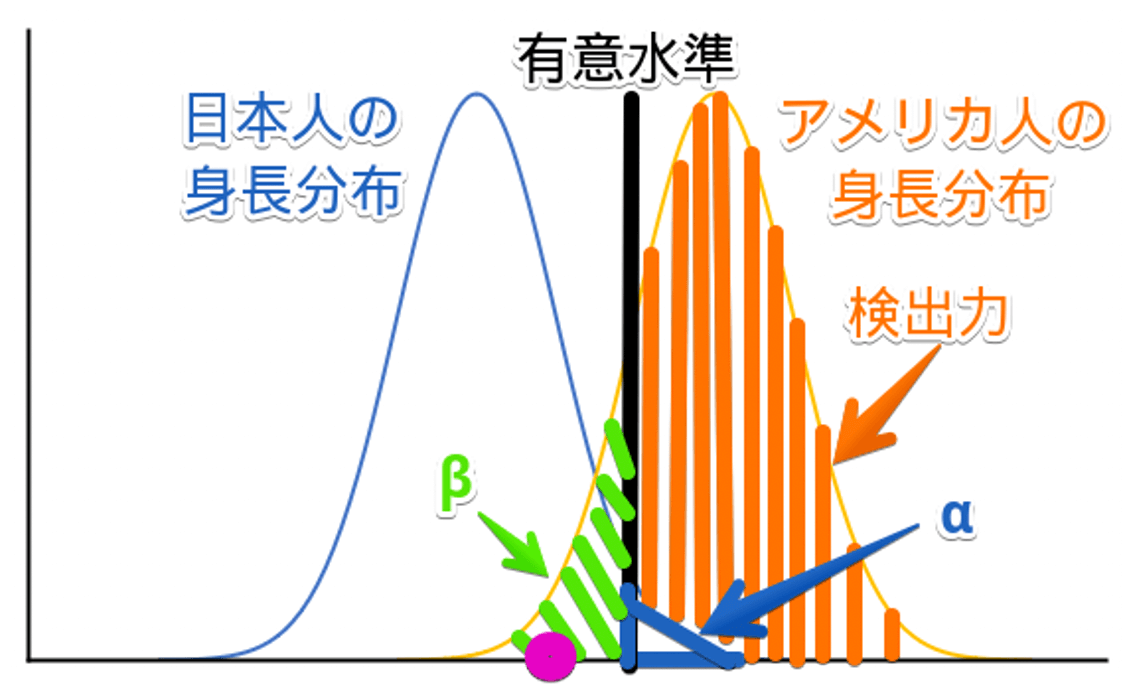
日本人の身長分布から見ると、有意水準よりも左側にピンク丸あります。

よって帰無仮説は棄却されるので、Aさんは日本人と予測できます。

また、ここでの $α$ や $β$ 、検出力について解説します。

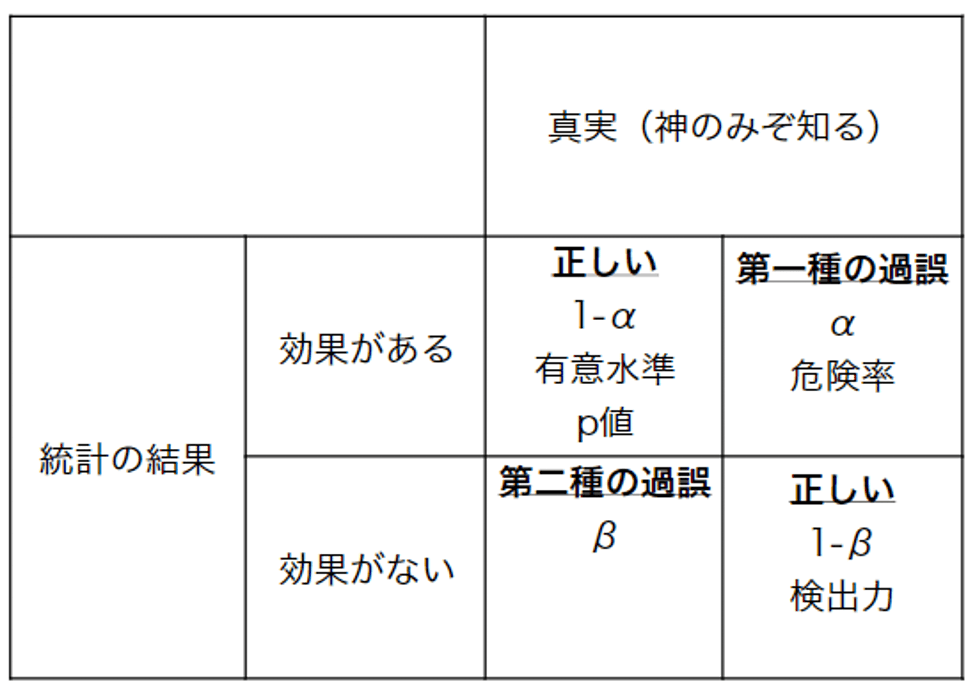
$p$ 値、検出力、第一種の過誤、第二種の過誤の関係

ここまで $p$ 値、検出力、第一種の過誤、第二種の過誤と色々な専門用語が出てきました。

表にまとめると、以下のようになります。

効果量とは【「違いが認められた」と「どのくらいの効果があるか」は異なる】

有意水準 $p$ 値は「確率論的に違いが認められたこと」を意味しますが、「どのくらい効果があるか」とは関連しません。

例えば同じ平均値であっても、10人ずつで比較場合よりも20人ずつで比較した場合のほうが  $p$ 値は小さくなります。

それというのも、「推測統計学とは」で解説したように、中心極限定理よりサンプルサイズが大きいほうが平均値のばらつきが少ないためです。

「どのくらいの効果があるか」はどうやって調べるかというと、効果量というもので調べることができます。

効果量は統計検定の種類によって指標や大きさの基準が異なります。

効果量の詳しい解説は、実際にそれぞれの統計検定の解説をするときに併せて説明する事にします。

パラメトリック検定とノンパラメトリック検定

統計検定には色々なものがありますが、次回以降の記事では以下の統計検定2級でも出題される以下の統計検定を解説していきます。

新しい降圧薬は本当に役に立つのか → t検定（2つの平均値の間に差があると統計的に認められるかを分析する）

ストレスが多いのが悪いのはみんな知っているけど、実はストレスがないのも悪い、ほどほどが一番 → 一要因の分散分析（3つ以上の平均値の間に差があると統計的に認められるかを分析する）

「ただしイケメンに限る」は本当なのか？  →  二要因の分散分析（相乗効果（1+1が2よりももっと大きなものとなる）が統計的に認められるかを分析する）

時代劇で見るサイコロ博打。このサイコロはイカサマサイコロじゃないかい？ → χ2検定（特定の項目だけが多くor少なくなっていないか統計的に分析する）

笑いは健康に良いって科学的に本当？ → 相関分析（あるデータの値が増えるほど別のデータの値も増える or あるデータの値が増えるほど別のデータの値が減るかを分析する）

「自称」専門家ほど実は知ったかぶりするので注意 → 回帰分析、重回帰分析（原因となるデータと結果となるデータを $y（結果）=  ax（原因）+b$の式で表せることができるかを調べる分析のこと。

重回帰分析になると原因となるデータの種類が増えて、$y（結果）=ax1（原因1）+b x2 （原因2）cx3（原因3）+d $となります。）

パラメトリック検定【精度は高いけど分析に条件のある】

先ほどあげた統計検定は、大きくは2種類に分けられます。

χ2 検定以外の統計検定は全てパラメトリック検定に分類されます。

パラメトリックとは「parametric母数に関すること」という意味です。

これは、パラメトリック検定では平均値や分散などを分析で使うためです。

そのため、パラメトリック検定を行う分析では平均値や分散が分布の特徴を示す正規分布となっているのが前提となります。

なお、データが少なすぎる場合もパラメトリック検定は行うことができません。

パラメトリック検定の分析で使う平均値や分散は外れ値のような極端な数値の影響を受けやすいためです。

しかし、このような制限はあるものの、一般的に数値データの間隔尺度・比率尺度を扱う研究ではノンパラメトリック検定よりもパラメトリック検定のほうがよく行われます。

理由としては、パラメトリック検定は分析精度が高いためです。

そのため、一般的に統計検定ではパラメトリック検定が使えるかを最初に考えます。

パラメトリック検定が使えないときにノンパラメトリック検定を使うという流れになります。

ノンパラメトリック検定【精度はあまり高くないけど広く使われる】

χ2検定はノンパラメトリック検定の代表的なものです。

血液型などの名義尺度やガンのステージといった順位尺度のデータは正規分布しませんが、ノンパラメトリック検定ならば統計検定を行うことができます。

なお、先ほど分析精度はパラメトリック検定のほうが高いので、統計検定ではパラメトリック検定が使えるかがまず判断されると言いました。

しかし、ノンパラメトリック検定にもメリットはあります。

例えば、数値データの間隔尺度・比率尺度でもきれいな正規分布にならないこともあります。

このような場合、パラメトリック検定では分析できませんが、ノンパラメトリック検定なら分析できます。

そのため、ノンパラメトリック検定のほうが分析の適用範囲は広いです。

また、データが少ない場合は分布が安定しないため、ノンパラメトリック検定で計算したほうが検出力が高くなります。

まとめ| 練習問題

まとめとして、今回学習した内容を踏まえて、練習問題を作成しましたので１つ１つ確認してみましょう。

問題の概要は以下の通りです。

では早速、問題を解いていきましょう。

問題①：帰無仮説と対立仮説

問題

降圧薬の投与前と1週間投与後のデータがあったとします。

降圧薬の効果についての帰無仮説と対立仮説、“投与前-投与後"のデータに対応する母集団母平均 $μ$ について正しいものを選んでください。

1. 帰無仮説を$\mathrm{H}_{0}$ : $\mu<0$，対立仮説を$\mathrm{H}_{1}$ : $\mu=0$ とする。
2. 帰無仮説を$\mathrm{H}_{0}$ : $\mu>0$，対立仮説を$\mathrm{H}_{1}$ : $\mu=0$ とする。
3. 帰無仮説を$\mathrm{H}_{0}$ : $\mu<0$，対立仮説を$\mathrm{H}_{1}$ : $\mu>0$ とする。
4. 帰無仮説を$\mathrm{H}_{0}$ : $\mu=0$，対立仮説を$\mathrm{H}_{1}$ : $\mu>0$ とする。
5. 帰無仮説を$\mathrm{H}_{0}$ : $\mu=0$，対立仮説を$\mathrm{H}_{1}$ : $\mu<0$ とする。

解説

まず、帰無仮説は効果がないとする仮説なので、「降圧薬の投与前後で血圧に変化はない」となります。

そのため、「μ = 0」となりますので、dかeに選択肢が絞られます。

次に、μが正の値と負の値のどちらを取るかの判断となります。降圧薬の効果を検討するということは、投与前は血圧が高く、投与することで血圧が下がるという方向性が仮定されます。

投与前のほうが値が大きいことより、投与前-投与後=正の数値となるため、「$\mu>0$」が正しいとなります。

よって、dが正しいものとなります。

似た問題は2019年11月に出題されています。帰無仮説と対立仮説の意味はしっかり押さえておきましょう。

問題②：有意水準

問題

有意水準を $0.05$  と定めて検定を行った結果、$p$ 値が $0.09$ となりました。この結果は有意と言えますか。

解説

$p$ 値が有意水準より大きいため、「有意ではない」です。

ただし、だからといって帰無仮説のほうが正しいというわけではありません。

あくまでも、対立仮説と帰無仮説のどちらが正しいのか分からないという状態です。

そのため、研究方法を見直して、再度実験或いは調査を行い、仮説検定するということになります。

この記事では検定に受かることよりも基本的な知識をまとめる事を目的としていますが、統計検定2級の受験のみを考えるともう少し難易度が高い問題が出るかと思います。

このことは考え方の基礎となります。

問題③：検出力の求め方

問題

標本数 $10$、標準偏差  $6$ の正規分布に従う $\mathrm{H}_{0}: \mu=20,  \mathrm{H}_{1}: \mu=40$ という2つのデータがあるとします。

検出力を求めてください。

なお、有意水準は $5%$ とします。

解説

まず帰無仮説について考えます。

標準正規分布の上側 $5%$ の位置の値は  $1.64$ となります。

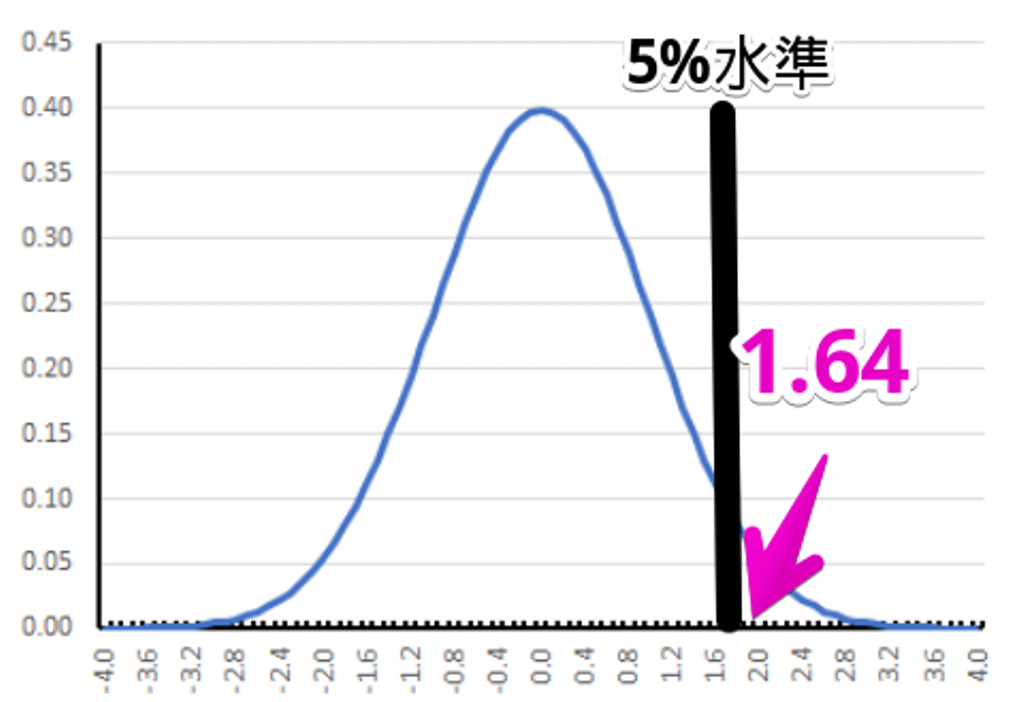
このときの  $\bar{x}=1.64 \times \frac{6}{\sqrt{10}}=3.11$のため、帰無仮説の分布の上位 $5%$ の値は $40-3.11 = 36.89$ となります。

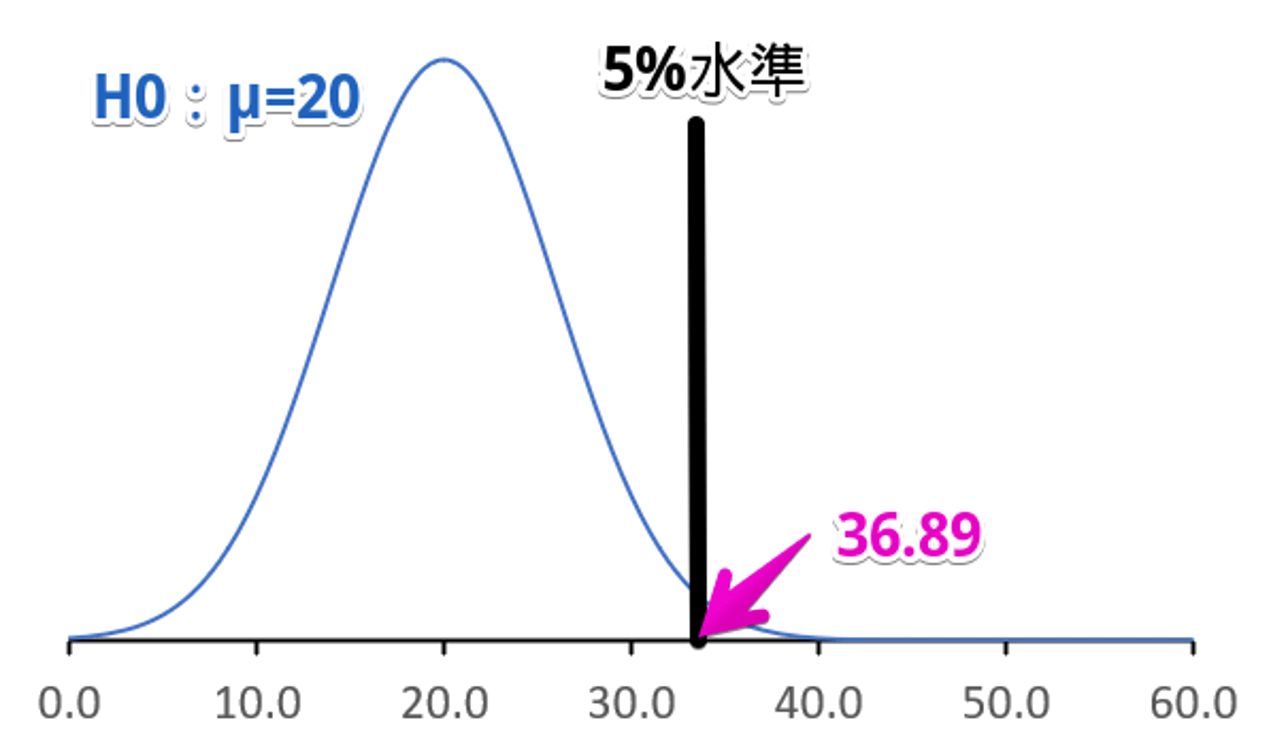
よって、標本平均が $36.89$ よりも大きいとき帰無仮説を棄却することができます。

次に、対立仮説のもとで考えましょう。

$\bar{x}=36.89$ となるときの標準正規分布の値は $\frac{36.89-40}{\frac{6}{\sqrt{10}}}=-1.64$  です。

このときの確率は、$5%$ です。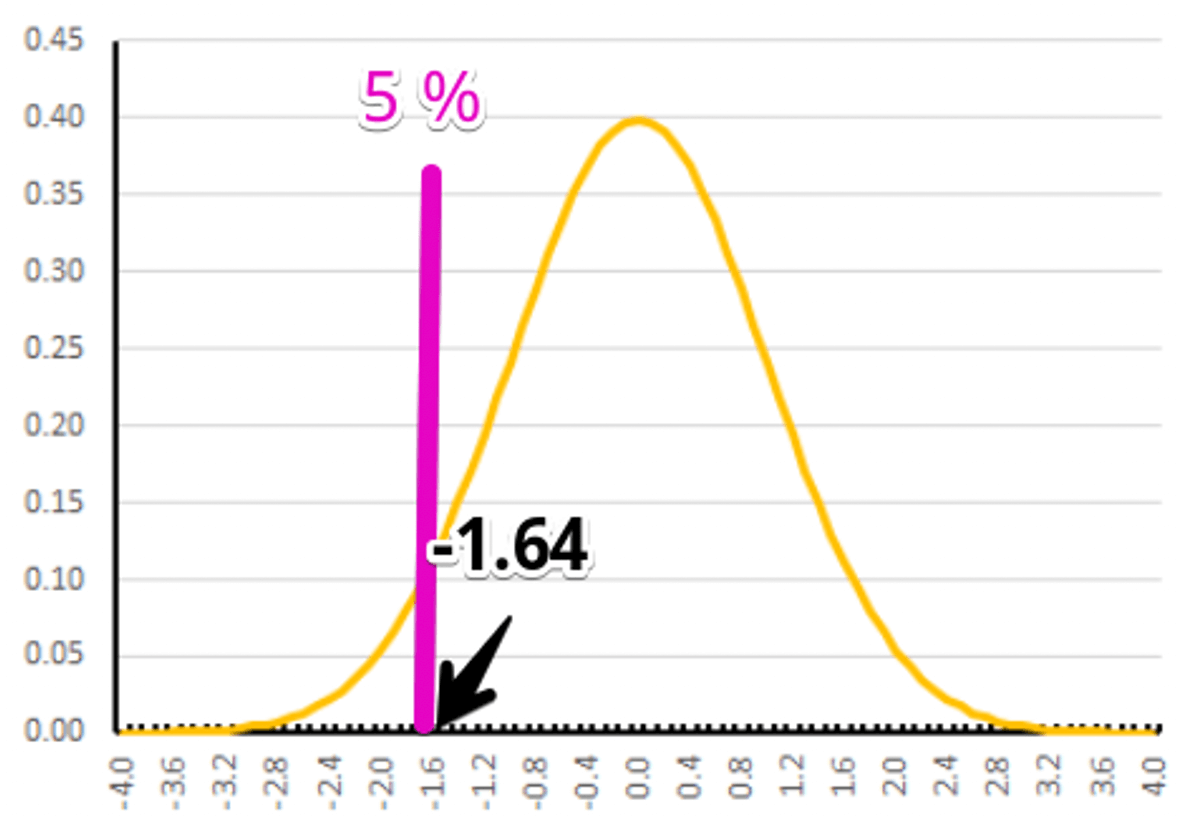

検出力とは $1-β$、すなわち帰無仮説が正しくないときに、帰無仮説を正しく棄却する確率のことです。よって、$1-0.05 = 0.95$ となります。

このタイプの問題は過去にも出題されています。

問題④：効果量

問題

降圧薬Aの効果を調べる実験を行ったところ $p$ 値は $0.05$ となり、降圧薬Bの効果を調べる実験を行ったところ $p$ 値は $0.01$ となりました。

降圧薬Bのほうが降圧薬Aよりも効果が大きいと言えますか。

解説

言えない。

例えば、降圧薬Bの実験参加者のほうが降圧薬Aの実験参加者より人数が多かったとしたら、中心極限定理よりこのような現象は起こりうるからです。

降圧薬Bのほうが降圧薬Aよりも効果が大きいかを調べるためには、①効果量を調べる、②降圧薬Aと降圧薬B、プラセボの3条件を比較する実験を行う必要があります。

今回は以上となります。