推測統計について

こんにちは。産婦人科医のとみーです。（Twitter：@obgyntommy）

本記事では推定統計について、特にデータの特徴やグラフの見方について解説していきます。

対象としては、統計検定2級の取得を目指している方、または資格取得に限らず統計の基本的な知識を学びたい方に向けた記事となります。

統計には得られたデータの特徴を分かりやすくまとめる記述統計と、得られたデータから大元の集団の特徴を推測する推測統計があります。

推測統計には、以下の2つの役割があります。

　推定統計の役割

本記事ではこのうち、推測統計の「推定」についてお話していきます。

では早速みていきましょう。

母集団と標本の関係

例えば、関東地区の視聴率を知りたいとします。

しかし、関東地区には約2,000万世帯の人たちが住んでいます。

全ての世帯の視聴データを集めるのは不可能です。

そのため、関東地区に住んでいる人のなかからランダムに選ばれた2,700世帯が見たテレビ番組を元にして、視聴率は計算されます。

この計算は、2,700世帯のうちどのくらいの割合がそのテレビ番組を見たかというのが、約2,000万世帯のテレビ番組を見た割合を反映しているという考えの元に行われます。

関東地区に住んでいる約2,000万世帯が母集団で、ランダムに選ばれた2,700世帯が標本（あるいはサンプル）です。

基本的に母集団は莫大なデータです。

そのため、母集団の一部である標本を調べることで母集団の特徴を調べます。

4つの標本抽出法とは：適当に実験参加者を集めればデータを取れるわけではない

母集団から標本を集めるにあたり、適当にしてはいけません。

万が一、特定の人からデータを集めるということになってしまったら、偏った特徴のデータばかり集まるからです。

例えば先の関東地区の視聴率であれば、適当にデータを集めた結果、偶然にも高齢者世帯が多かったとしたら、おそらく子ども向けのアニメ番組の視聴率は低く出るでしょう。

そのため、母集団からランダムに標本を取り出す「単純無作為抽出法」が大事になります。

単純無作為抽出法は、標本の集め方の基本です。

単純無作為抽出とは、母集団の全ての要素を対象として無作為抽出する方法である。

無作為抽出の最も基本的な方法で、もっとも単純な方法である。

単純無作為抽出法以外では、「標本抽出枠に何らかの規則性がないか」とか「全校生徒の男子と女子の比率」などの様々な情報が必要になるのとは違い、単純無作為抽出法は「抽出枠」の情報さえあれば行うことが出来、抽出枠の大きさが小さい場合はこの手法を使うのが最も楽である。

しかし、抽出枠が大きい場合は非常に手間と時間がかかるので、「層化」や「多段抽出」を行った方が楽である。

系統抽出とは違い、隣り合った要素同士が選ばれたり、3個以上連続した要素が選ばれる可能性がある。住民の意識調査などでは、同じ世帯の人は同じ意見を持つ可能性が高いので、同じ世帯から複数の人が抽出される可能性が有ることは、デメリットになる。

ただし、抽出枠が非常に大きい場合は、隣り合った要素同士が選ばれる可能性はほとんどないので、あまり気にされない。

» 無作為抽出法【Wikipedia】

ランダムに標本を集めなかったことで問題が起きた事例は、歴史上においても存在します。

それは、1936年にアメリカで行われたルーズベルトとランドンのどちらが大統領に選ばれるかという予想です。

皆さんは以下のAとBでどちらのほうが、正しい大統領を予想できたでしょうか。

答えは、Bのアメリカ世論研究所です。

アメリカ世論研究所では、大統領選挙の投票権を持つ人たちを「収入中間層・女性」「収入下位層・農村部・男性」のようにいくつもの重ならないグループに分けて、各グループに対して決まった割合で標本を抽出するという科学的な方法を行いました。

一方リテラリー・ダイジェストでは、自社の雑誌の購読者や、電話や自動車保有者の名簿を使って世論調査を行いました。

1936年は世界恐慌の真っただ中のため、雑誌を定期的に購読している人や、自動車や電話を持っている人はほとんどいません。

そのようなことができるのは、一部の富裕者だけです。

このように、リテラリー・ダイジェストでは標本の集め方に偏りがあったため、誤った予想となったのです。

この世論調査の結果から、母集団から標本を取り出すのはランダムであることが非常に重要なことが伺えます。

標本の抽出方法には、他にも以下の4種類の標本の集め方があります。

系統抽出法【一番目の対象者はランダムに選び、残りの対象者は〇番目置きに選ぶ】

系統抽出法とは、標本の対象者に通し番号を付け、一番目の対象者はランダムに選び、残りの対象者は〇番目間隔ごとに選ぶ方法です。

単純無作為抽出法と比べると、実験参加者を集めるのに手間がかからないというメリットがあります。

しかし、例えば名簿が男女で並んでいて、偶数番目の対象者を選ぶとしたら、特定の性別しか抽出できません。

このように、名簿の並びに法則性があると、抽出する標本に偏りが生じる恐れがあります。

層化抽出法：あらかじめ分けた層から対象者を集める

層化抽出法とは、母集団の特徴を考慮した部分集団（層）に分け、母集団の特徴をできるだけ保てるように標本を抽出する方法のことです。

例えば、男女の比率が3:2の中学校で意識調査を行う場合、男女比率が3:2となるようにデータを集めます。

母集団の特徴の通りに標本を抽出するため、母集団の推測精度が高いというメリットがあります。

しかし、層化抽出法を行うには事前に母集団の構成情報などの特徴を知らなければいけません。

クラスター抽出法：母集団を小集団に分け、無作為に小集団から対象者を集める

クラスター抽出法は、以下の3段階の方法からなります。

　クラスター抽出法

例えば日本の中学生の平均身長を調査する場合ならば、各中学校がクラスターとなります。

全国の中学校からランダムに100校選び、その選んだ100校の中学校の生徒の身長のデータを集めるといった具合です。

今回の例で考えると、中学校名などのクラスターの情報があれば時間や手間をあまりかけずに対象者を抽出することができます。

ただ、同じクラスター（今回の例であれば同じ中学校）に属する対象者は似た性質を持っていることが多いです。

そのため、万が一女子校が多く選ばれた場合、結果が歪んで平均身長が低くなってしまう恐れがあります。

多段抽出法：何段階も層化抽出を行う方法

多段抽出法では、複数の段階を経て標本の抽出を行います。

例えば、日本の中学生の平均身長を調査するならば、まず全国の中学校からランダムにいくつかの都道府県を選び、都道府県からランダムに市町村を選び、さらにその市町村の中学校のなかから対象者をランダムに選ぶといった具合です。

対象者がある程度地点ごとにまとまっているため、単純無作為抽出法と比べると移動や時間などのコストを節約することができます。

ただ、標本サイズがあまり大きくない場合、標本に偏りが生じる恐れがあります。

統計的推測のベースとなる考え方：どうして集めた標本から母集団の特徴が分かるか

視聴率や選挙の当選などのように、一部の標本データから分かったことで全体の特徴を判断することを統計的推測と言います。

統計的推測のベースには、大数の法則と中心極限定理という2つの考え方があります。

　統計的推測のベース

大数の法則【サンプル数が多いほど、標本の平均は母集団の平均と等しくなる】

一言でいえば大数の法則とは、充分な数の標本を調べれば、その標本集団は母集団の傾向・特徴と同じになるということです。

このコンテンツの最初にお話した関東地区の視聴率がまさにこれです。

大数の法則は、元々は確率論の定理です。

ある確率 $p$ で起こる事象があるとします。

コインでもサイコロでもそうですが、実際にはランダムに目が出るため、きれいに確率 $p$ となることはありません。

しかし、その試行回数を増やすほど、実際に起こる目が出る確率は理論値である $p$ に近づいていきます。

サイコロの目で考えていきましょう。

理論的にはサイコロは全ての目が $1/6$ の確率で出るけど、実際にしてみるとどうなるでしょうか。

実際にサイコロを10回投げてみた結果、以下の図の通りになりました。

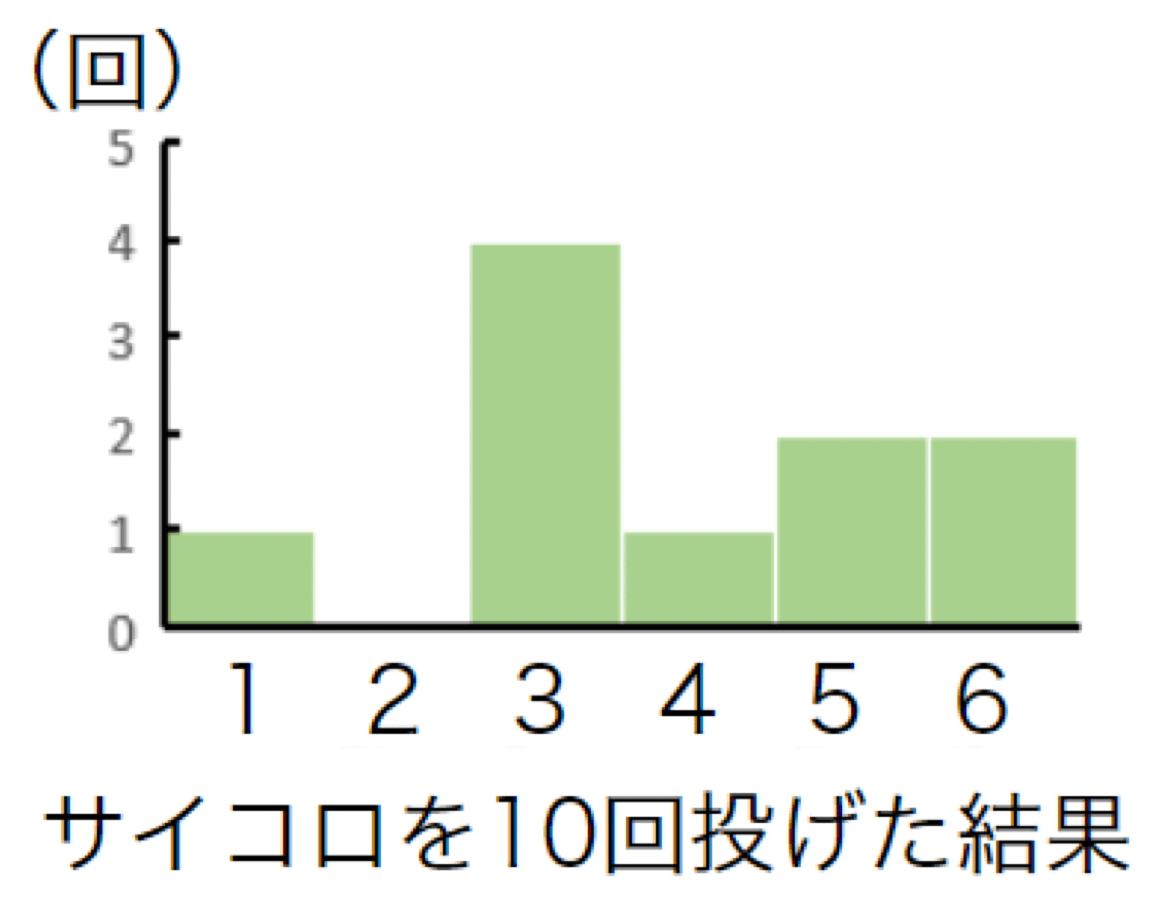
次に、サイコロを20回投げてみると、以下の図の通りになりました。

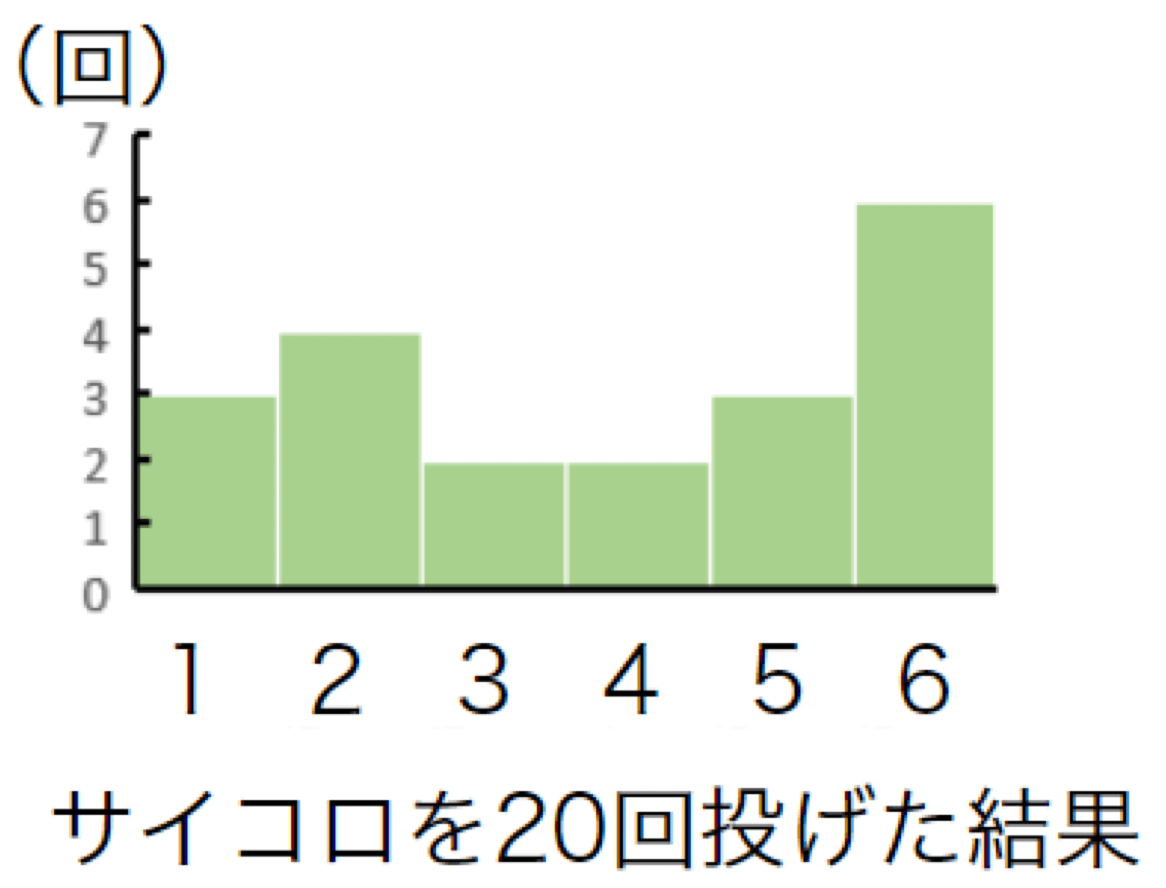
さらに、サイコロを50回投げてみると、以下の図の通りになりました。

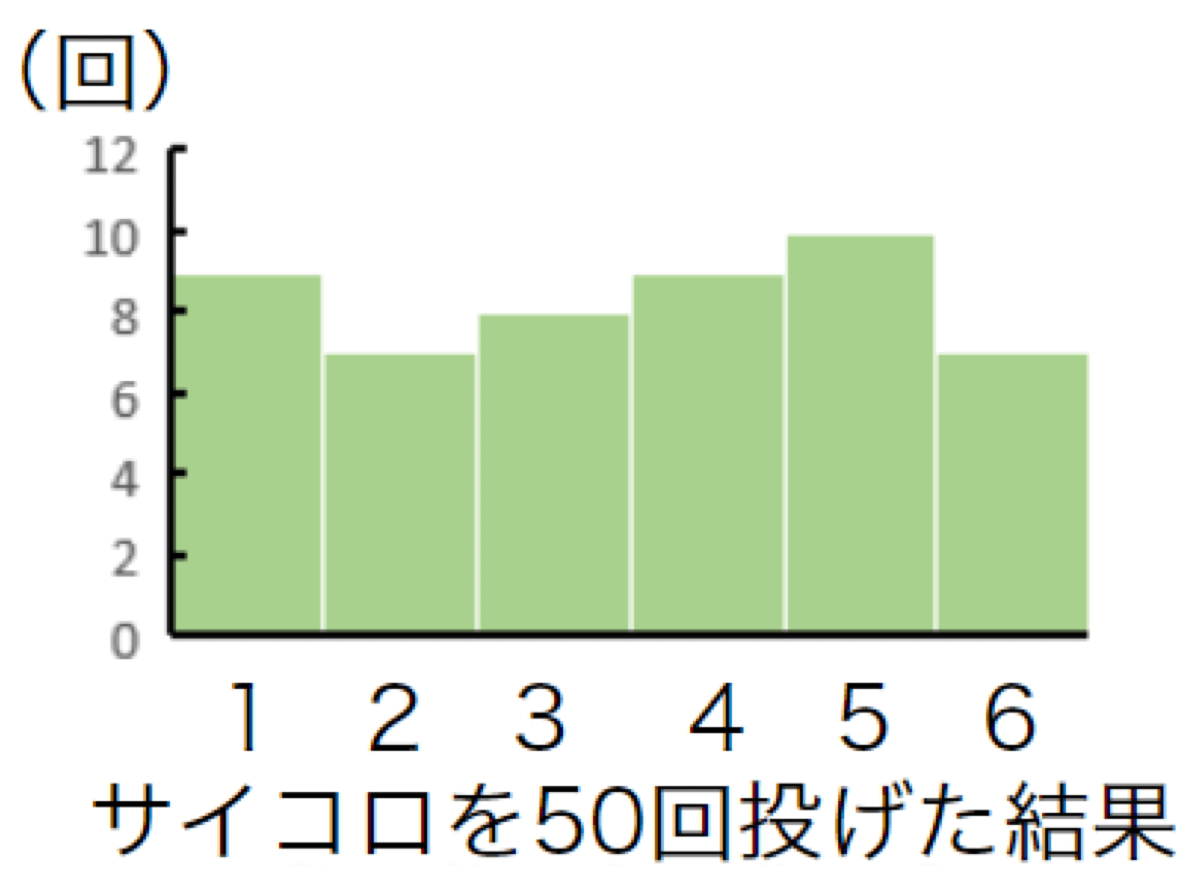
 徐々に、全ての目が同じぐらい出ていることが実感できると思います。

サイコロはどの目も $1/6$ の確率で出ることが決まっています。

しかし、実際の多くのデータはどのくらいの確率で出るかは神のみぞ知る所です。

そのため、多くの回数をこなせば理論値が出るという大数の法則に従って、標本集団から全体の母集団を推測しようとするのです。

今回の例はサイコロだから全て同じ確率でした。

しかし、人の身長のデータを扱った場合、平均身長ほど出る確率は高く、非常に高い身長あるいは非常に低い身長が出る確率は低くなります。

標本数が少なければ、偶然にも非常に高い身長・低い身長のデータが混じってしまうこともあるでしょう。

しかし、標本数が多くなるほど、平均身長に近いデータがたくさん集まるのが自然ですよね。

そのため、標本が多いほど、その標本集団は母集団の傾向・特徴と同じになると言えるのです。

中心極限定理【サンプル数が多いほど、正規分布に近づいていく】

中心極限定理とは、母集団がどんな分布であったとしても、標本集団が大きいほど標本の平均値の分布は正規分布を取るというものです。

先ほどと同様にサイコロでイメージしてみましょう。

まず、サイコロ1個を50回ほど転がした目の分布図は以下のようになりました。

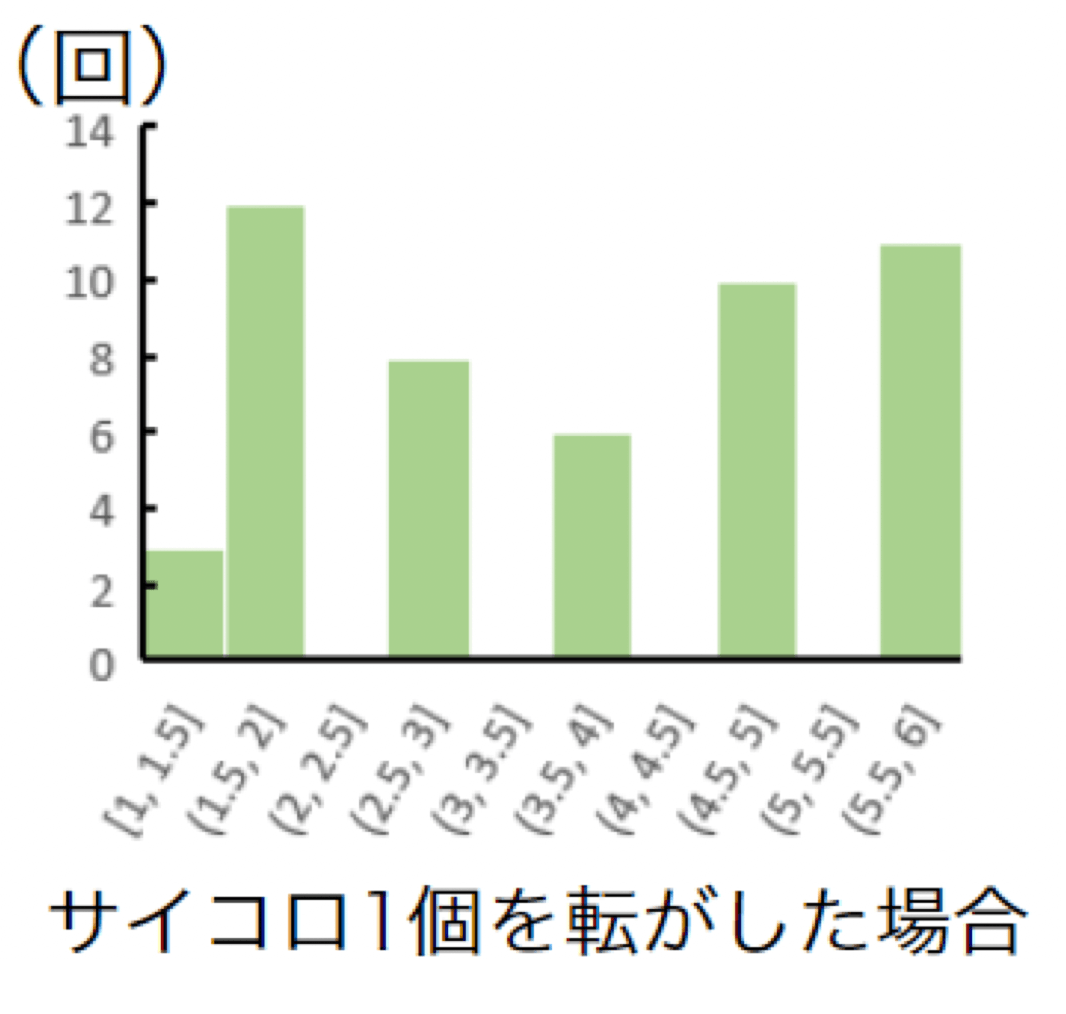 次に、サイコロ2個を50回ほど転がした目の平均値の分布図は以下のようになりました。

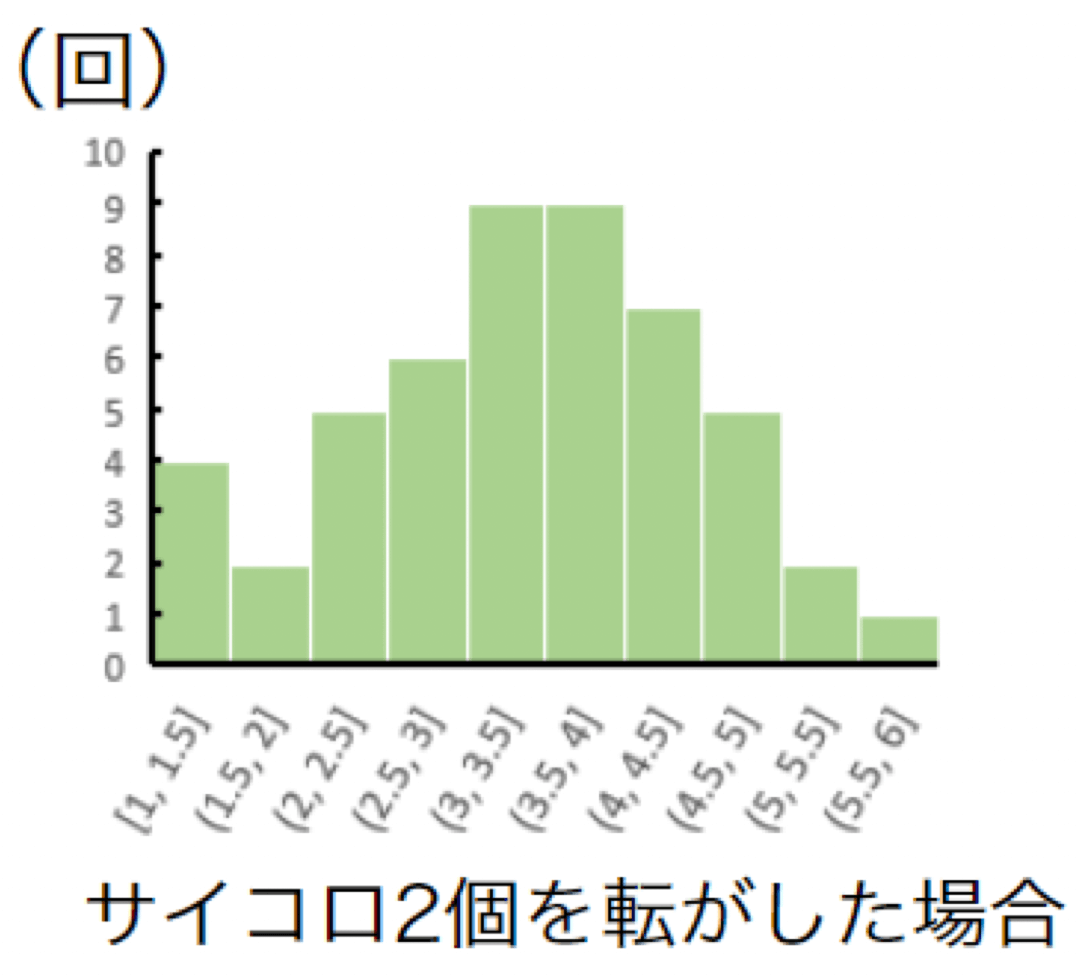
そして、サイコロ10個を50回ほど転がした目の平均値の分布図は以下のようになりました。

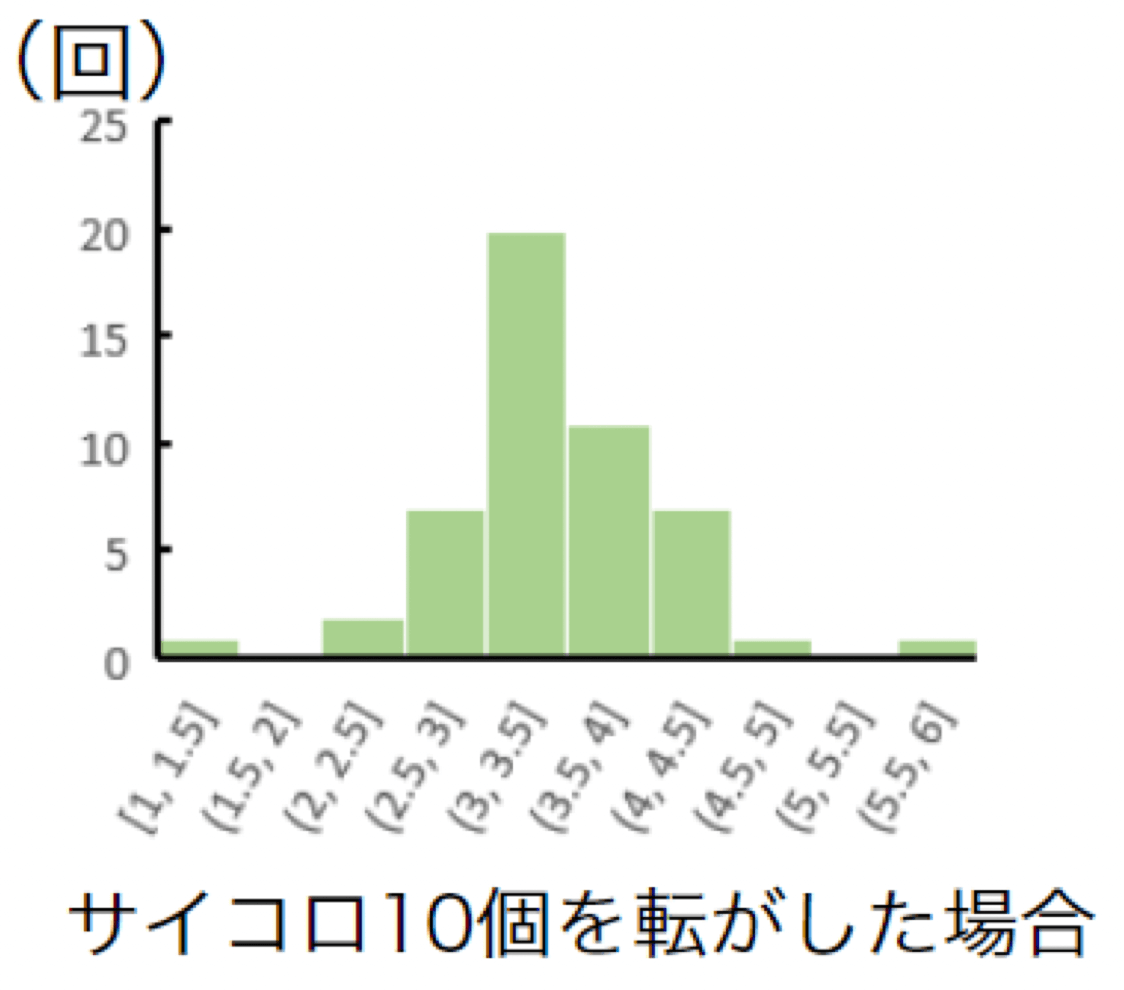
サイコロの数が増えるほど、裾野が狭い正規分布になることが分かります。

標本の平均値が正規分布になるのであれば、母集団の平均からの誤差について確率的な推測を行えます。

その結果、母集団全てではなく一部の標本の調査でも、ある程度の幅をもって信頼できる結果が得ることができるのです。

実際に標本から母集団を推定してみよう

以下のような架空の飲食店の美味しさの評価があったとします。

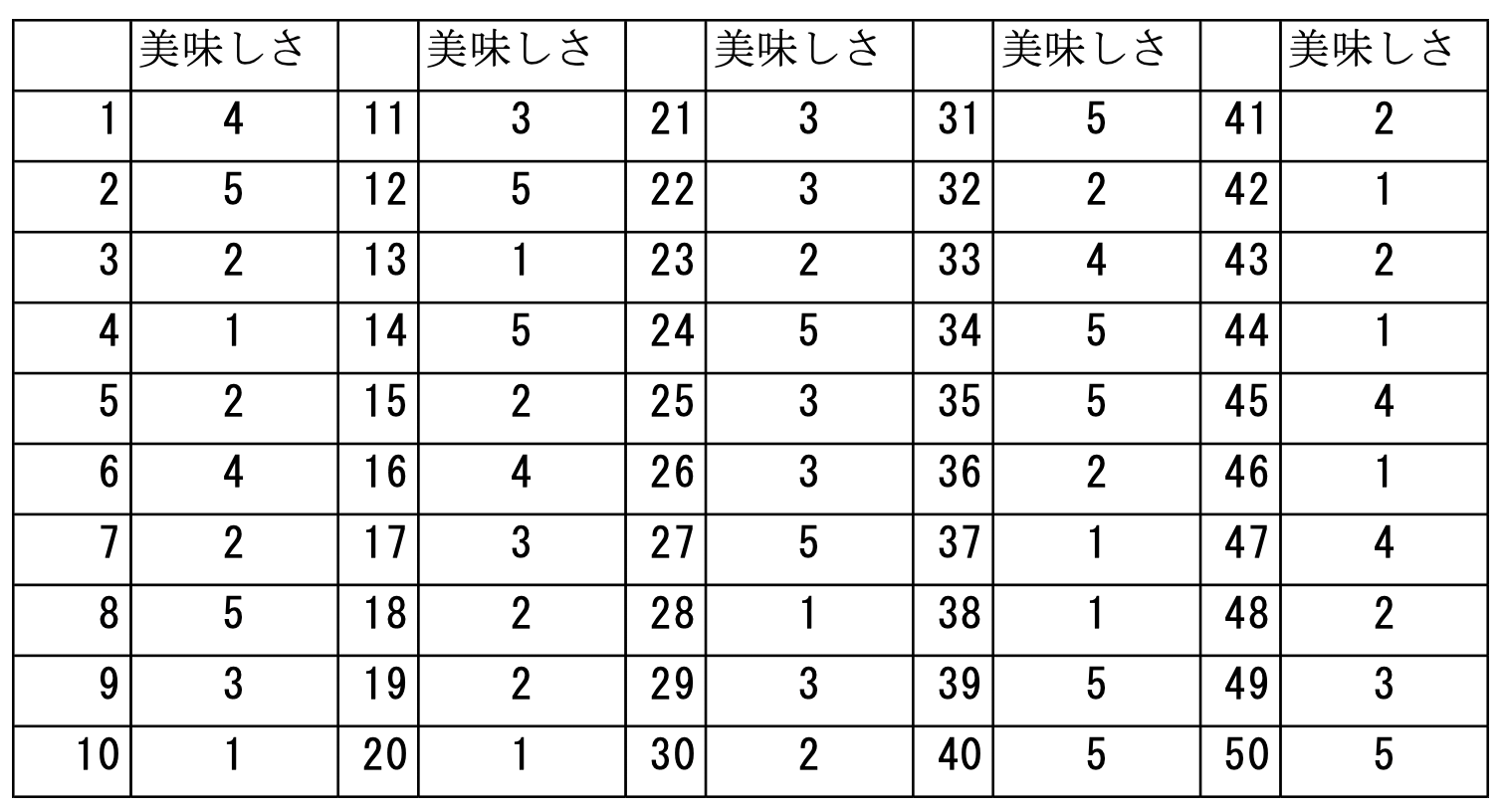
 この標本データの平均値と分散は、それぞれ 2.94 、2.14 です。

これからこの標本データを元に、母集団の特徴を推定してみましょう。

母平均を求めよう

母集団の平均のことを母平均と言います。

大数の法則「充分な数の標本を調べれば、その標本集団は母集団の傾向・特徴と同じになる」を思い出しましょう。

これより、標本の平均は母平均と同じとみなすことができます。

よって、上記の表の平均値の2.94が母平均となります。

「本当に標本の平均が母集団全体の平均とピッタリ一致するのか？」と思われた人もいると思います。

その通りで、母平均の求め方には先ほどの2.94のようにピンポイントで推定する（点推定）と、このぐらいの確率でこの幅の間に母平均がある（区間推定）の2種類があります。

次の項で説明する母集団の分散、すなわち母分散が分かっている場合、区間推定は以下の式から求めることができます。

$$\bar{x}-1.96 \times \sqrt{\frac{\sigma^{2}}{n}} \leq \mu \leq \bar{x}+1.96 \times \sqrt{\frac{\sigma^{2}}{n}}$$

この1.96という数字には実は意味があります。

先ほど中心極限定理「標本集団が大きいほど標本の平均値の分布は正規分布を取る」のお話をしました。

つまり、母平均も以下の分布内にあるということになります。

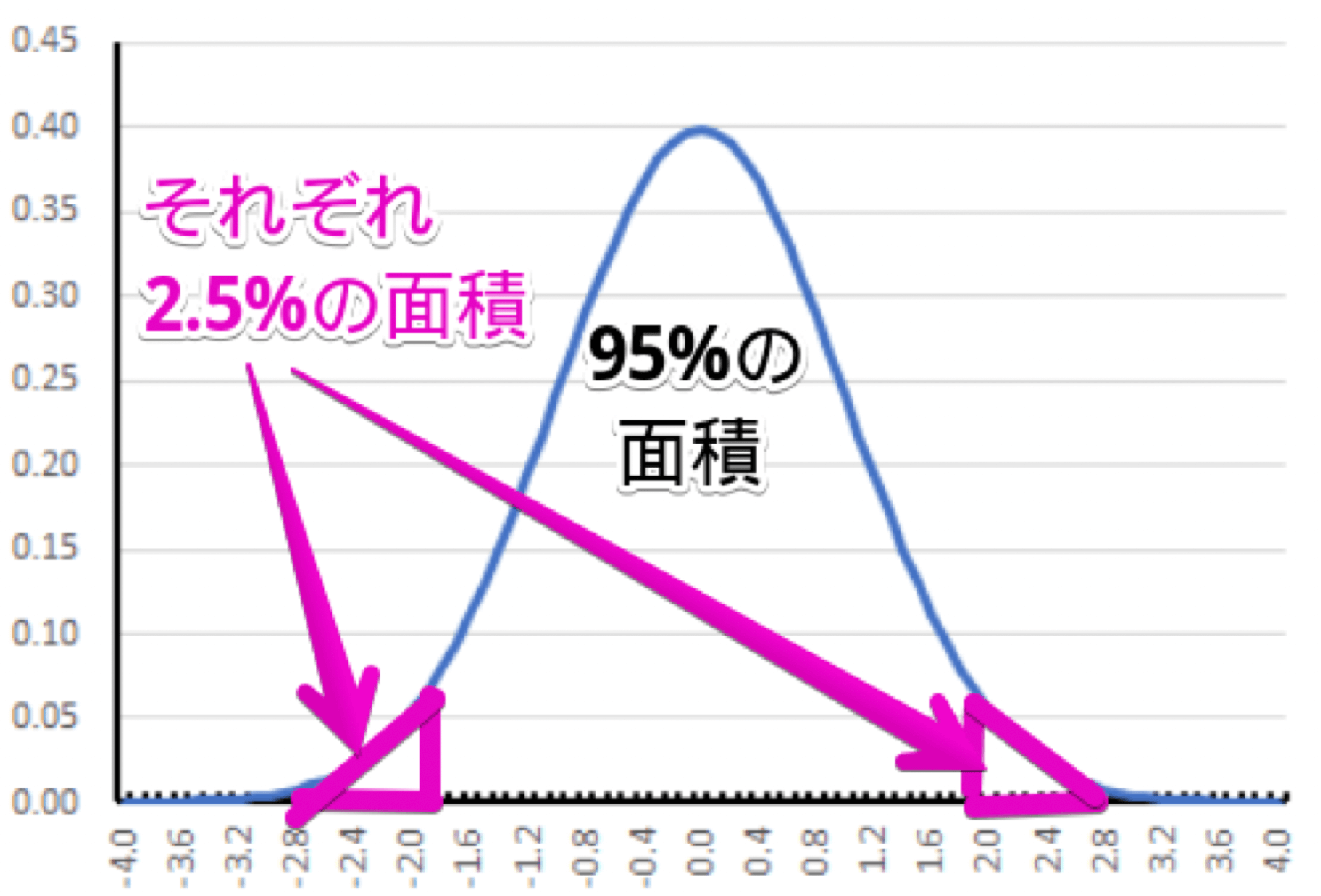
そして、95%の面積にあれば、95%の確率で母平均が含まれる範囲にあるということになります（なお、このことを95%信頼区間と言います）。

この95%の面積のときの $x$ 軸の値が $±1.96$ なので、$1.96$  をかけるのです。

ただ母平均が分かっていない場合、母集団の分散も分かっていないことが多いです。

そのため、実際は上記の式ではなく以下の式が用いられることが多いです。

母分散が分かっているときとの違いは、以下の2点です。

$1.96$ ではなく、$t_{\frac{a}{2}}(n-1)$ を用いるのは、母分散が分からない、すなわち分布の形が分からないためです。

そのため、標準正規分布と似た形の $t$ 分布というのを使うことになるのです。

ここで、新しい不偏分散という言葉が出てきました。

ここからは、不遍分散について丁寧に説明していきたいと思います。

母分散や不偏分散を求めよう

母分散とは、先ほども少しお話ししましたが、母集団の分散のことです。

大数の法則より標本の平均は母集団の平均とみなしてよいと言いました。

しかし、分散に関しては、標本数が十分に大きくなければ、標本の分散は母集団の分散よりも小さくなることが分かっています。

そこで、標本分散が母分散と等しくなるように補正したものを使うのです。

これが、不偏分散です。

不偏分散は以下の式によって求められます。

$$s^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}$$

計算の結果、不偏分散 $S^{2} = 2.18$ であることが分かりました。

そして、母分散は不偏分散を用いて計算されます。

母平均を区間推定で求めたように、母分散も区間推定で求められます。

母分散の区間推定の式は以下になります。

$$\frac{(n-1) \times s^{2}}{x 2 \text { 下側 }} \leq \mu \leq \frac{(n-1) \times s^{2}}{x^{2} \text { 上側 }}$$

先ほどの母平均のときは正規分布を元に計算していましたが、母分散の場合は $x^{2}$ と呼ばれる分布を元に計算することになります。

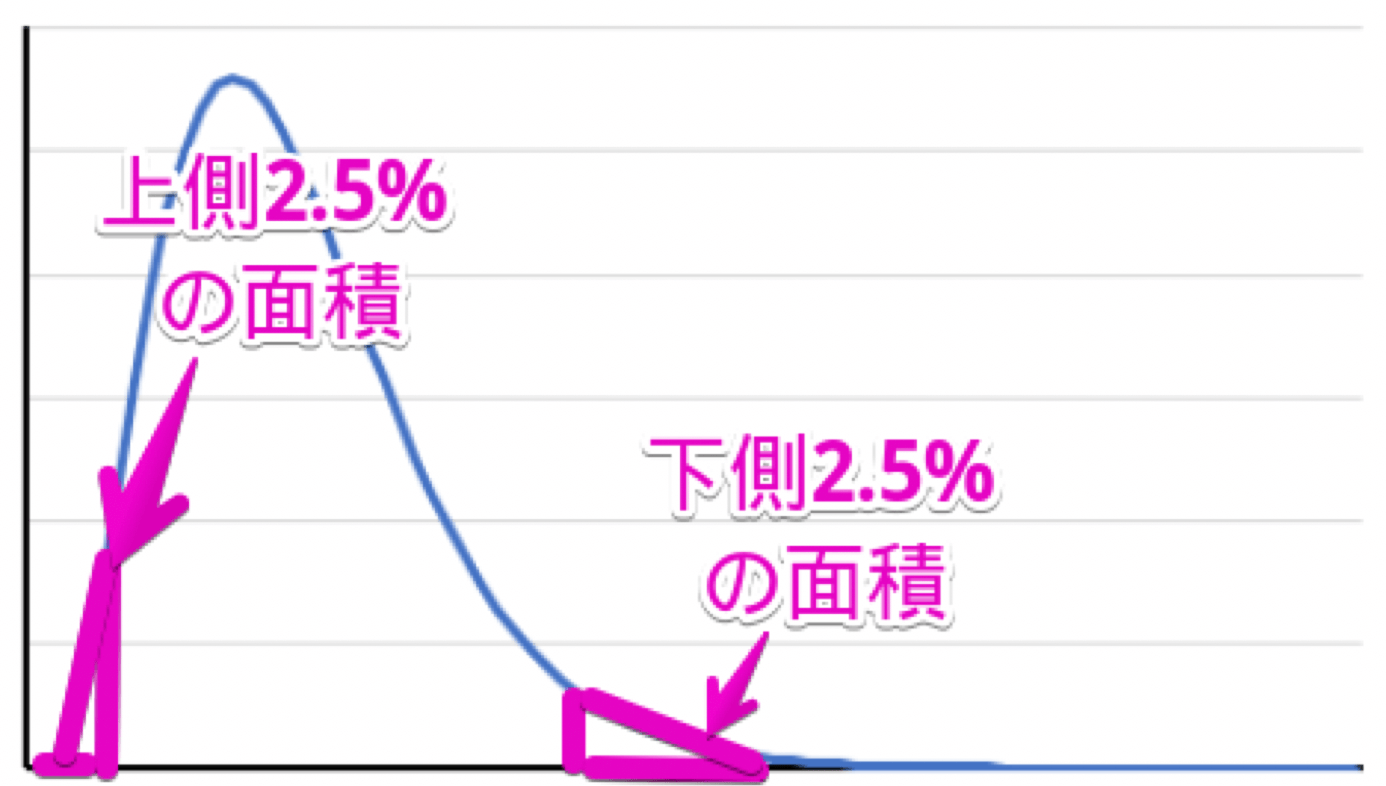
$x^{2}$ 上側や $x^{2}$ 下側というのは、分布の以下の部分になります。

$x^{2}$表に従って、値を入れて計算していきます。

今回は $n-1$  （自由度と言います：標本数から1引いたもの）が49なので、便宜的に自由度50の部分を見ていきます。

すなわち0.975の部分は32.4、すなわち0.025の部分は71.4です。すると、以下のようになります。

$$\frac{(50-1) \times 2.18}{32.4} \leq \mu \leq \frac{(50-1) \times 2.18}{71.4}$$

$$1.50 \leq \mu \leq 3.30$$

母比率とは何か

母平均、母分散と来ましたので何となく予想が付くと思いますが、母比率とは母集団においてある事象が起きる確率のことです。

母比率 $p$ は以下の式で求めることができます。 

$\hat{p}$：標本比率

ここで再び[1.96]という数字が入っているのは、中心極限定理より標本が多いときは正規分布に従うためです。

実際に、サイコロで計算してみましょう。

100回サイコロを投げたとして、1の目が30回出たとします。標本比率  $\hat{p}=30 / 100=0.3$ となります。

よって、上記の母比率の式に値を入れていくと、以下のようになります。

$$0.21 \leq p \leq 0.39$$

ここで、実際に問題を通して練習していきましょう。

まとめ| 練習問題

まとめとして、今回学習した内容を踏まえて、練習問題を作成しましたので１つ１つ確認してみましょう。

問題の概要は以下の通りです。

では早速、問題を解いていきましょう。

① 標本抽出法

問題：ある全国チェーンのマッサージサロンにて利用者アンケートを行うことになりました。以下の標本抽出法の名前は、それぞれ何でしょうか？

a： 全国の各店舗からいくつかのお店をランダムにピックアップし、そのお店の利用者全員にアンケートを行う。

b：マッサージサロン全体での利用者の年齢層別割合を考慮し、その割合の通りにアンケートを配る。

c：全国の各店舗のうちランダムに都道府県を選び、その中からランダムに利用者を選びアンケートに回答してもらう。

解説・解答

a：クラスター抽出法。クラスター抽出法には別名．集落抽出法という名前がある点に注意しましょう。

b：層化抽出法。

c：二段抽出法。多段抽出法のうち、段階が2つの場合は二段抽出法と呼ばれます。

なお、この手の問題は2019年6月、11月と出題されています。

特に、クラスター抽出法ではなく集落抽出法という名前のほうが回答だったため、別名もしっかり押さえておきましょう。

また、2019年6月はそれぞれの特徴を〇×形式で回答するという問題が出題されていました。各抽出法の特徴も併せて復習してください。

② 大数の法則と中心極限定理

問題：以下は、大数の法則と中心極限定理のどちらでしょうか。

a: 充分な数の標本を調べれば、その標本集団は母集団の傾向・特徴と同じになる

b: 母集団がどんな分布であったとしても、標本集団が大きいほど標本の平均値の分布は正規分布を取る

解答・解説

a：大数の法則。この法則があるから、標本の平均は母集団の平均と等しいとみなしてよいことになります。
b：中心極限定理。標本の平均値が正規分布になるのであれば、母集団の平均からの誤差について確率的な推測を行えます。中心極点定理の応用例としては、世論調査に必要なサンプルサイズの計算や、選挙の当選結果の予測などが挙げられます。

③ 母平均の信頼区間

問題：ある高校の2年生400人から無作為に20人取りだしたときの数学のテストの得点は以下の通りでした。

学年全体のテストの平均点の95%信頼区間を求めてください。なお、数学のテストの得点は正規分布に従うと仮定します。

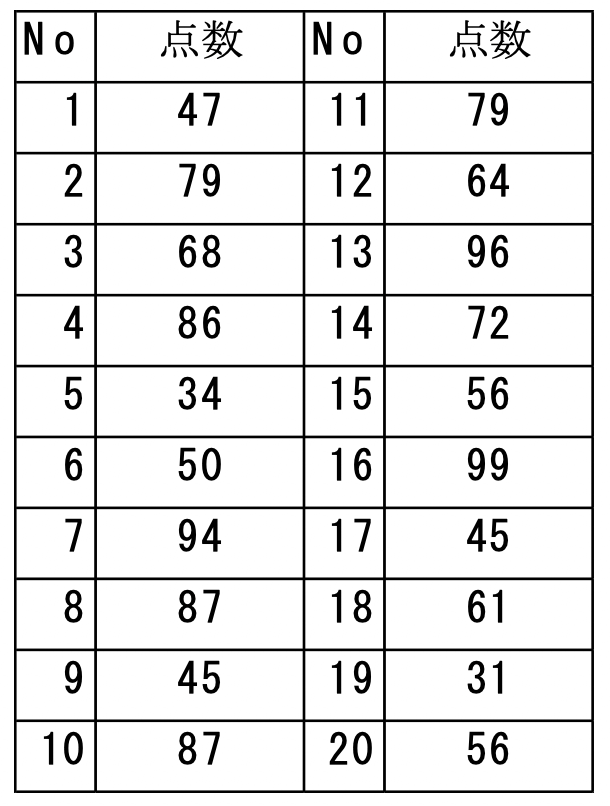
解説

母分散（この場合は学年全体でのテストの得点の分散）が分からないため、以下の式を使います。

大数の法則より、標本平均を母平均とみなしてよいため、$\bar{x}$ が式に含まれています。

計算の結果、$\bar{x}=66.8$ でした。不偏分散（$\mathrm{s}^{2}$）は以下の式から求めることができます。

$$s^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}$$

計算の結果、$s^{2}=442.0$でした。

データ数は $20$ なので $n-1=19$ となることから、$t$分布表の自由度が $19$ の所を見ていくと、$2.093$ でした。

よって、全てを式に代入すると、以下になります。

$$57.0 \leq \mu \leq 76.6$$

母分散が未知の場合の母平均の区間推定は2019年6月に出題されています。

比較的出題されやすいところであり、かつ、式に当てはめていけば解ける問題なので、確実に理解しておきましょう。

④ 母比率の信頼区間

問題

ある選挙において，100 人の投票者に出口調査を行ったところ，A 候補に投票した人は68人でした。A 候補の得票率の95% 信頼区間として，母比率の信頼区間を求めましょう。

解説・解答

信頼区間は $95%$ なので、以下の母比率の信頼区間の公式に当てはめていけば、簡単に求まります。

$$0.59 \leq p \leq 0.77$$

母比率の信頼区間はよく出題されています。必ず押さえましょう。

⑤ 母比率の信頼区間の応用

問題

ある選挙で立候補者のA氏が当選するかを、出口調査を行うことになりました。

母比率の95%信頼区間の幅を5％以内にしたい場合、何人以上を対象に調査を行う必要がありますか。なお、事前調査によりA氏の得票率は70%程度であることが分かっているものとします。

解説・解答

以下の式より、母比率 $p$ の $95%$ 信頼区間は求められます。

つまり、左右に $1.96 \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$ があるということより、

信頼区間の幅は $2 \times 1.96 \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$ と言えます。

事前調査の得票率が $70%$ で、信頼区間の幅を $5%$ 以内にしたいため、以下の式を解けば人数が分かります。

$$2 \times 1.96 \times \sqrt{\frac{0.7(1-0.7)}{n}} \leqq 0.05$$

$$\sqrt{n} \geqq 2 \times 1.96 \times \sqrt{0.7(1-0.7)} \times \frac{1}{0.05}$$

$$\sqrt{n} \geqq 2 \times 1.96 \times \sqrt{0.7(1-0.7)} \times \frac{1}{0.05}$$

$$\sqrt{n} \geqq 35.93$$

$$n \geqq 1290.8$$

今回は事前調査の得票率が分かっていましたが、もし分からない場合は母比率の信頼区間が最も大きくなる $\hat{p}=0.5$ を代入することになります。

考え方を応用する問題ですが、2019年11月にも出題されています。数式の意味もしっかり理解しておく必要があります。

今回は以上になります。