
最小2乗法と単回帰分析の関係がよく分かりません。
単回帰分析の計算方法について詳しく知りたいです。
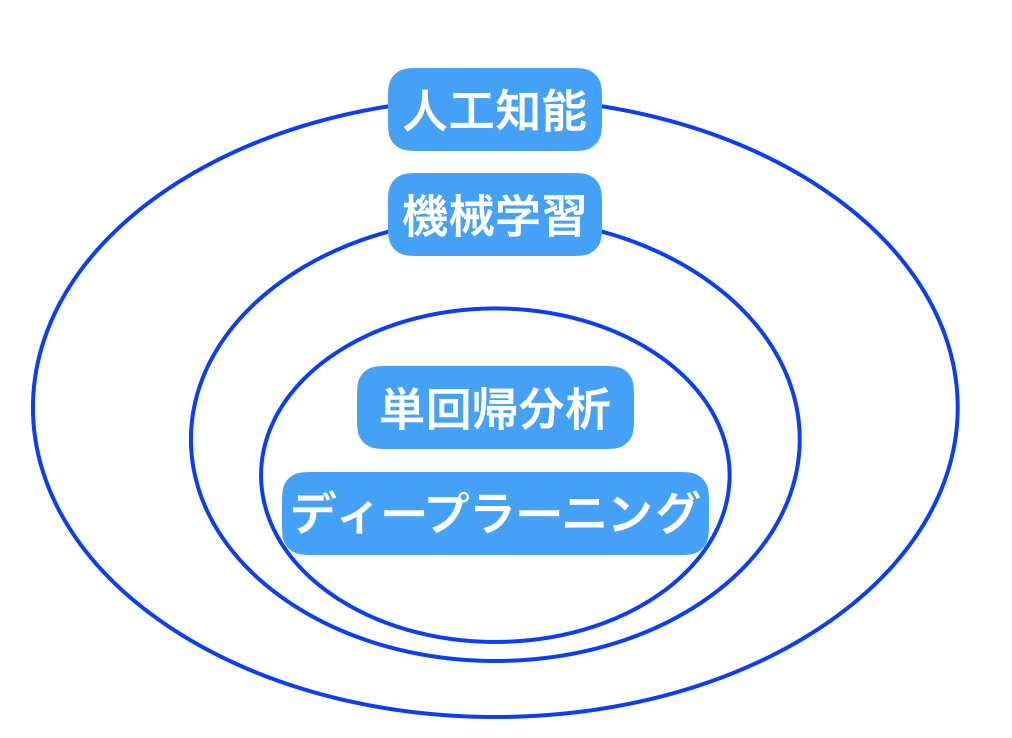
まず人工知能、機械学習、単回帰分析、ディープラーニングの相関関係は上図の様になっています。
大枠として人工知能があり、そのブレーン的役割を機械学習が果しています。
そして機械学習の手段として単回帰分析やディープラーニングが存在します。
今回は機械学習の手段のうち単回帰分析に着目して解説していきます。
本記事の学習内容
- 単回帰分析(最小2乗法)を数式を交えて理解できる様になる
それでは早速みていきましょう。
単回帰分析の求め方・使い方

単回帰分析の問題設定:部屋の家賃と広さの関係
問題設定として「家賃を予測する」という設定で考えてみましょう。
- 出力変数(家賃)を $y$
- 入力変数(部屋の広さ、駅からの距離)を $x$
と定義します。
単回帰分析では、部屋の広さや駅からの距離などの一つの予測ファクター $x$ から家賃を予測します。
単回帰分析では例えば、「部屋の広さ」のみで家賃を予測するということになります。
しかし実際には「部屋の広さ」だけではなく、「駅からの距離」など他の多数のファクターも考慮して家賃を予測したい場合もありますよね。
その様な時には単回帰分析ではなく、重回帰分析を行う必要があります。
さて、今回は単回帰分析を利用して、「部屋の家賃」と「広さ」の「相関関係を調べてみましょう。
機械学習の2つのフェーズ
機械学習のフェーズには2つの段階(フェーズ)があります。
- 学習
- 推論
この2点です。
では、学習と推論はどの様に異なるのかを図を用いて見ていきましょう。
学習
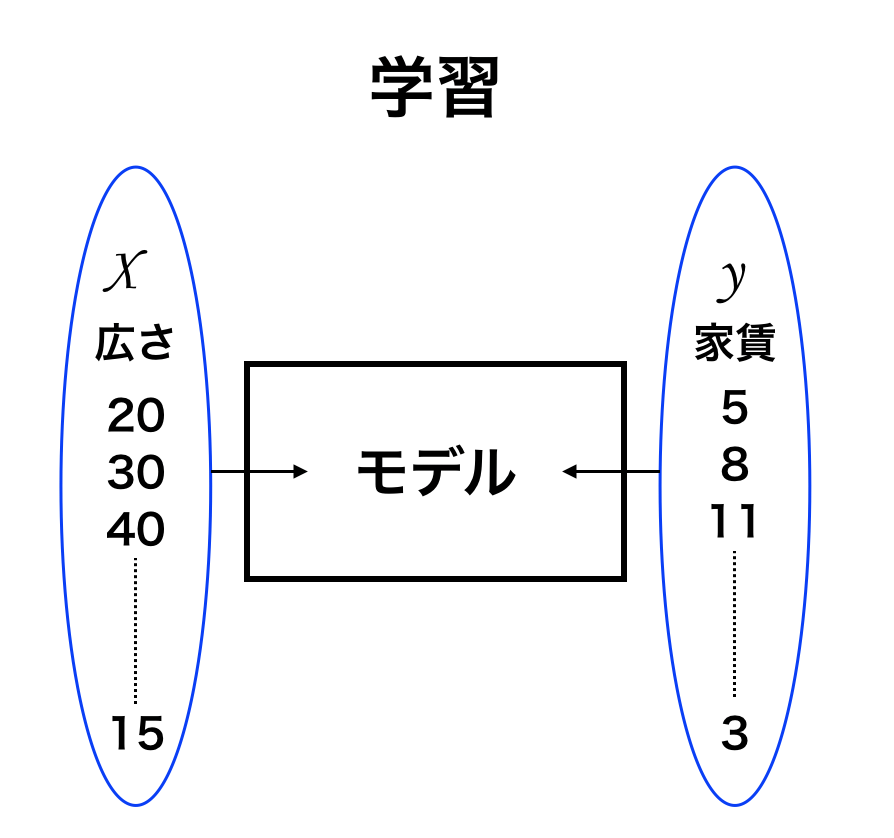
上図が学習のモデルです。
学習では以下の様に値を代入してモデルを作っていきます。
- 広さが20平米の時に家賃が5万円
- 広さが30平米の時には家賃が10万円
- 広さが40万円の時には家賃が11万円
といったようなデータを入力して、データを蓄積していきます。
まとめてみると
- $x$:部屋の広さ(平米) 20 30 40
- $y$:家賃(万円) 5 8 11
このような感じです。
このデータ入力によってモデルが完成します。
機械学習の第1フェーズとして、モデルを作るためには $x$ と $y$ に値を入れていく必要があるわけです。
推論
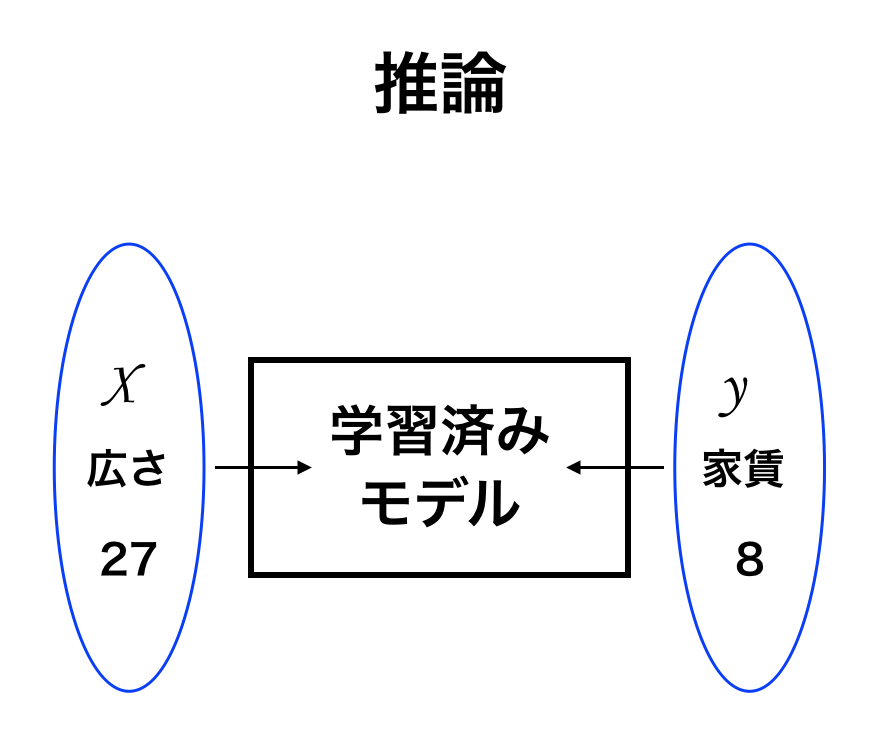
次に、機械学習の第2フェーズである推論について解説していきます。
学習によって1万のデータが蓄積されたモデルがあるとします。(上図の学習済みモデルを指しています。)
学習で得たモデル(学習済みモデル)から、広さが27平米の時には過去に学習したデータから推論して家賃を8万円と予測する。
このことを推論と言います。
この家賃の推論を行った結果、予測した家賃 8 万円のことを「予測値」と呼びます。
機械学習の第2フェーズである推論において重要なのは、
いかにして学習の「モデル」設定を行うか。
が一番のキーポイントになります。
単回帰分析のモデルを作る。

【Step1】モデル設定を行う
いよいよ単回帰分析を行なっていきましょう。
まずはモデル設定から行います。
- $x$:部屋の広さ
- $y$:家賃[/box]
とします。
部屋の広さが1平米の時に家賃2万円
部屋の広さが2平米の時に家賃が3.2万円
部屋の広さが3平米の時に家賃が6.1万円
としてモデル設定を行います。
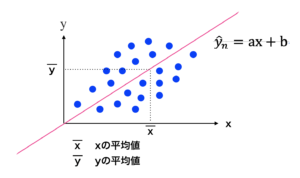
これらの点を「直線の関係になれば良いなぁ」と思いながら、プロットして繋げていきます。
ぶっちゃけこれらの点が直線になって、相関関係があるにこしたことはないですよね。
要するに直線の関係性が出来上がる事、すなわち
$$y=ax+b$$
という関係式を作る事がモデル設定を行う上での最終目標となります。
データ入力を行い $y=ax+b$ という関係が出来るとします。
この関係性はコンピューターや人工知能が決定するのではなく、人間が決定します。
$y$ の上に^がつくと、$\hat{ y }$ と表現し、これを「ワイハット」と言い、 $y$ の「予測値」でという意味があります。
モデル設定を行う際の最終目標は、 $y=ax+b$ という式を作成する事です。
そのため、モデル設定を行うためには傾き $a$ と切片 $b$ を決定する事が一番重要となります。
この $a$ , $b$ のことを「パラメーター」と言います。
データ( $x_{ 1 }$, $x_{ 2 }$, $x_{ 3 }$, $y_{ 1 }$, $y_{ 2 }$, $y_{ 3 }$ )に基づいて「適切に」パラメータ$a$,$b$ を決定することが重要になります。
この「適切」にというのはどういうことなのかは STEP2 で説明します。
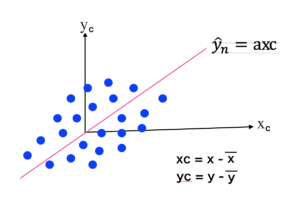
データの中心化(centering)
| $x$ | $x$ の平均値 | $Xc$ データの中心化 |
| 2 | 4 | -2 |
| 4 | 4 | 0 |
| 6 | 4 | 2 |
「データの中心化(centering)」は機械学習でよく行われる作業のため理解しておく必要があります。
上左図の様にグラフ上にデータが散らばっているとします。
このデータのばらつきを、なるべくグラフの中心に移動させることを「データの中心化(= centering )」と言います。
この中心化を行った時のグラフの $x$ 軸、$y$ 軸は centering を行った後と言う意味で、$x_{ c }$, $y_{ c }$ と表現します。
中心化を行うことでのメリットは切片の $b$ がなくなることです。
これまで求めなければならないパラメータが $a$, $b$ の2つありましたが、centering を行うことで $b$ のみを求めれば良いということになります。
それでは、データの中心化の方法はどの様にすれば求まるのでしょうか。
そのためにはデータの平均値である $\bar{ x }$, $\bar{ y }$ を求めることで、中心化を行う事が出来ます。
$\bar{ x }$:$x$ の平均値
$\bar{ y }$:$y$ の平均値
エクセルでは average で求める事ができます。
$x_{ c }=x - \bar{ x }$
$y_{ c }=y - \bar{ y }$
となります。
ここでまとめです。
前提としてデータが centering された(中心化済の)モデルには以下の式が成立します。
$\bar{ y }= ax_{ c }$
$a$:パラメーター
※ 毎回 $x$ の右下に $c$ をつけるとメンドウなので $c$ は省略することもあります。
STEP 2:単回帰分析の「評価関数」を決める。
Step1でモデルの設定を行い、モデルから「適切に」推定する式を予測する。
と表現しましたが、この「適切さ」をどの様に決定されるのでしょうか。
「適切さ」を決める方法として「評価関数(損失関数)」があります。
評価関数はディープラーニングを学ぶ方には損失関数という方が馴染みがあるかもしれません。
評価関数について、家賃と部屋の広さの関係の例えで考えてみましょう。
$y$:実際の家賃
$\hat{ y }$:予測した家賃
と定義します。
予測値の良し悪しは $y$ と $\hat{ y }$ の差で評価されます。
それはそうですよね。実際の値と予測された値がほぼ同じであればある程良いのは当然です。
そこでこの実際の値と予測値の差を2乗することで、マイナスやプラスが関係なくなり、値としても大きくなるので評価がしやすくなります。
グラフとしては以下のイメージになります。
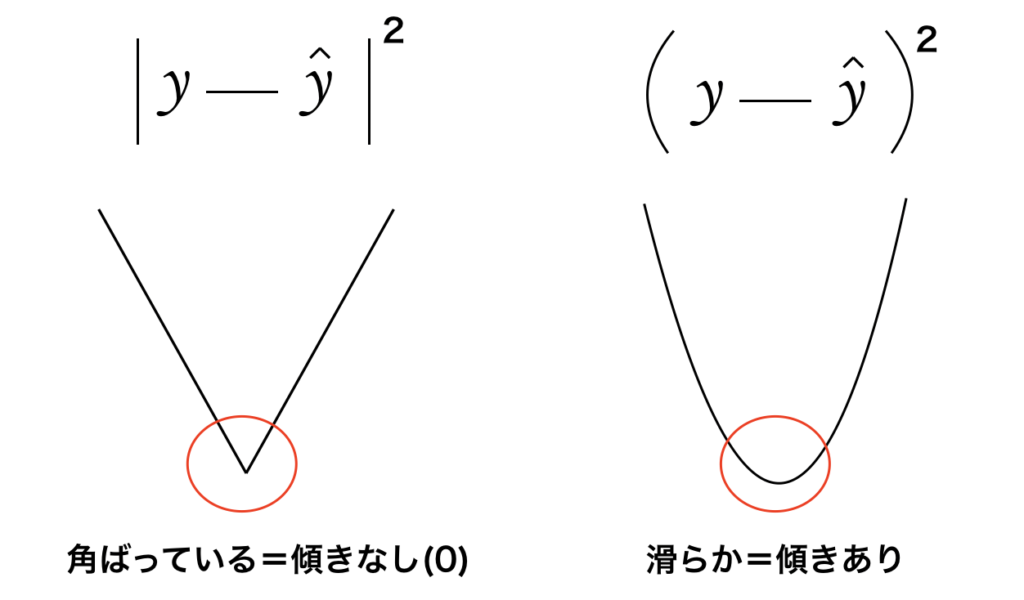
ここで出てくる批判的意見としては絶対値をつけて2乗するのでも良いのではないかという意見も出てきます。
しかし絶対値であれば上左図の様な直線のグラフになります。
一方で絶対値をつけなければ右上図の様な曲線になります。
微分を行う際には、絶対値であれば直線になるため傾きを求める事ができず、微分する際にデメリットがあるため、絶対値は使いにくいのです。
ここで、この $y$ と $\hat{ y }$ の差の値を2乗したものを「2乗誤差」と言います。式で表すと以下のようになります。
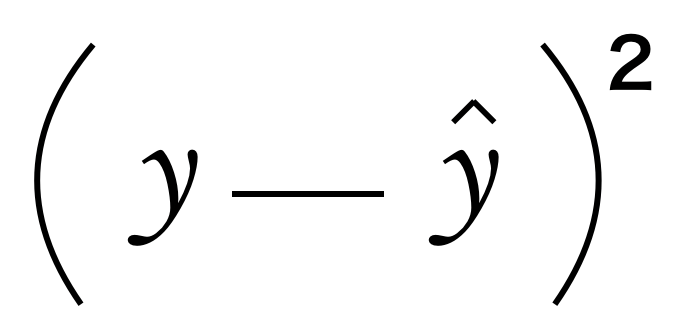
この2乗した式は評価関数(損失関数)としてどの様に使用するのかを見ていきましょう。
評価関数を表す際には文字:$\mathcal{ L }$ を使用します。
以下が評価関数の式になります。
モデルのサンプル数を $N$ 個としています。
- $\mathcal{ L }$ :評価関数(エル)
- $N$ :サンプル合計数
それでは実際に評価関数を求めていきましょう。
\(\mathcal{L}=\left(y_{1}-\hat{y}_{1}\right)^{2}+\left(y_{2}-\hat{y}_{2}\right)^{2}+\)
\(\cdots+\left(y_{N}-\hat{y}_{N}\right)^{2}=\sum_{n=1}^{N}\left(y_{n}-\hat{y}_{n}\right)^{2}\)
STEP 3 評価関数(損失関数)を最小化する。
STEP2では実際に評価関数を求めてみました。
STEP3では評価関数(損失関数)を最小化する方法について解説していきます。
というのも評価関数を最小化する = 誤差は小さければ小さいほど良いからです。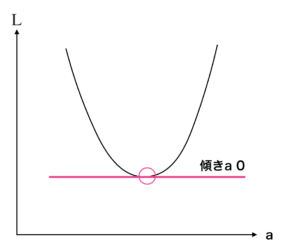
上図のグラフの縦軸が $\mathcal{ L }$ (評価関数)です。
ここで、$x$ は部屋の広さのため、変えることはできません。
そのため誤差を小さくするためにはパラメータ $a$ を変える必要が出てきます。
したがって横軸を $a$ として、$a$ と $\mathcal{ L }$ のグラフを作成し、そのうち傾きが 0 のポイントを探せば、評価関数が最小化している点を見つける事ができます。
この横軸が $a$ というのがポイントですので、覚えておきましょう。
「$傾き = 0$」
⟺ \(\frac{\partial y}{\partial a}(\mathcal{L})=0\)
⟺ \(\mathcal{L}=\sum_{n=1}^{N}\left(y_{n}-\widehat{y}_{n}\right)\)
$\frac{ \partial \mathcal{ L } }{ \partial a }=0$
上の式でもある様に、縦軸の $\mathcal{ L }$ を横軸の $a$ で偏微分しています。その値が 0 になる箇所がポイントとなります。
STEP 3-1 式変形を行う
STEP1で $\hat{ y }_{ n }=ax_{ n }$ と決定しました。
$n$ 番目の家賃の予測値を $\hat{ y }_{ n }$ すなわち $ax_{ n }$ とします。
下式の様に①に②を代入すると以下の式が成立します。
\(\mathcal{L}=\sum_{n=1}^{N}\left(y_{n}-\hat{y}_{n}\right) \ldots(1)\)
\(\hat{y}_{n}=\mathbf{a} x_{n} \ldots(2)\)
(1) に(2) を代入します。
\(\mathcal{L}=\sum_{n=1}^{N}\left(y_{n}-a x_{n}\right)^{2}\)
\(=\sum_{n=1}^{N}\left(y_{n}^{2}-2 y_{x} a x_{n}+a^{2} x_{n}^{2}\right)\)
\(=\sum_{n=1}^{N}\left(y_{n}^{2}-2 x_{x} y_{n} a+x_{n}^{2} a^{2}\right)\)
\(=\sum_{n=1}^{N}\left(y_{n}^{2}-2 x_{x} y_{n} a+x_{n}^{2} a^{2}\right)\)
\(=\sum_{n=1}^{N} y_{n}^{2}-2 a \sum_{n=1}^{N}\left(x_{n} y_{n}\right)+a^{2} \sum_{n=1}^{N} x_{n}^{2}\)
\(=\mathcal{C}_{o}-2 \mathcal{C}_{1} a+\mathcal{C}_{2} a^{2}\)
[box class="box16"]ここで以下の様に\(\mathcal{C}_{0}\)、\(\mathcal{C}_{1}\)、\(\mathcal{C}_{2}\) を定義し代入しています。
- \(\sum_{n=1}^{N} y_{n}^{2}=\mathcal{C _ {0}}\)
- \(\sum_{n=1}^{N}\left(x_{n} y_{n}\right)=\mathcal{C}_{1}\)
- \(\sum_{n=1}^{N} x_{n}^{2}=\mathcal{C}_{2}\) [/box]

ここで、$x$ と $y$ の値が上の表の様に与えられていた場合、データの中心化を行い $a$ を求めてみましょう。
\(\frac{\partial y}{\partial a}(\mathcal{L})=0\) この式に
\(\mathcal{L}=\mathcal{C}_{0}-2 \mathcal{C}_{1} a+\mathcal{C}_{2} a^{2}\) これを代入します。
\(\frac{\partial y}{\partial a}(\mathcal{L})=0\)
⟺ \(\frac{\partial}{\partial a}\left(\mathcal{C _ {0}}-2\mathcal{C}_{1}a+\mathcal{C}_{2}a^{2}\right)=0\)
⟺ \(\frac{\partial}{\partial a}\left(\mathcal{C}_{0}\right)-\frac{\partial}{\partial a}\left(2 \mathcal{C}_{1} a\right)+\frac{\partial}{\partial a}\left(\mathcal{C}_{2} a^{2}\right)=0\)
\(\frac{\partial}{\partial a}\left(\mathcal{C}_{0}\right)=0\) として代入すると
⟺ \(\frac{\partial}{\partial a}\left(\mathcal{C}_{0}\right)-2 C_{1} \frac{\partial}{\partial a}(a)+C_{2} \frac{\partial}{\partial a}\left(a^{2}\right)=0\)
式変形を行うと
⟺ \(-2 \mathcal{C}_{1} \frac{\partial}{\partial a}(a)+\mathcal{C}_{2} \frac{\partial}{\partial a}\left(a^{2}\right)=0\)
⟺ \(2 \mathcal{C}_{1} \frac{\partial}{\partial a}(a)=\mathcal{C}_{2} \frac{\partial}{\partial a}\left(a^{2}\right)\)
⟺ \(2 \mathcal{C}_{1}=\mathcal{C}_{2}\)
⟺ \(a=\frac{\mathcal{C}_{1}}{\mathcal{C}_{2}}=\frac{\sum_{n=1}^{N} x_{n} y_{n}}{\sum_{n=1}^{N} x_{n}^{2}}\)
この様な式展開で $a$ を$x$ と $y$ で表現する事が出来ました。
STEP 3-2:最適なパラメーター $a$ を求める
上図の様に評価関数に対してもっとも誤差が小さい箇所、すなわち頂点が「最適なパラメータ」となりました。
傾きを算出するためには $\mathcal{ L }$ を $a$ で偏微分を行い、0になる箇所を求めれば良いという事が分かりました。
単回帰分析:まとめ

今回は機械学習のうちの一つのツールである単回帰分析について学びました。
数式が中心でしたが、pythonのプログラミングを行う前にはまずこれらの数式を理解しておく事が重要となりますので、ぜひおさえておきましょう。
ご自身で手を動かして数式を書いてみることをお勧めします。
みなさんの知識の整理のお役に立てれば幸いです。
今回は以上とします。
