機会学習と予測モデル

こんにちわ。


今回は機械学習においてコアとなる概念である「最適化」を学ぶ事を目標として、そのために必要な知識である「予測モデル」を学習します。


この記事で「予測モデル」について学習した後に、線形モデルを使用して評価関数を作成し、最適なモデルのパラメータを決定するために勾配降下法を自在に用いる事ができる様になる、最適化を理解出来る様になる事が目標です。


※　京都大学で配布されている機械学習と数理の応用のスライドが、機械学習と予測モデルや線形モデルを理解する上で非常に役に立ちますのでご参照下さい。
» 機械学習と数理の応用【京都大学集中講義】


では早速、見ていきましょう。

機械学習における予測モデルとは

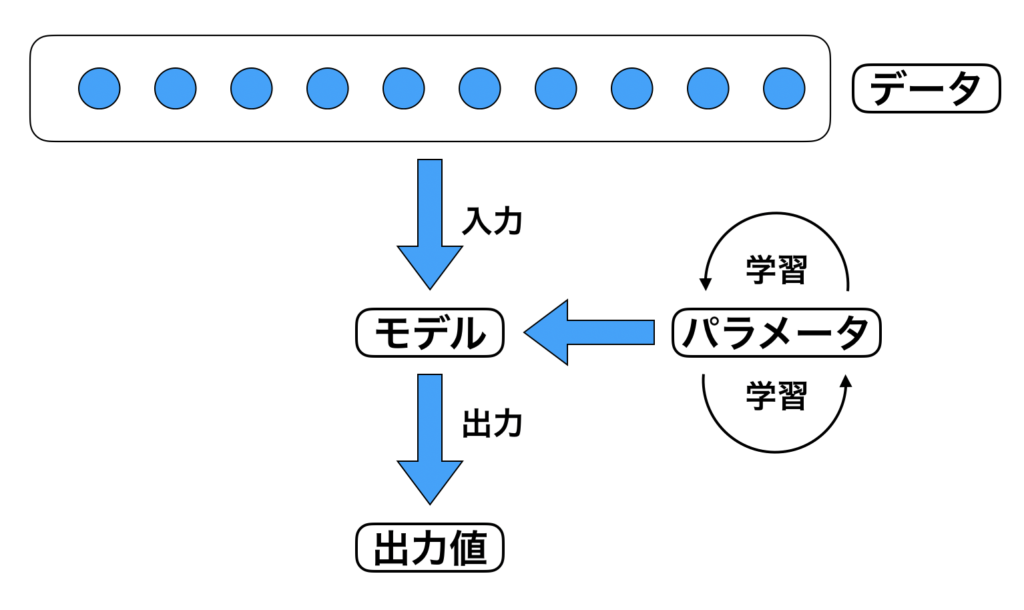
上図の様に、入力されたデータにより予測モデルが作られます。


その予測モデルで重要なポイントは、予測モデルから数値が出力される、という事です。

補足：特徴量について

上図のように、入力したデータは予測モデルを介して出力データに影響力を持っています。


まずこの式を見て下さい。

\(y=f(x)=w \cdot x\)

f は予測モデル、D は入力データになります。
この式の前提としては予測モデルから入力データを求めるために仮定が必要ですが、この式からは x と y は正比例の関係である事が分かります。


出力データに対する入力データの影響力を定量化したものを 特徴量 といいます。


精度の高い予測モデルを作るためには、特徴量の抽出を正確に行う事が非常に重要です。


「特徴量の抽出を行う事が重要」である事を念頭に置いて、予測モデルを作る際の手順を紹介します。[box class="box6"]

1. データ(入力値)を揃える
2. 出力値を元に特徴量を抽出する
3. 予測モデルを選定する
4. モデルを最適化する[/box]基本的にはこの流れに沿って、予測モデルを作成します。

まとめ：機械学習と予測モデル

機械学習と予測モデルの基本的な考え方についてまとめました。


これから予測モデルの作成方法について学んでいきましょう。