実験を行うとき、2つの条件群しか設定しないということは、それほど多くありません。
例えば、新しい降圧薬の効果を調べる場合には、新しい降圧薬を飲む条件と薬を飲まない条件、それからプラセボ条件の3つの条件を設けることもあります。
ここで出てくるのが、3つ以上の条件群の平均値を比較する分散分析になります。
このような3つ以上の条件群の平均値を比較する際に使われるのが分散分析です。
この記事では、1要因の分散分析について詳しく見ていきます。
なお、2要因の分散分析については、この次の記事でお話します。
分散分析の簡単な説明
まず分散分析イメージを簡単に説明してから、具体例を一緒に考えていきましょう。
分散分析について抑えておくべき内容
- 分散分析の概要
- 分散分析の用語の確認
- 分散分析で扱うF値とは
- 分散分析の前提条件
- t検定を繰り返すことと分散分析は異なる【多重性の問題とは】
では早速、見ていきましょう。
分散分析の概要
分散分析を一言でいうと、「3つ以上の条件群の平均値を比較する際に用いられる分析」のことです。
「分散」分析という名前ですが、分散だけで分析するのではなく、平均値も使います。
分散分析のイメージとしては、以下の図を考えると分かりやすいです。
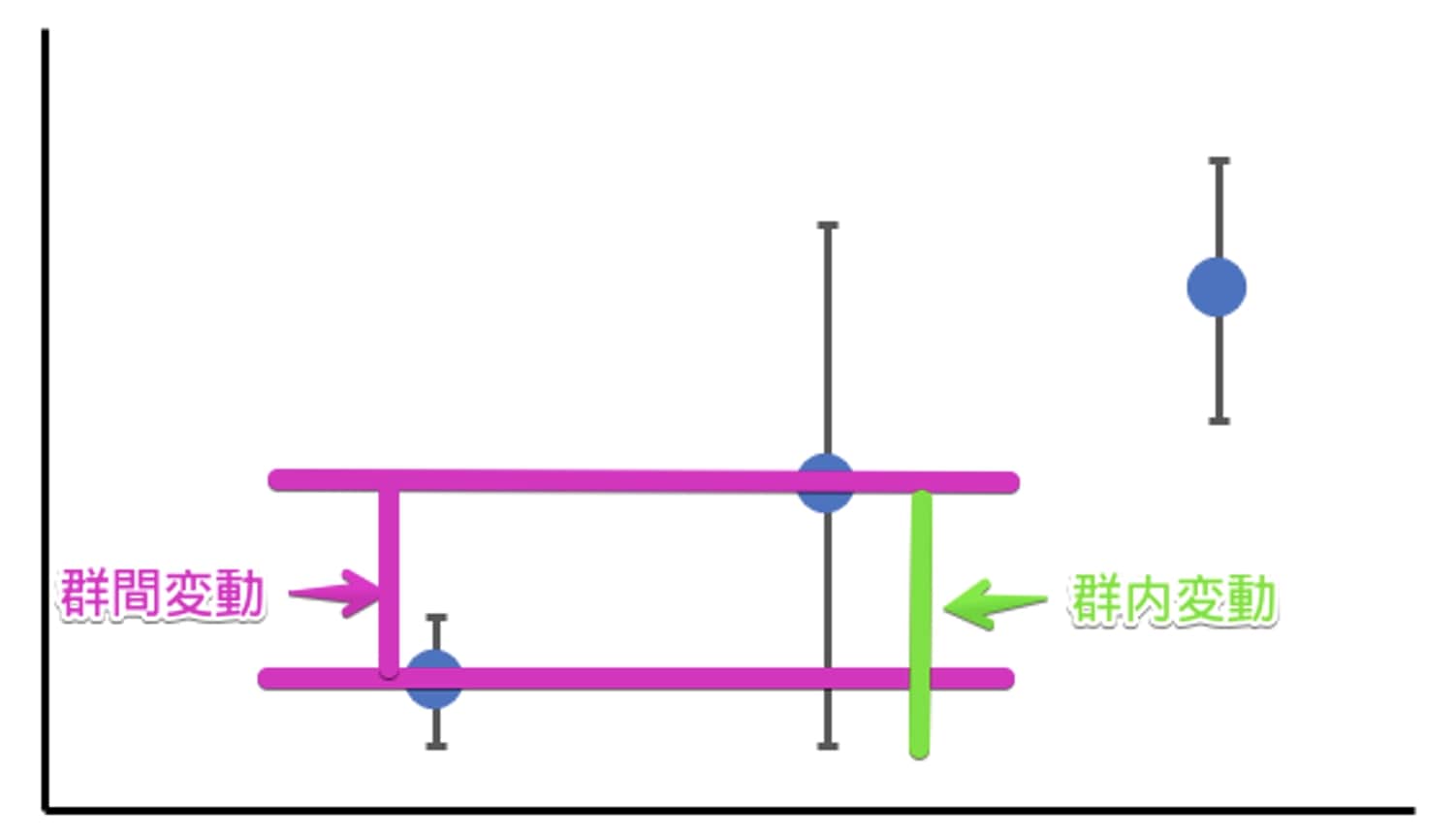
「左の条件と、真ん中の条件の平均値の差」(群間変動)と「真ん中の条件の中での得点のばらつきの差」(群内変動)があります。
群間変動は、「条件群の違い、すなわち独立変数の影響の結果生まれる差」です。
一方で群内変動は、偶然の得点のばらつきで生じる差です。
図の場合、群間変動よりも群間内変動のほうが大きいことが見て取れます。
よって、独立変数は効果を持っていないと判断することができます。
これが分散分析でしている条件群による違いと偶然の誤差による違いのイメージです。
分散分析の用語の確認
分散分析は1要因3水準の分散分析とか2要因の分散分析と呼ばれるものがあります。
この要因は独立変数のことで、水準とは独立変数の中にある条件の数です。
最初に例示した新しい降圧薬の効果を調べる場合、要因は薬の条件となり、3水準は新しい降圧薬、薬なし、プラセボということになります。
なお、「〇元配置の分散分析」と呼ばれることもありますが、この「〇元配置」というのは「〇要因」と同じ意味です。
分散分析で使うF分布とは?
t検定では、t分布のどこにt値があるのかということから統計結果が有意であるのかを判断しました。
分散分析ではF分布というものを用いて、分散分析の結果が有意であるのかを判断します。
F分布は以下のような形をしています。
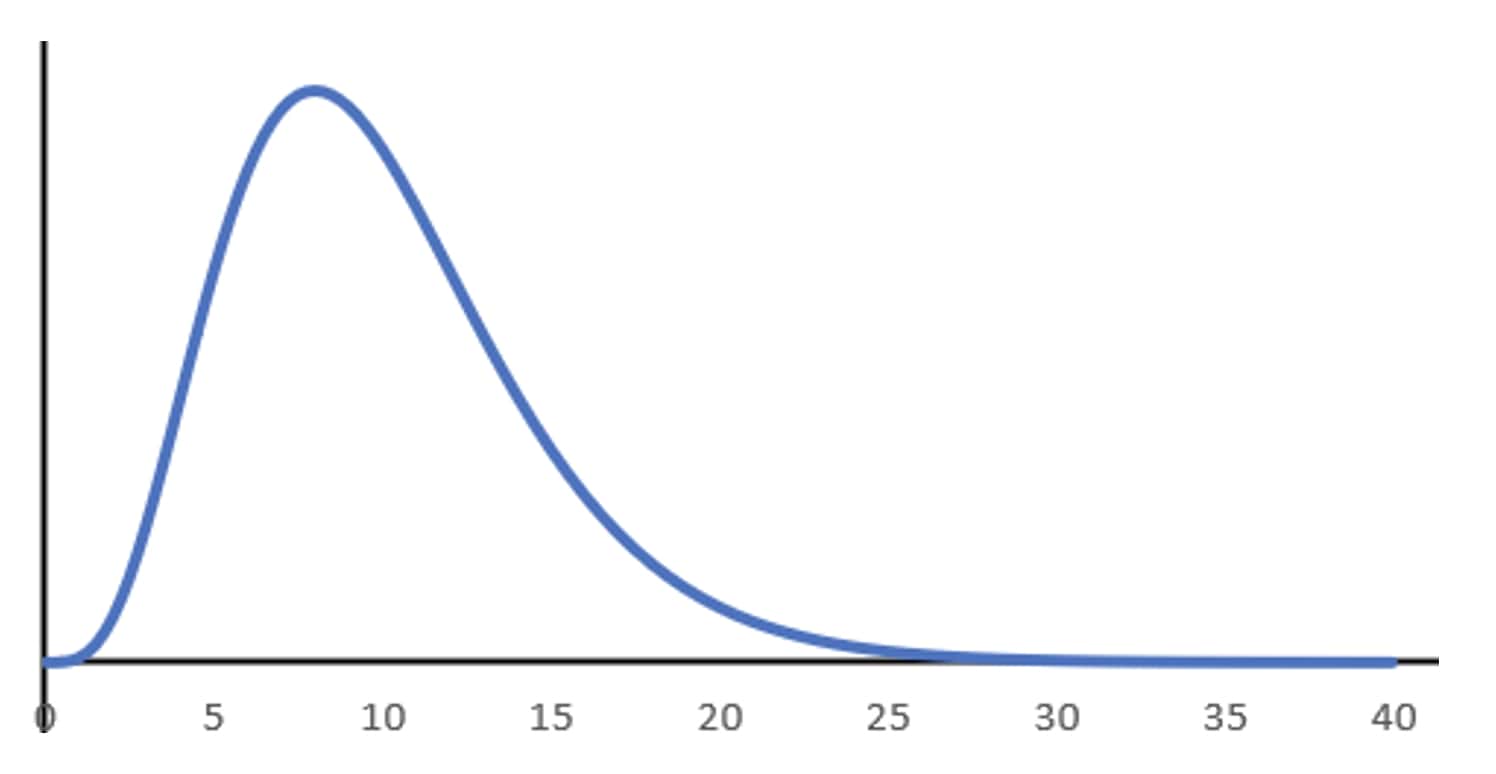
ご覧の通り、t分布とは異なり左右対称ではありません。
また、$x$ 軸のスタートが0になっています。
そのため、対立仮説は「全ての水準のうち、母平均が異なる水準が少なくとも1つある」という片側検定となります。
分散分析の前提条件
分散分析の前提条件はt検定と同じです。
①間隔・比率尺度である量的データであること
②正規分布に従うこと
数値データであれば、多くの場合で分散分析は使えます。
t検定を繰り返すことと分散分析は異なる【多重性の問題とは】
t検定を繰り返せば分散分析と同じことができると思われる人もいるかもしれません。
しかし、両者には違いがあります。
5%水準でそれぞれ分析をしたとしましょう。
分散分析の場合は1回しか分析しないので、そのまま1-0.05=0.95となります。
そのため、本来有意差が出ないデータでも有意差があると判断してしまう確率、すなわち第一種の過誤を犯す確率は1-0.95=5%です。
しかしt検定を3回繰り返す場合、(1-0.05)×(1-0.05)×(1-0.05)≒0.86となります。
そのため、第一種の過誤を犯す確率は1-0.86=14%と、実に3倍近く増えます。
このように、第一種の過誤を犯す確率が高くなるので、t検定を繰り返してはいけないのです。
対応のない分散分析【ストレスレベル高中低、どれが一番パフォーマンスが良いか】
対応のない分散分析について、ストレスレベル高条件・中条件・低条件でのパフォーマンスを比較することによって説明していきます。
なお、対応のない分散分析は、被験者間デザインで取ったデータの分散分析ということもできます。
英語のbetweenをイメージすると分かりやすいと思います。
以下は、ストレスレベル高条件・中条件・低条件における各実験参加者の課題成績です。
| 実験参加者(さん) | 条件 | 成績 |
| A | 高 | 69 |
| B | 高 | 51 |
| C | 高 | 56 |
| D | 高 | 54 |
| E | 高 | 53 |
| F | 中 | 70 |
| G | 中 | 69 |
| H | 中 | 69 |
| I | 中 | 70 |
| J | 中 | 68 |
| K | 低 | 50 |
| L | 低 | 54 |
| M | 低 | 56 |
| N | 低 | 66 |
| O | 低 | 69 |
分散分析で独立変数の影響の有無を調べる
t検定のt値と異なり、分散分析で使うF値には数式のようなものはありません。
以下の手順に従って求めていくことになります。
まず分散分析を行うにあたり、以下の数値を求める必要があります。
| 高条件 | 中条件 | 低条件 | 全体 | ||
| データ数 | 5 | 5 | 5 | 15 | |
| 平均 | 56.60 | 69.20 | 59.00 | 61.60 | |
| 標準偏差 | 7.16 | 0.84 | 8.12 | 8.10 | |
| 分散 | 51.30 | 0.70 | 66.00 | 65.69 | |
| 平方和 | 205.20 | 2.80 | 264.0 | A | ⇦ 全体の平方和 |
| B | ⇦ 誤差の平方和(群内変動) | ||||
| (群内平均 - 全体平均)の和 | 25.00 | 57.76 | 6.76 | ||
| データ数 | 125.00 | 288.80 | 33.80 | C | ⇦ 要因の平方和(群間変動) |
平方和という言葉に聞き覚えがないかもしれません。
れぞれのデータから平均値を引いて2乗したものが偏差ですが、それを全て足したものが平方和です。
つまり、平均値からの各データのばらつきと言えます。
分散分析表とつながるA~Cを埋めていきましょう。
A(全体の平方和)です。
まず各データから全体の平均値を引いたものを2乗していきましょう。
そして、それらを全て足します。
$$(69-61.60)^{2}+(51-61.60)^{2}+\cdots(66-61.60)^{2}+(69-61.60)^{2}=919.60$$
となります。
次にB(誤差の平方和)を求めます。
誤差の平方和は、各条件内でのデータと平均値のズレ合わせたものなので、全ての群の群内変動を合わせたものということになります。
$$205.20+2.80+264.00=472.00$$
となります。
そしてC(要因の平方和)を求めていきます。
要因の平方和は、まず各条件の平均値と全体での平均値のズレを2乗して、それらにデータ数を掛け合わせたものを合計することにより求めることができます。
これは、条件によるズレ(群間変動)ということです。
実際に要因の平方和を求めていきましょう。
$$(56.60-61.60)^{2} \times 5+(69.20-61.60)^{2} \times 5+(59.00-61.60)^{2} \times 5=447.60$$ となります。
ここまで計算できたら、あとは以下の分散分析表を埋めていくだけです。
| 因子 | 平方和 | 自由度 | 平均平方 | F値 |
| 要因 | ① | ④ | ⑦ | ⑨ |
| 残差 | ② | ⑤ | ⑧ | |
| 全体 | ③ | ⑥ | ||
①~③について
- 先ほど計算した通り、埋めていきます。
- ①919.60、②472.00、③447.60となります。
- ※ 残差とは要因以外で説明されるバラツキ、つまり誤差のことです。
④~⑥について
④ 要因の中には高中低3つの条件があるので、3-1=2となります。
⑥ 全体のデータ数は15なので、15-1=14となります。
⑤ ④と⑤を合わせたものが⑥となるので、14-2=12となります。
・⑦・⑧について
平均平方は、各平方和を自由度で割ることによって求まります。
⑦ 919.60÷2=223.80
⑧ 472.00÷12=39.33。
⑨について
- F値は要因の平均平方を残差の平均平方で割ることによって求まります。
- ⑨ 223.80÷39.33=5.69
最後に、条件の効果が統計的に有意か、F分布から調べていきます。
t分布のときは、自由度は1種類だけでしたが、F分布では2種類あります。
1つが要因の自由度で、もうひとつが残差の自由度です。
そのため、F分布表を見るときは1つ目の自由度が2、もう1つの自由度が12のところを見ていきます。
以下のように5%水準での基準は、3.885でした。

今回の統計結果のF値は5.69であり、3.885より大きいので統計的に有意という結果が判断されます。
どこに差があるのかは多重比較で調べる
分散分析で検証できるのは、独立変数の影響があるかどうかであり、どの条件間に差があるかは分かりません。
どの条件間に差があるかは、多重比較という下位検定を行わなければなりません。
多重比較にはHolm法をはじめ色々な方法がありますが、基本的には統計処理ソフトで分析したほうがよいほど計算が複雑です。
また、統計検定2級の分散分析の過去問を見る限り、多重比較までは出題されていないようです(2019年11月時点)。
そのため、分散分析では独立変数の影響があるかどうかを調べることはできるけど、どの条件間に差があるかは分からないということを理解しておけば十分だと思います。
対応のある分散分析~ストレスレベル高中低、どれが一番パフォーマンスが良い?~
対応のある分散分析は、被験者内デザインで取ったデータの分散分析ということもできます。
英語のwithinをイメージすると分かりやすいと思います。
実験参加者に対応があるということなので、各データのばらつきは、条件によるばらつき(群間変動)と偶然の得点のばらつき(群内変動)、さらに個人差のばらつきとなります。
個人差のばらつきというのは、いうなれば実験参加者の特徴によって生まれるばらつきです。
先ほどの対応のない1要因の分散分析で扱ったデータを対応のある1要因の分散分析として分析すると、分散分析表は以下のようになります。
| 因子 | 平方和 | 平均平方 | F値 |
| 要因 | 447.60 | 223.80 | 4.43 |
| 残差(個人差) | 67.60 | 16.90 | |
| 残差(偶然) | 404.40 | 50.55 | |
| 全体 | 919.60 | ||
比べてみると、対応のない1要因の分散分析の残差の部分が、今回の対応のある分析残差(個人差)と残差(偶然)に分かれていることが分かります。
また、全体のデータのばらつきに個人差によるばらつきも加えて考慮しているので、F値が少し小さくなっていることが分かります。
2019年11月までの統計検定2級の過去問を見る限り、対応のある1要因の分散分析は出題されたことはないようです。
おそらく、計算過程が複雑になるからでしょう。
そのため、対応のない1要因の分散分析の考え方をしっかり押さえておくことが大切です。
今回は以上となります。
