この記事では分散分析を理解して頂いてから、練習として解くための練習問題となります。
-

2要因の分散分析(二元配置分散分析)について
続きを見る
上記の記事と以下の動画を視聴した上で、分散分析についての理解を深めていきましょう。
それでは理解がまとまったところで、問題に移りましょう。
① 分散分析の基礎知識
【問題】以下の3つの文章について正誤判断してください。
- 分散分析では、全体のデータの散らばりは、条件による散らばりと偶然誤差による散らばりの和からなる。
- 分散分析における対立仮説は「全ての条件群の母平均は異なっている」である。
- 分散分析で帰無仮説が棄却された場合、どこの条件間で母平均に有意な差があるか分かる。
【解答・解説】
- 〇 全体の平方和=条件群の平方和+誤差の平方和となります。
なお平方和とは、データから平均値を引いて2乗したもの(偏差)を全て足したもののことです。
平たく言えば、データの散らばりのことです。 - × 分散分析の帰無仮説は「全ての条件群の母平均は等しい」です。
これを否定するには、全ての条件群で母平均が違っていなくてよく、1つの条件群で母平均が違えば帰無仮説は否定されます。
よって、対立仮説は「少なくとも1つの条件群で母平均が異なっている」となります。 - × 3つの条件があるとして、以下のいずれの場合でも分散分析の結果は同じように有意となります。
A条件の母平均 ≠ B条件の母平均≠C条件の母平均
A条件の母平均 = B条件の母平均≠C条件の母平均
A条件の母平均 = C条件の母平均≠B条件の母平均
B条件の母平均 = C条件の母平均≠A条件の母平均
そのため、分散分析で分かることは条件群の影響があることに過ぎず、どの条件群で差があるのかは分かりません。どの条件群で差があるかを調べるためには、下位検定の多重比較を行わなければなりません。
このように分散分析の考え方ができるかという問題は2017年6月や11月に出題されています。
分散分析の帰無仮説や対立仮説の考え方、そこから導き出される結論は、分散分析が出題されるときによく尋ねられる問題です。分散分析の考え方の基礎をしっかり押さえておきましょう。
② 分散分析の実践
以下は、2016年~2020年のハワイのホノルルの各月の平均気温のデータです。
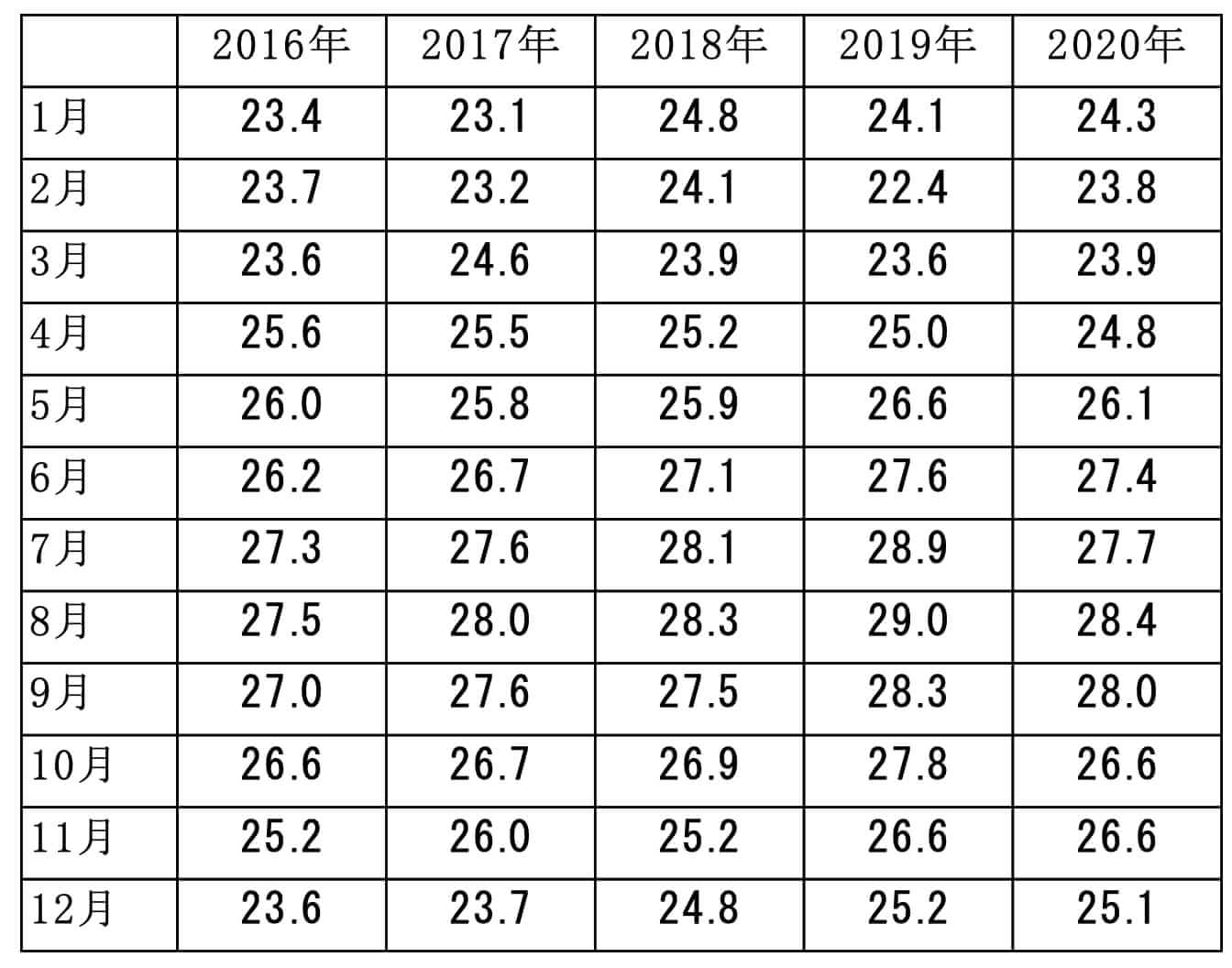
資料:気象庁 世界の天候データツール
このデータを用いて月を変動要因とする一元配置分散分析を行った結果,次の表を得ました。
【問題】
① j 年 i 月の気温を、
$\mathrm{y}_{\mathrm{ij}}(\mathrm{i}:=\cdot 1, \cdots, 12 ; \mathrm{j}=2016, \cdots, 2020)$とし,
月ごとの平均を $\bar{y}_{i}$、年ごとの平均を$\bar{y}_{\mathrm{j}}$,全体の平均を $\bar{y}$ とした場合、
水準間平方和($\mathrm{S}_{\mathrm{A}}$)と残差平方和($\text { Se }$)の式を表してください。
② 表のaとbの値はそれぞれ何になりますか。
③ 分散分析の結果、どのようなことが言えますか。
【解答・解説】
→①水準間平方和($\mathrm{S}_{\mathrm{A}}$)は要因の平方和(群間変動)のことなのです。
まず各条件の平均値と全体での平均値のズレを2乗して、それらにデータ数を掛け合わせたものを合計することにより求めることができます。
そのため、水準間平方和($\mathrm{S}_{\mathrm{A}}$)は以下の式によって求まります。
$S_{A}=\sum_{i=1}^{12} 5\left(\bar{y}_{i} \cdot-\bar{y}_{. .}\right)^{2}$
$\left(\bar{y}_{i .}-\bar{y}_{. .}\right)^{2}$ の部分が、「各条件の平均値と全体での平均値のズレを2乗」している部分です。
そこにデータ数「5」年分を掛け、$\sum$で1月~12月を加算するとことで式が完成します。
残差平方和($\text { Se }$)は誤差の平方和(群内変動)は、各条件内でのデータと平均値のズレの2乗を合わせたものです。
そのため、残差平方和($\text { Se }$)以下の式によって求まります
$S_{e}=\sum_{i=1}^{12} \sum_{j=2016}^{2020}\left(\bar{y}_{i j}-\bar{y}_{i} .\right)^{2}$
$\left(\bar{y}_{i j}-\bar{y}_{i} .\right)^{2}$ の部分が、各条件内でのデータと平均値のズレの2乗を合わせたものです。
$$\sum_{j=2016}^{2020}$$
の部分で、それぞれの月のデータを加算していくことになります。そして
$$\sum_{i=1}^{12}$$
で1月~12月を加算するとことで式が完成します。
②「水準間」の自由度は、水準の数から1を引くことで求まります。12-1=11が答えです。
「残差」の自由度は「全体」の自由度から「水準間」の自由度を引くことで求まります。
「全体」の自由度は、全てのデータの数から1を引いたものなので「(12×5)-1=59」です。
よって、「残差」の自由度は「59-11=48」となります。
③ 問題文よりF値は44.1です。以下は5%水準でのF分布表です。

今回のF(11,48)=44.1は、自由度が12と48のF値2.579より大きいので、p値は5%より小さく、5%水準で有意であることが分かります。
一元配置分散分析の帰無仮説は「全ての水準で母平均が等しい」であり、対立仮説は「少なくとも1つの水準の母平均が異なる」です。
帰無仮説が棄却され、対立仮説が採用されるため、少なくとも1つの水準の母平均が異なると言えます。
ハワイは年間を通して温度差が小さいとは言われますが、それでも実際に分析してみると、月の違いが気温に及ぼす影響があることが分かります。
これと同じような問題が2019年11月にも出題されています。分散分析の計算過程は大変だからか計算自体はさせないようですが、どんな式で平方和や自由度を算出するのかを理解しておく必要があります。
