この記事では回帰分析の基本を理解して頂いてから、知識を確認するための練習問題(統計検定2級レベル)となります。
まずは以下の記事を読んで見て下さい。
-

回帰分析について
続きを見る
それでは理解がまとまったところで、問題に移りましょう。
① 単回帰分析の確認
【前提】
各都道府県の直近1週間の人口10万人あたりの、ある感染症の感染者数と2回目のワクチン接種率のデータを用いて、次の単回帰モデルを推定しました。
直近1週間の人口10万人あたりの$ 感染者数 = a+b×2回目のワクチン接種率+ u(誤差)$
とします。
なお、$u$(誤差)は互いに独立に正規分布に従うものとします。
資料
- 直近1週間の人口10万人あたりの感染者数(2021/7/30迄の情報より算出)
2回目のワクチン接種率に対応する変数 vaccination を作成し、統計ソフトウェアを利用して直近1週間の人口10万人あたりの感染者数について以下の単回帰モデルを推定したところ、次の出力結果を得ました。なお、出力結果の一部を削除しています。
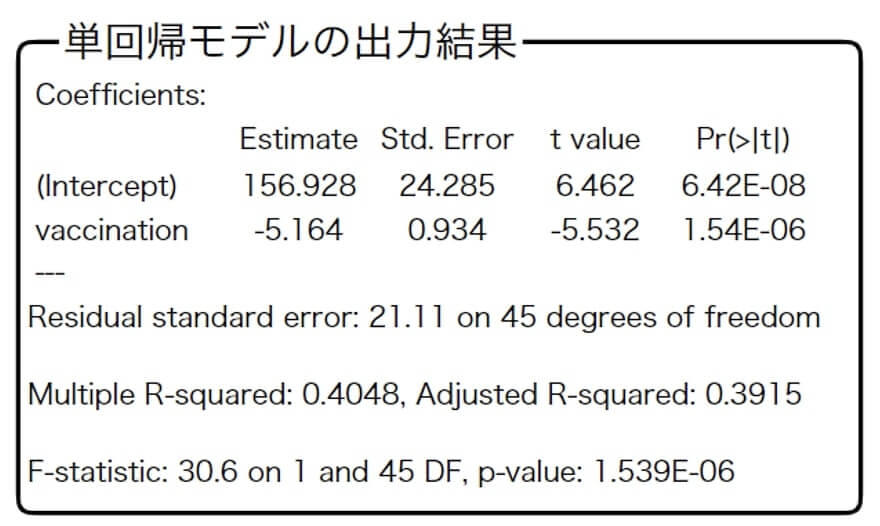
上記の前提を踏まえて、以下の問題を解いてください。
【問題】正しい記述を選んでください。
- 目的変数を「直近1週間の人口10万人あたりの感染者数」ではなく「直近1週間の人口100万人あたりの感染者数」とした場合、回帰係数もt値も1/10になる。
- vaccinationの回帰係数について、両側検定でも片側検定でもP値は1.54E-06で同じである。
- 予測値の平均値が23.7であるので、元のデータy の平均値も23.7である。
- 自由度調整済み決定係数は、重回帰モデルにおいて説明変数の数に応じて決定係数を調整したものである。
そのため、説明変数が1つである単回帰モデルでは決定係数と自由度調整済み決定係数は等しくなる。
今回の推定結果では単回帰モデルの決定係数は0.4048、自由度調整済み決定係数は0.3915と異なっているが、これは計算の丸め誤差のためである。
【解答・解説】c
- ×
標準化偏回帰係数と異なり、回帰係数も偏回帰係数も元のデータの単位に依存します。そのため、目的変数が1/10となれば回帰係数も1/10となります。しかし、t値は変わりません。 - ×
両側検定の場合と片側検定の場合では、算出されるp値は異なります。
なお回帰係数のt検定では、「回帰係数は0である」という帰無仮説に対する検定が行われます。
「回帰係数が 0 より大きい」あるいは「回帰係数が 0 より小さい」ではないため、両側検定となるのです。回帰係数のt検定が有意であるということは、目的変数に対する説明変数の影響力が統計的に見て意味があることを表しています。 - ◯
一つひとつの予測値と元のデータとの間にはプラス方向あるいはマイナス方向のズレ(残差)があります。しかし、残差全てを合計すると0になるため、予測値の平均と元のデータの平均は必ず等しい値になります。
なお残差の特徴は過去問でよく出題されているため、全ての予測値 $y ̂$ に残差を加えると元のデータ $y$ となることも併せて覚えておきましょう。 - ×
自由度調整済み決定係数とは、自由度を調整することで(具体的にはサンプルサイズ-説明変数の数 $-1$ )決定係数の調整を行ったものです。
ただ、この説明では結局のところ単回帰分析の決定係数と自由度調整済み決定係数の違いがよく分からないと思います。
重回帰分析では説明変数の数が違うため自由度そのものも変わるので分かりやすいですが、単回帰分析でも両者は文脈が異なります。例えば、大学生100人を対象にしたアンケート調査を例に考えて見ましょう。研究で明らかになったことは、母集団である日本人の若者に当てはまる傾向として解釈したいと思います。しかし、この調査で推定された回帰式は「今回の調査で対象となった100人」のデータに対する予測となるものです。
理論上の「無作為に選ばれた日本人の若者100人」のデータとはどうしても誤差やズレがあるため、調査データで推定された回帰式では予測精度は悪くなります。そこで「無作為に選ばれた日本人の若者100人」に対する予測ができるように決定係数の値を修正したものが「自由度調整済み決定係数」となります。
② 重回帰分析の確認
【前提】
直近1週間の人口10万人あたりの感染者数が2回目のワクチン接種率と人口密度、喫煙率で説明できるかどうかを検証するため、次の重回帰モデルを推定しました。
直近1週間の人口10万人あたりの感染者数
$ =a+b1×2回目のワクチン接種率+b2×人口密度+b3×喫煙率+ u(誤差)$
なお、$u$(誤差)は互いに独立に正規分布に従うものとします。
資料
2回目のワクチン接種率に対応する変数をvaccination、人口密度に対応する変数をPD、喫煙率に対応する変数をsmokeとして、以下の重回帰モデルを推定したところ、次の出力結果を得ました。なお、出力結果の一部を削除しています。
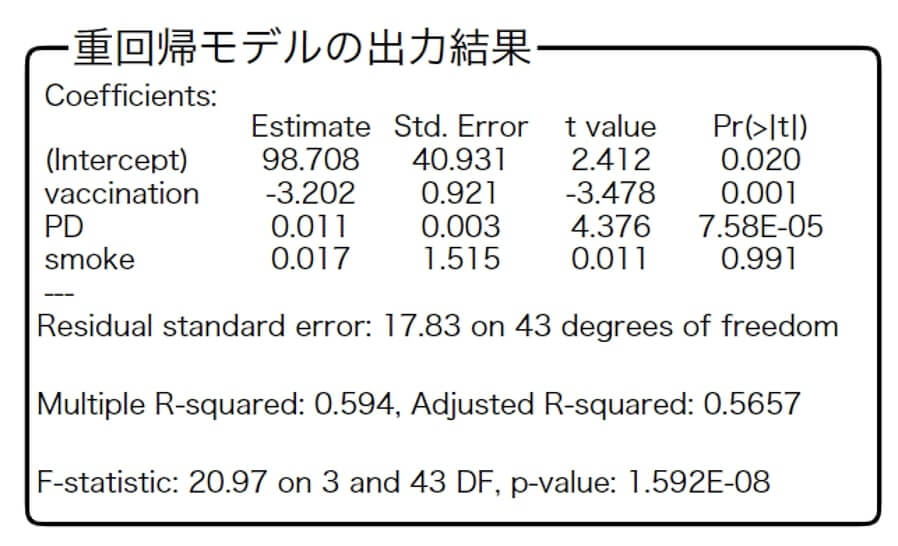
【問題】
- 2回目のワクチン接種率が1%高くなると、直近1週間の人口10万人あたりの感染者数は3.202人少なくなる傾向にある。
- 人口密度の偏回帰係数は0.011と非常に小さい値であるため、人口密度から直近1週間の人口10万人あたりの感染者数への影響はほぼないものと言える。
- ワクチン接種率と人口密度が一定の場合、「喫煙率が1%大きくなると直近1週間の人口10万人あたりの感染者数は0.017人多くなる」と解釈される。
- ワクチン接種率が25.9、人口密度が305.2、喫煙率が19.7のとき、直近1週間の人口10万人あたりの感染者数の予測値は約16人である。
【解答・解説】
- ◯
- ×
説明変数から目的変数への影響が有意かどうかは、偏回帰係数のp値から判断されます。
一般的にp値が0.05よりも小さければ、その説明変数から目的変数への影響は意味があるものと言えます。
今回 $p$ 値は $7.58E-05$ であるため、 $p=0.0000758$ であり、説明変数から目的変数への影響は有意です。
なお、偏回帰係数の大きさは元々のデータの単位に依存したものです。説明変数や目的変数を標準化した標準偏回帰係数を求めたところ、ワクチン接種率では-0.395であるのに対して人口密度では0.498となりました。そのため、あくまでも今回用いた時点でのデータに限定すれば、ワクチン接種率よりも人口密度のほうがより強い影響を及ぼしていると言えます。 - ×
喫煙率の偏回帰係数のp値は0.991であるため、喫煙率については「回帰係数は0ではない」という帰無仮説は棄却されません。つまり、喫煙率については「回帰係数は0である」と解釈されます。 - ◯
出力結果の回帰係数を重回帰モデルに当てはめていくと、以下の式になります。
直近1週間の人口10万人あたりの感染者数
=98.708-3.202×2回目のワクチン接種率+0.011×人口密度+0×喫煙率+ u(誤差)
この式にワクチン接種率=25.9、人口密度=305.2、喫煙率=19.7を代入したところ、直近1週間の人口10万人あたりの感染者数の予測値は15.78となりました。よって、正しいと判断されます。
③ 単回帰分析と重回帰分析の結果の比較
次の記述は①で推定した単回帰モデルと、②で推定した重回帰モデルの比較に関するものです。
【問題】
- 重回帰モデルにおいて仮にワクチン接種率と人口密度、喫煙率の係数が等しいとすると、単回帰モデルになる。
- 同じワクチン接種率の傾きなので、単回帰モデルでも重回帰モデルでもワクチン接種率の回帰係数は理論上は同じ値になる。
しかし、実際には単回帰モデルでは-5.164、重回帰モデルでは-3.202と全く違う値になっている。この原因として多重共線性が考えられる。 - 単回帰モデルでは、ワクチン接種率と直近1週間の人口10万人あたりの感染者数との関係しか分析できない。
しかし重回帰モデルでは、ワクチン接種率と直近1週間の人口10万人あたりの感染者数との関係と、人口密度と直近1週間の人口10万人あたりの感染者数との関係、喫煙率と直近1週間の人口10万人あたりの感染者数との関係を分けて分析できる。 - 重回帰モデルのほうが単回帰モデルよりも決定係数は高かった。よって、重回帰モデルのほうを選択すべきである。
【解答・解説】
- ◯
重回帰モデルの全ての偏回帰係数が等しいとすると、結局のところ1つの偏回帰係数で回帰式を表すことができます。そのため、単回帰モデルと言えます。 - ×
重回帰分析では偏回帰係数が求められます。偏回帰係数は他の変数の影響を統計的に取り除いたときの当該変数の影響力であるため、同じ説明変数であっても回帰係数と偏回帰係数の値は異なるのです。
なお、多重共線性とは相関の強い説明変数同士を1つの重回帰モデルに投入してしまうことで正しい分析ができなくなることです。
今回の重回帰モデルの説明変数であるワクチン接種率と人口密度、喫煙率で相関分析を行ったところ、ワクチン接種率と人口密度でのみ-0.49と中程度の負の相関が認められました。
多重共線性の問題があるかはVIFという数値を求めることで確認できますが、VIFは1.061~1.371となりました。
一般的にVIFが10以下であれば多重共線性の問題はないとみなされること、VIFの理想値は2以下であることを考慮すると、今回は多重共線性の問題は生じていないと判断できます。 - ◯
- ×
重回帰モデルと単回帰モデルでは説明変数の数が違います。
そのため、どちらのモデルのほうが良いか判断するには、自由度調整済み決定係数が使われます。
まとめ
回帰分析はRやPythonを使えば簡単に計算が出来ますが、統計検定2級レベルであれば、知識・結果の解釈を問われることがほとんどです。(私は個人的に統計ソフトよりもRを好んでいますが、今回の記事はSPSSを使用していますし、統計ソフトを使用してももちろん構いません。)
補足
- $t$ 値:傾きの推定値(偏回帰係数)/ 標準誤差
- Std.Error :標準誤差
- 回帰係数の自由度:$n$(サンプルサイズ)$-k$(説明変数の数)&-1$
- 予測値
単回帰分析・重回帰分析の理解のお役に立てましたら幸いです。
