調査や実験を行うとき、独立変数が2要因以上になることもあります。
この際に重要となってくるのが、「実験計画と、2つの条件群の平均値を比較する分散分析(2要因の(二元配置)分散分析)」です。
独立変数が2要因、3要因の場合は、1要因だけの場合と異なり、相乗効果のように要因が組み合わさることで見られる影響も出てきます。
また、1要因のときは各水準を無作為の順序で実験すればよかったですが、2要因以上になると、実験を行う順序もしっかり考えなければなりません。
なお、1元配置の分散分析の方法については、以下の記事を参照にしてください。
ここで、少しこんがらがってしまっている方は以下の動画が非常に分かりやすいので整理してみてください。
少し理解が深まったでしょうか。
本記事では、実験を行う前に考えるべき実験計画について説明してから、2要因の分散分析について詳しく見ていきます。
実験計画【要因が複数の場合、変数の関係性を明確にする】
実験計画とは、研究目的を元に効果的な条件・群の組み合わせを考えて実施したり、最適な統計手法で分析したりすることです。
ランダムに条件群を組み合わせて実験を行えば大丈夫だという甘い考えで実験を行うと、信頼できるデータを得られません。
また、ある組み合わせのデータが足りず、実験データを追加で取らなくてはならなくなったりする恐れもあります。
条件群の組み合わせを考えることは、信頼できるデータを効率的に収集できることにつながりますので、学んでおいて損はありません。
実験計画の考え方で最も有名なものに、フィッシャーの3原則があります。
フィッシャーの3原則
フィッシャーの3原則は、以下の3つからなります。
反復
「反復」とは、各条件について少なくとも2回、可能ならば3回以上繰り返してデータを取るべきであるということです。
1回だけしかデータを取っていなければ、そのデータが条件の効果で起こったものなのか、それとも偶然なのか分からないためです。
また繰り返す数が2つだと、2つのデータの値に大きな差が出てしまった場合、片方を外れ値とみなしてよいのか、それとも元々そのぐらいのばらつきがあってもおかしくないのか判断できません。
でも、少なくとも3つぐらいデータがあれば、外れ値なのかバラツキなのか判断できます(もちろん、さらに多く繰り返したほうが、外れ値かどうか判断しやすくなります)。
例えば、条件がAからCの3つあって、1日5回の実験を行うとすると、それぞれの条件を5回ずつ繰り返して行うことが反復にあたります。
| 1日目 | 2日目 | 3日目 | |
| 条件 | ABCBC | BACCA | CBABA |
お気づきの方もいると思いますが、これは良い実験手順とは言えません。
それというのも、実験者は実験を繰り返すほど実験手順が上達するためです。
患者さんに薬を投与するだけの簡単な実験手続きであったとしても、実験者の実験慣れ・上達といった他の要因が結果に影響を及ぼすのは避けたいものです。
そこで、次の「無作為化」が大切になります。
無作為化
「無作為化」とは、実験条件を無作為の順序で繰り返すということです。
先ほどのA~C条件の実験に無作為化の要素を加えると、実験を行う順番は以下にようになります。
順番の無作為化を行う方法としては、地道に頭で色々なパターンを考えるのもひとつの手段ですが、サイコロを振って順番を決めることや、エクセルの乱数機能で順番を決めることもあります。
とはいえ、同じ時間帯に毎回実験が行えればよいのですが、1日目は午前中に全ての実験を行い、2日目は午後に全ての実験を行う、3日目は午前に2回、午後に3回実験を行うということをしていては、上手な実験ができているとは言えません。
それというのも、フィッシャーが行った肥料の効果を調べるための実験のように、実験の内容によっては実験を行う時間帯や場所(系統誤差)などの影響を受けることがあるからです。
そこで大切になるのが「局所管理」という考えです。
局所管理(ブロック化)
「局所管理」では、例えば時間帯によって影響を受ける場合は、午前の実験と午後の実験のように均等にしたブロックを作って、午前と午後のどちらのブロックでもA~C条件が均等に行われるようにします。
そうすると、無作為化よりもさらに系統誤差の影響を少なくすることができます。
| 1日目 | 2日目 | 3日目 | |
| 午前の実験 | ABC | BAC | CBA |
| 午後の実験 | BC | CA | BA |
乱塊法
フィッシャーの3原則の反復と無作為化、局所管理の全てを考慮した実験デザインのことは、「乱塊法」と呼ばれます。
乱塊法で実験を行うことができれば、正しくデータを取れていると言えるでしょう。
なお精度の高い機械を使う実験や、1人の実験者だけで短時間に全ての条件を試験できる実験のように、時間帯や場所などの影響を受けないこともあります。
そういった場合は、反復と無作為化だけを組み合わせた「完全無作為化法」で十分です。
分割法
フィッシャーの3原則で指摘される通り、実験順序を無作為にすることは非常に重要なことです。
しかし、時間や費用の面から、完全に無作為な順序で実験を行うことができないこともあります。
そのような場合、分割法と呼ばれる実験方法が行われます。
A要因(少ない・中程度・多い)とB要因(肥料a・肥料b・肥料c・肥料d)があったとしましょう。
まず、A要因をどの順序で行うかを無作為に決めます。
そして、A要因を固定したまま、B要因を無作為な順序で変えて実験を行っていきます。
具体的には、以下の通りに実験が行われます。
- A要因(多い)×B要因(肥料a・肥料b・肥料c・肥料d)の組み合わせで一通り実験を行う
- A要因(中程度)×B要因(肥料a・肥料b・肥料c・肥料d)の組み合わせで一通り実験を行う
- A要因(少ない)×B要因(肥料a・肥料b・肥料c・肥料d)の組み合わせで一通り実験を行う
要因の分散分析
2要因の分散分析とは、独立変数が2種類になった分散分析のことです。
「データ全体の平均値からそれぞれの条件の水準の平均値がどれほどズレているか」というポイントは、1要因の分散分析と同じです。
要因の分散分析との違い(主効果と交互作用)
2要因の分散分析と1要因の分散分析との大きな違いは、独立変数の効果(主効果と呼ばれます)だけではなく、独立変数が組み合わさることで生まれる相乗効果(交互作用と呼ばれます)を調べることができる点です。
学年と授業法の違いが授業へのやる気に及ぼす影響(架空データ)を使って、交互作用について考えていきましょう。
交互作用には、以下の3パターンがあります。
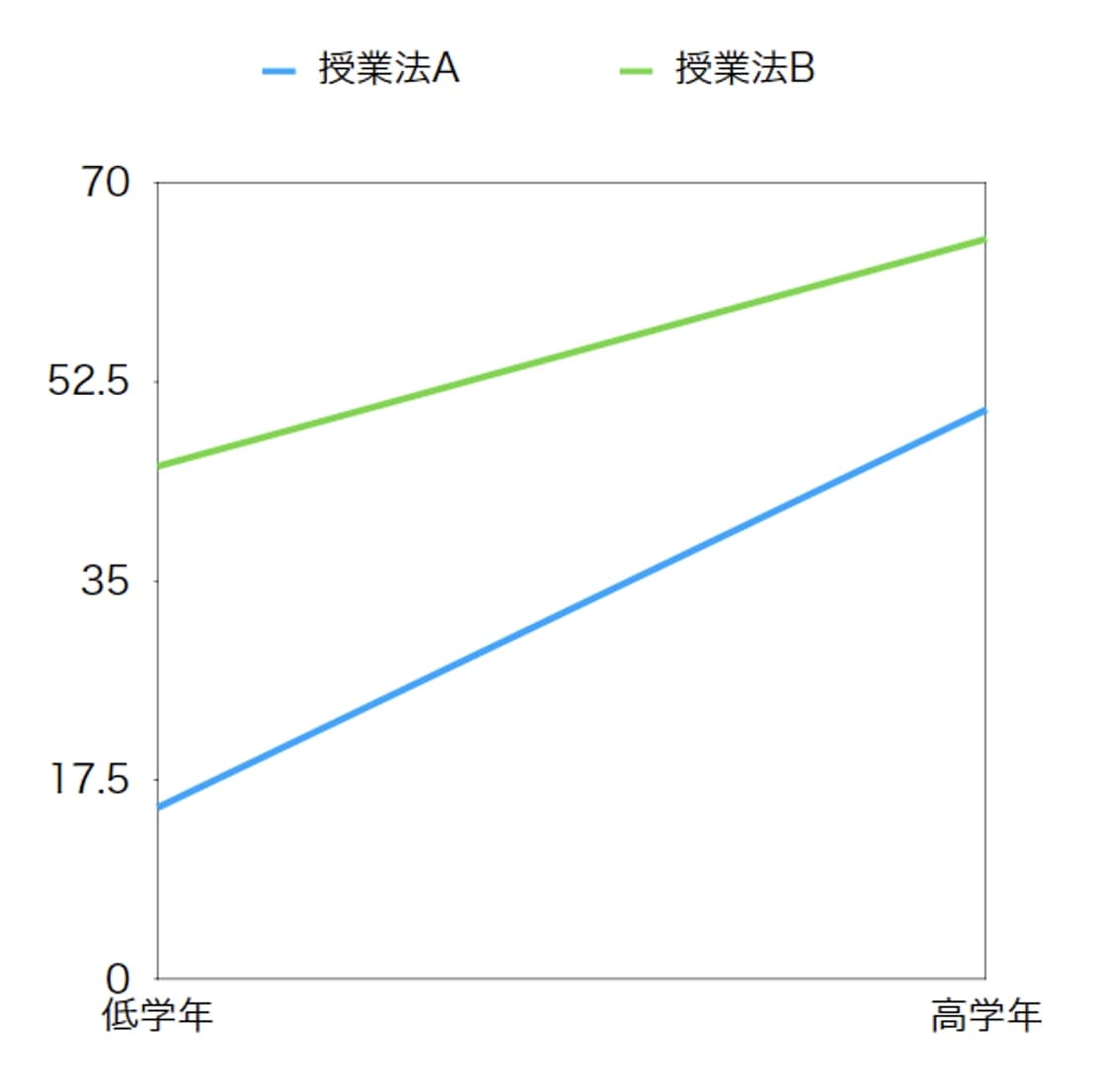 このグラフでは、授業法Aのほうが授業法Bよりもやる気を高めるという授業法の主効果があることや、高学年のほうが低学年よりもやる気が高いという学年の主効果が分かります。
このグラフでは、授業法Aのほうが授業法Bよりもやる気を高めるという授業法の主効果があることや、高学年のほうが低学年よりもやる気が高いという学年の主効果が分かります。
ただし、高学年では低学年と比べ、授業法AとBによるやる気の得点の差が小さくなっていますよね。
このように、学年が高いと授業法の効果が小さくなるというように、独立変数が組み合わさることで効果が変わってくるのが交互作用です。
今回は独立変数が組み合わさることで小さくなりましたが、条件が組み合わさることで大きくなるタイプの交互作用、いわゆる相乗効果となることもあります。
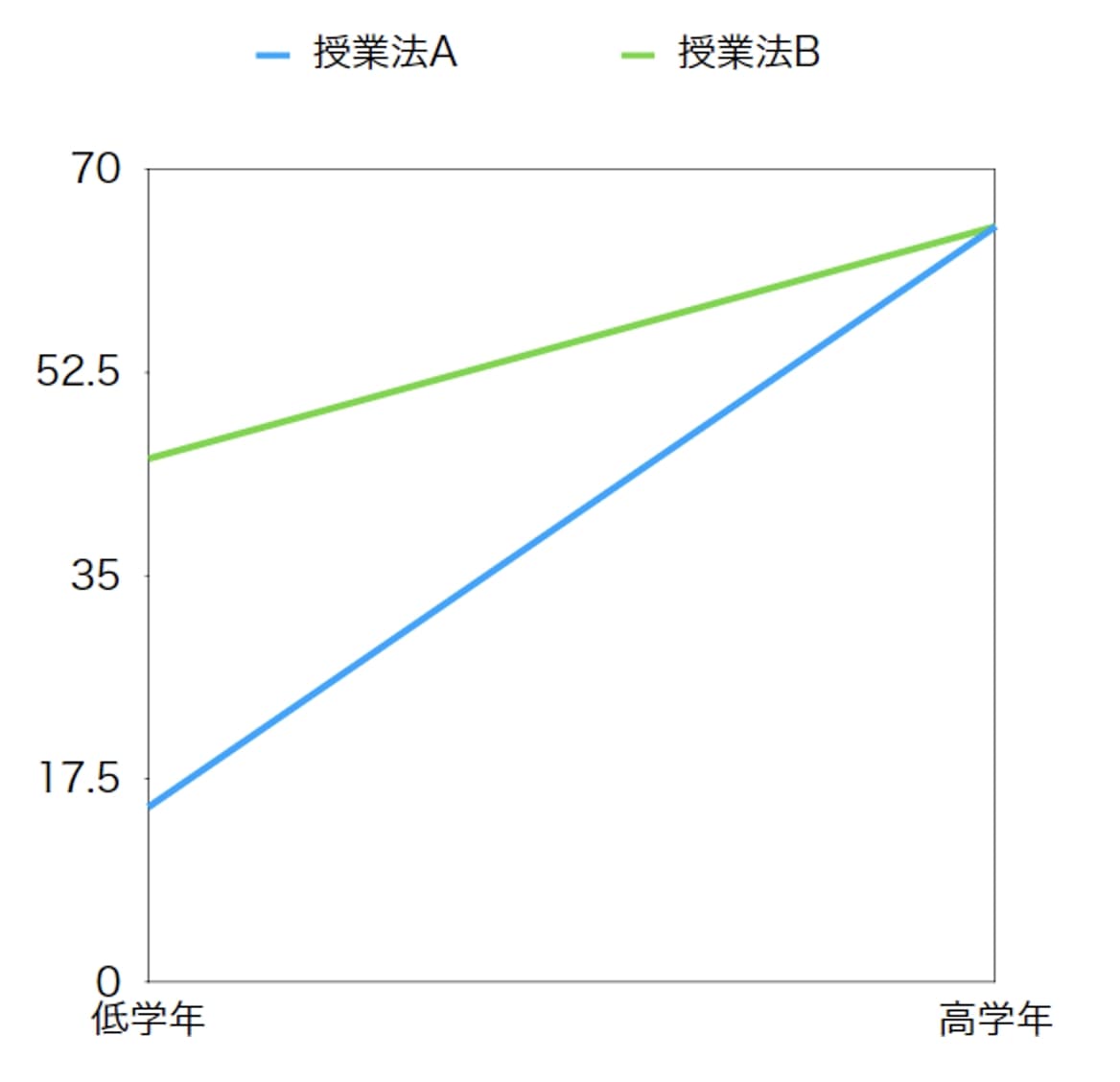
このグラフでは、授業法の主効果や学年の主効果はあります。
しかし、低学年では授業法AとBでやる気の得点に差がある一方で、高学年では授業法AとBでやる気の得点に差がありません。
このことから、授業法の効果は低学年ではあるけれども高学年ではないことが分かります。
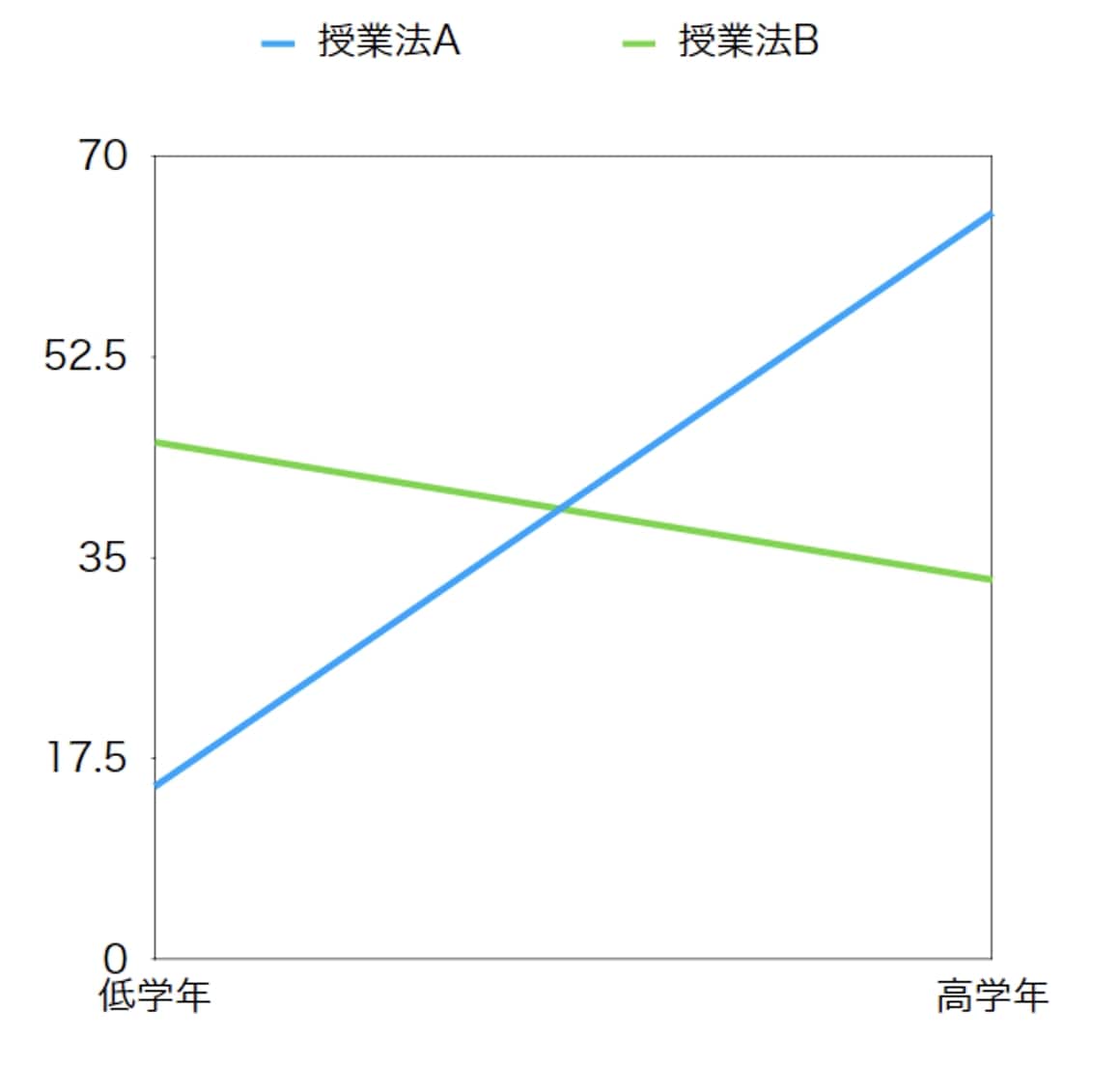
今度は、交差しているタイプのグラフです。
低学年では授業Bのほうがやる気を高めるのに有効である一方、高学年では授業法Aのほうがやる気を高めるのが有効であることが分かります。
このようなタイプの交互作用となることで、一方の独立変数の性質によってもう一方の独立変数の影響の方向性が変わります。
3つの計画(被験者間計画、被験者内計画、混合計画)
t検定や1要因の分散分析で対応のない(被験者間計画)、対応のある(被験者内計画)という言葉が出てきました。
2要因の分散分析でも、これは出てきます。
2つの独立変数共に実験参加者が対応していない場合を被験者間計画、2つの独立変数共に実験参加者が対応している場合を被験者内計画と呼びます。
1つの独立変数は対応ありだけど、もう1つの独立変数については対応なしの場合は、混合計画と呼ばれます。
2要因の分散分析を実際に計算してみよう(被験者間計画)
では、実際に2要因の分散分析を行ってみましょう。
一番考えやすいことから、ここでは被験者間計画の研究例で考えていきます。
興味深い結果の研究がありましたので、ご紹介します。
内面的魅力と身体的魅力が異性への好意にどのような影響を及ぼすかについての研究です。
※大まかな分析結果は参考にしていますが、平均値や平方和などの実際の分析データは架空のものです。そのため、分析結果には多少の食い違いがあります。
元の研究では内面的魅力と身体的魅力、さらに性別の3要因の分散分析を行っていますが、ここでは2要因の分析を考えるため、女性において外見的魅力と内面的魅力が異性への行為に及ぼす影響を見ていきます。
以下は、女性における各条件の距離のグラフです。
※ 距離が小さいほど、好意が高いことになります。
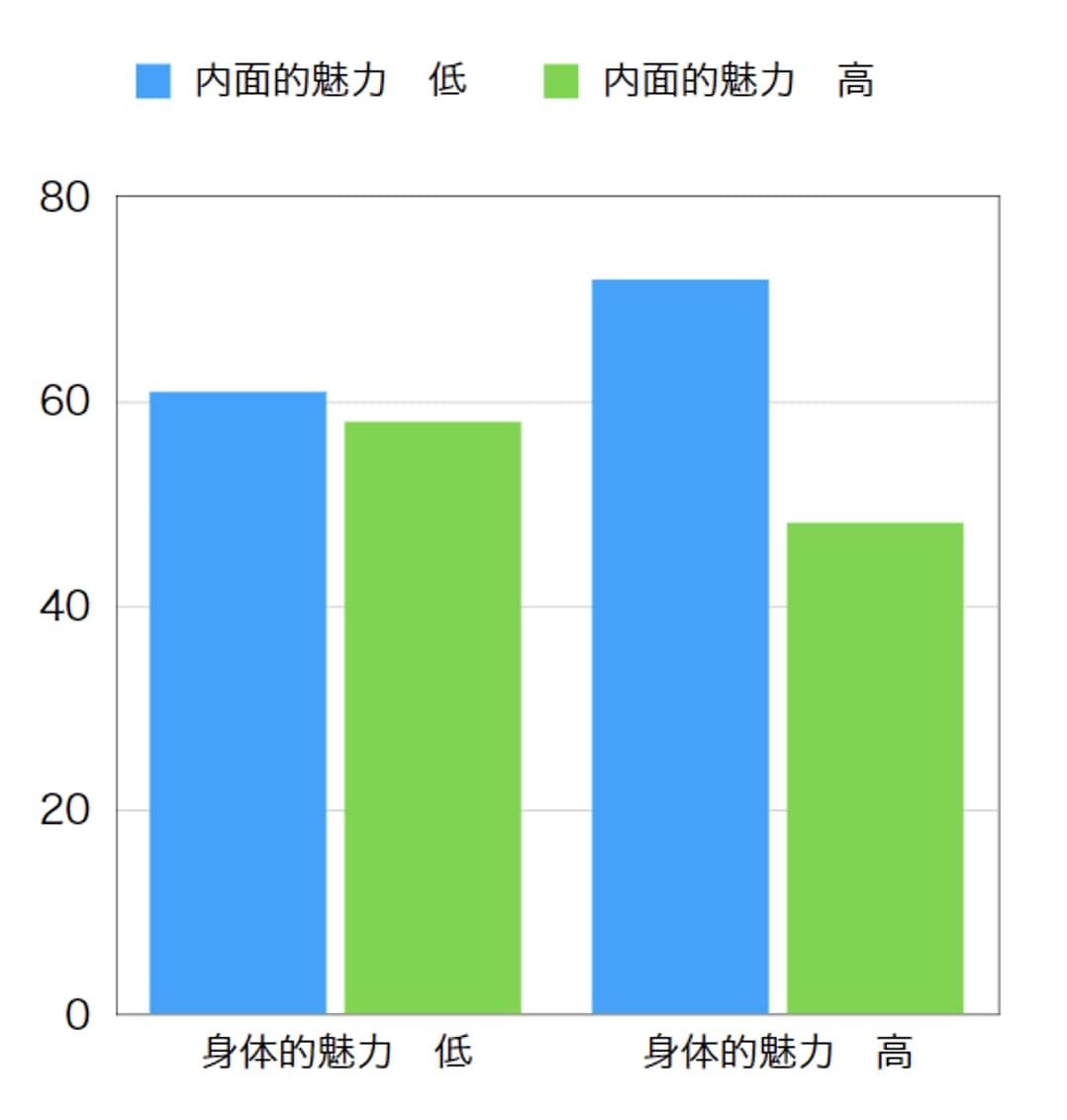
仮に、実験データが以下のようになったとします。
| 身体的魅力 低 | 身体的魅力 高 | |
| 内面的魅力 低 | 61 | 72 |
| 42 | 80 | |
| 69 | 84 | |
| 70 | 64 | |
| 63 | 60 | |
| 内面的魅力 高 | 58 | 48 |
| 65 | 32 | |
| 49 | 56 | |
| 70 | 45 | |
| 48 | 59 |
まず分散分析を行うにあたり、色々な平均値を算出しておく必要があります。
・全体
全体 59.8
・内面的魅力の各条件の平均値
内面的魅力 低条件 66.5
内面的魅力 高条件 53.0
・身体的魅力の各条件の平均値
身体的魅力 低条件 59.5
身体的魅力 高条件 60.0
・内面的魅力×身体的魅力の各条件の平均値
内面的魅力 低 ×身体的魅力 低条件 61.0
内面的魅力 低 ×身体的魅力 高条件 72.0
内面的魅力 高 ×身体的魅力 低条件 58.0
内面的魅力 高 ×身体的魅力 高条件 48.0
次に、2要因の分散分析表を埋めていきましょう。
| 因子 | 平方和 | 自由度 | 平均平方 | F値 |
| 内面的魅力 | ② | ⑦ | 11 | 15 |
| 外見的魅力 | ③ | ⑧ | 12 | 16 |
内面的魅力✖︎外見的魅力 (交互作用) | ④ | ⑨ | 13 | 17 |
| 残差 | ⑤ | ⑩ | 14 | |
| 全体 | ① | ⑥ |
① 全体の平方和
平方和とは、それぞれのデータと平均値の差を2乗して、それらを全て足したものです。
$$(61-59.8)^{2}+(61-59.8)^{2}+(61-59.8)^{2}+(61-59.8)^{2}+\cdots(61-59.8)^{2}+(61-59.8)^{2}=3213.8$$
② 内面的魅力の平方和
一方、内面的魅力の平方和では、内面的魅力の各水準の平均値とデータ全体の平均値の差を2乗していき、それぞれのデータの個数をかけることで算出されます。
$$(66.5-59.8)^{2} \times 10+(53-59.8)^{2} \times 10=911.3$$
③ 身体的魅力の平方和
身体的魅力の平方和では、身体的魅力の各水準の平均値とデータ全体の平均値の差を2乗していき、それぞれのデータの個数をかけることで算出されます。
$$(59.5-59.8)^{2} \times 10+(60-59.8)^{2} \times 10=1.3$$
④ 内面的魅力×身体的魅力(交互作用)の平方和
内面的魅力×身体的魅力(交互作用)の平方和の求め方は、少し複雑です。
まず、内面的魅力×身体的魅力の各水準の平均値とデータ全体の平均値の差を2乗していき、それぞれのデータの個数をかけます。
$$(61-59.8)^{2} \times 5+(72-59.8)^{2} \times 5+(58-59.8)^{2} \times 5+(48-59.8)^{2} \times 5=1463.8$$
そこから、内面的魅力の平方和と身体的魅力の平方和を引くことで算出されます。
$$1463.8-911.3-1.3=551.2$$
⑤ 残差
残差は、全体の平方和から各条件や交互作用の平方和を引くことで、算出されます。
$$3213.8-911.3-1.3-551.2=1750.0$$
⑥全体の自由度
全体の自由度は、全てのデータ数から1を引くことで算出できます。
$$20-1=19$$
⑦ 内面的魅力の自由度
内面的魅力の自由度は、内面的魅力の水準数から1を引くことで算出できます。
$$2-1=1$$
⑧ 身体的魅力の自由度
身体的魅力の自由度は、身体的魅力の水準数から1を引くことで算出できます。
$$2-1=1$$
⑨内面的魅力×身体的魅力(交互作用)の自由度
内面的魅力×身体的魅力(交互作用)の自由度の求め方は、少し難しいです。
それぞれの独立変数の水準数から1を引いたものをかけることで算出されます。
$$(2-1) \times(2-1)=1$$
⑩ 残差の自由度
残差の自由度は、全体の自由度から各条件と交互作用の自由度を全て引くことで算出されます。
$$19-1-1-1=16$$
⑪ 内面的魅力の平均平方
平均平方は、平方和を自由度で割ることで算出されます。
$$911.3 \div 1=911.3$$
⑫ 身体的魅力の平均平方
$$1.3 \div 1=1.3$$
⑬内面的魅力×身体的魅力の平均平方
$$551.2 \div 1=551.2$$
⑭ 残差の平均平方
$$1750.0 \div 16=109.4$$
⑮ 内面的魅力のF値
F値は、各条件や交互作用の平均平方を残差の平均平方で割ることで算出されます。
$$911.3 \div 109.4=8.33$$
⑯ 身体的魅力のF値
$$1.3 \div 109.4=0.01$$
⑰ 内面的魅力×身体的魅力のF値
$$551.2 \div 109.4=5.04$$
これで、2要因の分散分析表の全ての値を埋めることができました。
| 因子 | 平方和 | 自由度 | 平均平方 | F値 |
| 内面的魅力 | 911.3 | 1 | 911.3 | 8.33 |
| 外見的魅力 | 1.3 | 1 | 1.3 | 0.01 |
内面的魅力✖︎外見的魅力 (交互作用) | 551.2 | 1 | 551.2 | 5.04 |
| 残差 | 1750 | 16 | 109.4 | |
| 全体 | 3213.8 | 19 |
最後に、各条件の効果や交互作用が統計的に有意かを、F分布から調べていきます。
F値で使う自由度には2つあります。
1つが条件あるいは交互作用の自由度で、もうひとつが残差の自由度です。
今回はいずれの条件も交互作用も自由度は1のため、F分布表を見るときは1つ目の自由度が1、もう1つの自由度が16のところを見ていきます。
以下のように5%水準での基準は、4.494でした。
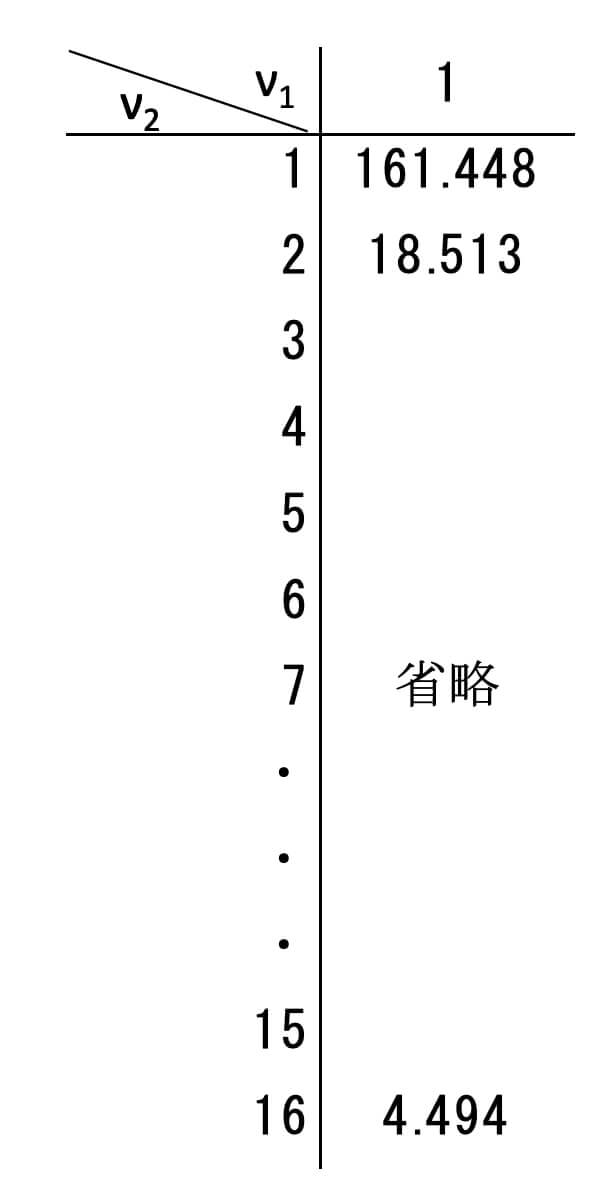
内面的魅力のF値は8.33、交互作用のF値は5.04と4.494より大きいので、内面的魅力の主効果と、内面的魅力×身体的魅力の交互作用は5%水準で有意であることが分かりました。
グラフの形と照らし合わせると、以下のことが分かります。
・内面的魅力が高い人ほど距離が近い(=好意度が高い)
・身体的魅力が低い場合は内面的魅力に距離は左右されない(=好意度は変わらない)が、身体的魅力が高い場合は内面的魅力が高いと距離が近い(=好意度が高い)が、内面的魅力が低いと距離が遠い(=好意度が低い)
カッコいい人であれば中身が多少ダメな男でも許されるというわけではないことが、この研究からは分かります。
とはいえ、きちんとした結論を出すためには多重比較を行う必要があります。
このように2要因の分散分析ではたくさんの計算を行う必要があります。
そのため、2要因の分散分析については2019年時点までの統計検定2級の過去問では出題されていません。
色々な統計初心者向け、および検定2級レベルののサイトを見てきましたが、多くの方が2要因の分散分析については出題されないんじゃないかと考えているようです。
とはいえ、統計検定2級を受験される方の目標の本質は、検定の合否以上に仕事で統計を使うことだと思います。
応用を利かせるという意味でも、2要因の分散分析を知っていて損をすることはないでしょう。
参考文献
佐藤舞(2017).身体的魅力と内面的魅力が好意度に及ぼす影響の性差 学術研究(人文科学・社会科学編)65, 111-120.
