こんにちは。産婦人科医のとみー(Twitter:@obgyntommy)です。
統計とは少し話が逸れますが、医学の領域では常により良い治療法が探求されています。(もちろん、他の分野もそうです。)
新しい治療方法が本当に有効かを確認するには、従来の治療方法と新しい治療方法を比較して評価するのが、最も直感的に理解しやすいです。(※ 本当はこんな簡単なものではないのですが、カンタンに言うと、です。)
この2つの条件の比較で最も利用される統計手法が、t検定です。
この記事では、t検定について基本から応用まで詳しく解説します。
なお回帰分析でもt検定は出てきますが、回帰分析にかかわってくるt検定については回帰分析の項目で説明します。
t検定について【まずはこれだけおさえておこう】
まずt検定について簡単に説明してから、いくつかの具体例を一緒に考えていきましょう。
この記事では以下の流れにそって、解説していきます。
t検定の理解のための大まかな流れ
- t検定の概要の理解
- t分布とは【t検定がしたがう分布】
- t検定を扱う際の前提条件
- 変化率について
t検定の概要
一言でいうと、t検定とは2つの条件・群の平均値を比較する統計的仮説検定の方法です。
母平均の差の検定とt検定は同じと考えてもらってかまいません。
2つの条件の平均値間に差が出るのは当然起こりうることです。
この差が「単なる誤差」なのか、それとも「偶然とは考えられない確率で生じた差」なのかを検証するのが、t検定の肝と言えます。
t検定のメリットのひとつに汎用性の高さが挙げられます。
先に挙げた治療法の効果判定だけではなく、製品の品質管理、マーケティングでのアンケート分析など様々な分野でt検定は用いられます。
また、サンプル数があまり多くなくても分析を行えるというのも、t検定のメリットです。
具体的にどのくらいのサンプル数があれば十分とみなせるかは学問分野によって異なりますが、分散があまり大きくなければ10個ぐらいのサンプル数でも十分に仮説検定を行えます。
t分布とは【t検定が従う分布】
t分布は正規分布と同様にベル鐘型をしています。
ただし下図の様に、標準正規分布と比べるとベルの頂点の位置が低く、若干左右の裾の位置が高いという特徴があります。
ベル型の標準正規分布の片側5%基準の面積(あるいは左右2.5%基準の面積)の中に統計値が入っていれば、それは有意な「意味のある」結果として、帰無仮説を棄却できます。
t検定ではt値というものを求めますが、そのt値の確率分布がt分布となります。
「t分布のどこに求めたt値があるのか」ということから、結果が有意となるかの判断を行います。
t検定を扱う際の前提条件
t検定を扱う際には、2つの前提条件があります。
- 間隔・比率尺度である量的データであること
- 正規分布に従うこと
いずれも、t検定が平均値というパラメーターを用いるため生じる前提です。
とはいえ、自然界や人間社会で測定するデータの多くは正規分布することが多いです。
そのため上記の前提条件があまり厳しいものではありません。
数値データであれば、t検定が使えるケースは多いです。
変化率について(t検定の代わりにはならない。)
経済学の分野では、データの値そのものよりも値の変化が重要となることは少なくありません。
変化率とは、起点の値からいくら増加あるいは減少したのかということです。
$$\text { 变化率 }=\frac{\text { 比較討象となる時点の值一起点の值 }}{\text { 起点の值 }} \times 100$$
例えば、以下の架空の会社の売上データを考えてみましょう。
| 売上(億円) | 変化率(%) |
2015年 | 10 | - |
2016年 | 15 | 150.0 |
2017年 | 18 | 120.0 |
2018年 | 20 | 111.1 |
2019年 | 30 | 150.0 |
2020年 | 25 | 83.3 |
2016年と2019年ではその前年の売上は違いますが、前の年からの変化という点ではどちらも同じ値となります。
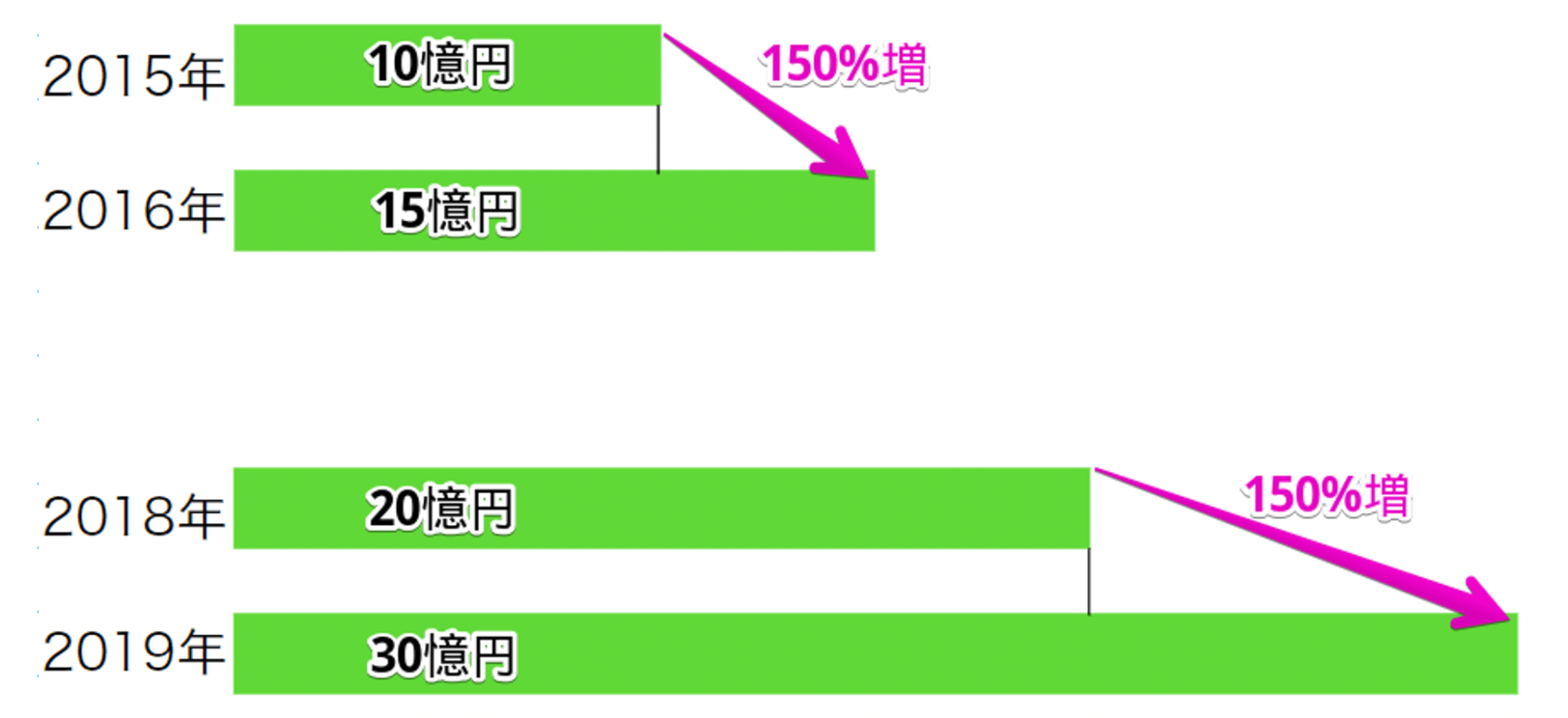
このように、変化率では基準からの変化しか分かりません。
5憶円増加した2016年も、10億円増加した2019年も同じ扱いとなります。
しかし統計的推定では、確率論を元にしてその差に意味があるか判断を下します。
そのため、変化率がどれほど大きな値でもその変化が有意と言うことはできないのです。
t検定の具体例【実際に問題を解いてみよう】
これから、いくつかの例を見ながら、t検定を扱っていきましょう。
t検定を扱う際の大まかな流れは以下の通りです。
t検定を扱う際の流れ
- 比較値を定める
- 帰無仮説の設定
- 対立仮説の設定
- 両側検定か片側検定か
- 検定統計量を算出
- 有意差の判定
実際にこの流れで進めていきます。
※ ただし、入門者向けにかなり簡略化しています。
1群の検定【このスナック菓子は本当に50g入っているのか】
ここからは、実際に問題を解きながらt検定を理解していきましょう。
t検定では2条件・群の平均値の比較を行うことが多いですが、実はひとつの母集団からランダムに取り出したサンプル群と特定の値との比較をするといったこともできます。
大量生産されたネジの大きさやお菓子の中身が均一かといったことは、この方法により調べることができます。
実際に、お菓子工場から出荷されるスナック菓子が本当に50gなのかをテーマに、検定していきましょう。
以下が、ランダムに取り出したスナック菓子の重さのデータです。
| スナック菓子の重さ(g) |
1 | 47 |
2 | 60 |
3 | 49 |
4 | 47 |
5 | 60 |
6 | 55 |
7 | 60 |
8 | 56 |
9 | 58 |
10 | 49 |
① 比較値を定める
今回は、50gが比較値となります。
② 帰無仮説の設定
「取り出してきたスナック菓子の母平均と比較値に差はない」となります。
③ 対立仮説の設定
今回の場合は母平均と比較値のどちらが大きいという方向は決められません。
そのため、「取り出してきたスナック菓子の母平均と比較値は異なる」という対立仮説を立てましょう。
④ 両側検定か片側検定か
3の対立仮説の通り、両側検定となります。
⑤ 検定統計量を算出
1群の検定の場合、以下の式から検定統計量を求めることができます。
$$\text { 検定統計量 }=\frac{\text { 標本平均 - 比較值 }}{\text { 標準誤差 }}=\frac{\text { 標本平均 - 比較值 }}{\sqrt{\frac{\text { 不偏分散 }}{\text { サンプル数 }}}}$$
※ 標準誤差とは、母集団から取り出してきた標本から標本平均を求める場合に、標本平均の値が母平均に対してどの程度ばらついているかを示すものです。
不偏分散の正の平方根を求めることで算出されます。
実際に数値を入れて計算していきましょう。
$$\frac{54.1-50}{\sqrt{\frac{30.8}{10}}}=2.34$$
⑥ 有意差の判定
今回はサンプル数が10のため、自由度10から1を引いたが9のt分布を見ていきます。
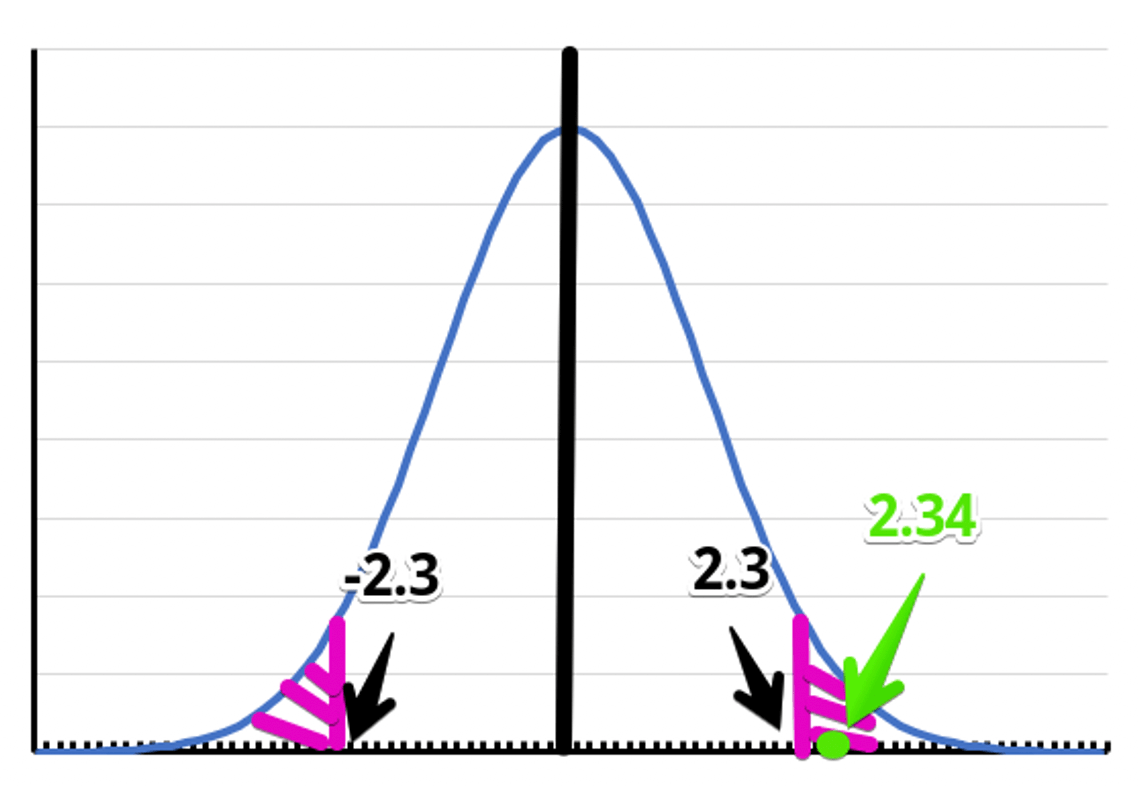
※ t分布は標準正規分布と形が非常に似ているとはいえ、サンプル数10ではここまできれいな正規分布にはなりません。
ここでは便宜上正規分布の形を取っています。
両側検定で5%水準で有意となるには±2.3以上の値になっていなければなりません。
そして、今回の検定統計量は2.34でした。そのため、有意という結果になります。
よって、「取り出してきたスナック菓子の母平均と比較値に差はない」という帰無仮説は棄却されるので、工場からお菓子は実際には50gという基準値の通り出荷されていないと判断できます。
対応のあるt検定【この降圧薬は本当に効果があるのか?】
対応のあるt検定について、新しい降圧薬の効果を検証しながら説明していきます。
なお、対応のあるt検定の「対応のある」とは、1人の被験者から2つの条件のデータを取っているということです。
2つの条件について被験者が同じではない場合は、この次の対応のないt検定を使うことになります。
以下は、降圧薬投与前と、降圧薬を1週間飲み続けた後の血圧の平均値です。
| 投与前 | 投与後 |
Aさん | 159 | 129 |
Bさん | 150 | 139 |
Cさん | 151 | 144 |
Dさん | 157 | 134 |
Eさん | 139 | 142 |
Fさん | 144 | 141 |
Gさん | 156 | 156 |
Hさん | 131 | 134 |
Iさん | 151 | 155 |
Jさん | 156 | 153 |
① 帰無仮説の設定
「降圧薬投与前と投与後の血圧に差はみられない」が帰無仮説となります。
② 対立仮説の設定
今回の場合は、降圧薬の投与後のほうが血圧が低いという方向性が仮定されます。
そのため対立仮説は、「降圧薬投与後は投与前と比べ血圧が低い」です。
③ 検定統計量を算出
対応のあるt検定の場合、以下の式から検定統計量を求めることができます。
$$\text { 統計統計量 }=\frac{\text { 条件 } 1 \text { と条件 } 2 \text { の差平均 }-\text { 差の母平均 }}{\sqrt{\frac{\text { 差の不偏分散 }}{\text { サンプル数 }}}}$$
$$=\frac{\text {投幕前後の血庄の差平均一血庄の差の母平均}}{\sqrt{\frac{\text {投慕前後の血庄の差の不偏分散}}{\text {サンフル数}}}}$$
投薬前後での血圧が変わらない(つまり、投薬前後が0)かどうかを検定するため、血圧の差の母平均=0となります。
$$\text { 検定統計量 }=\frac{6.7-0}{\sqrt{\frac{133.57}{10}}}=1.83$$
④ 有意差の判定
今回もサンプル数が10のため、自由度10から1を引いたが9のt分布を見ていきます。
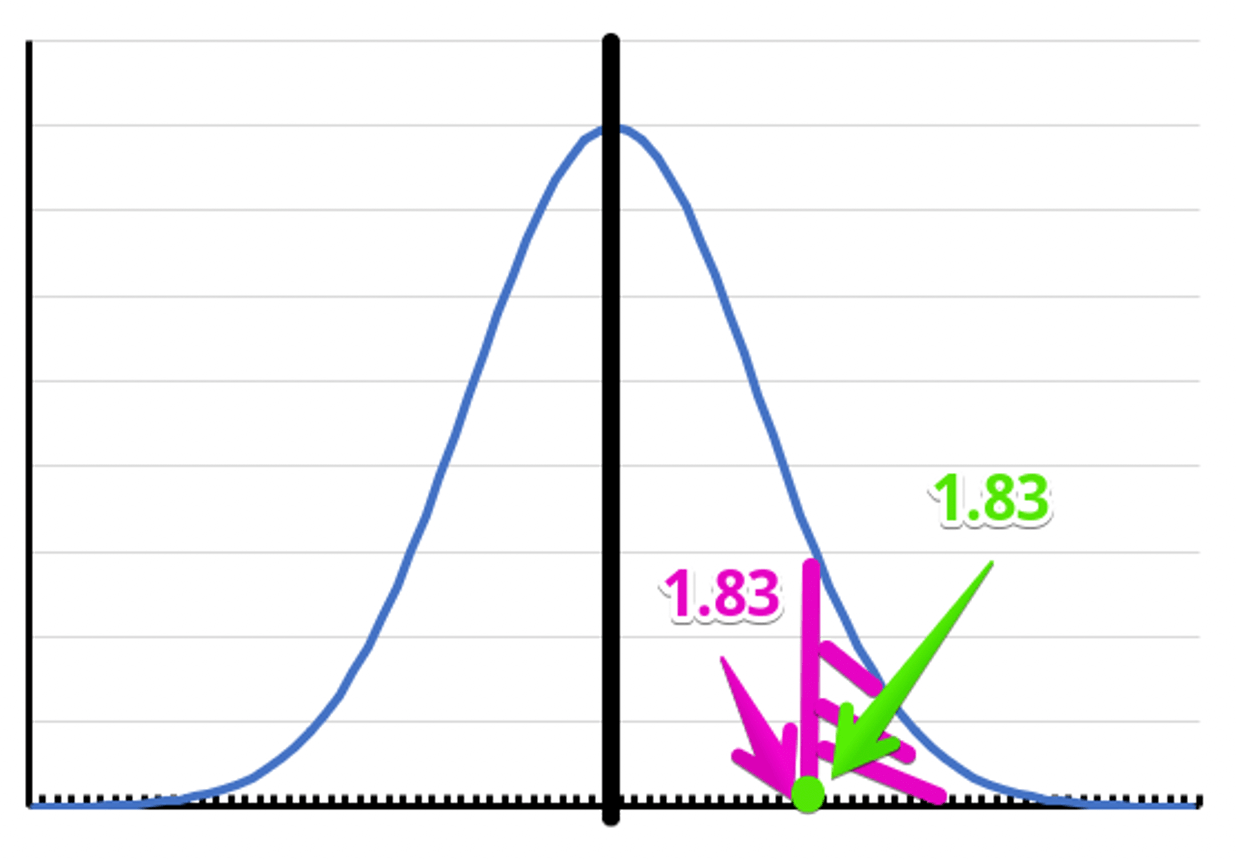
片側検定で5%水準で有意となるには1.83以上の値になっていなければなりません。
そして、今回の検定統計量は1.83でした。
そのため、有意という結果でした。
よって、「降圧薬投与前と投与後の血圧に差はみられない」という帰無仮説は棄却されるので、降圧薬投与後で血圧は下がった、すなわち新しい降圧薬は効果があったと判断されます。
対応のないt検定【この降圧薬は本当に効果があるのか?プラセボとの比較】
投薬実験の場合、「薬」の効果ではなく「薬を飲んだ」という思い込みで症状が改善されることがあります。
そのため、実際に薬を飲ませる治療群と、偽薬を飲ませる対象群を比較します。
このように一人の被験者から片方の条件のデータが取れない場合に使われる分析が、対応のないt検定です。
対応のないt検定は母分散が等しい場合と等しくない場合とで分析手法が異なります。
血圧の変化量のデータのほうが適切ですが、対応のあるt検定と結果が変わるのかも見ていけるので、先ほどと同じデータを使います。
| 条件 | 服用後の血圧 |
1 | 治療薬 | 129 |
2 | 治療薬 | 139 |
3 | 治療薬 | 144 |
4 | 治療薬 | 134 |
5 | 治療薬 | 142 |
6 | 治療薬 | 141 |
7 | 治療薬 | 156 |
8 | 治療薬 | 134 |
9 | 治療薬 | 155 |
10 | 治療薬 | 153 |
11 | 偽薬 | 159 |
12 | 偽薬 | 150 |
13 | 偽薬 | 151 |
14 | 偽薬 | 157 |
15 | 偽薬 | 139 |
16 | 偽薬 | 144 |
17 | 偽薬 | 156 |
18 | 偽薬 | 131 |
19 | 偽薬 | 151 |
20 | 偽薬 | 156 |
ウェルチのt検定【母分散が等しくない場合】
まず、母分散が等しくないと仮定されるウェルチの検定から説明します。
従来は母分散が等しいと仮定されない場合は母分散の等分散性の検定を行い、母分散が等しくなければウェルチの検定、母分散が等しければ対応のないt検定としていました。
しかし、最近では最初からウェルチのt検定を行うのが主流のようです。
① 帰無仮説の設定
「治療薬と偽薬で血圧に差はみられない」が帰無仮説となります。
② 対立仮説の設定
「治療薬の投与後のほうが偽薬の投与後よりも血圧が低い」という対立仮説を立てます。
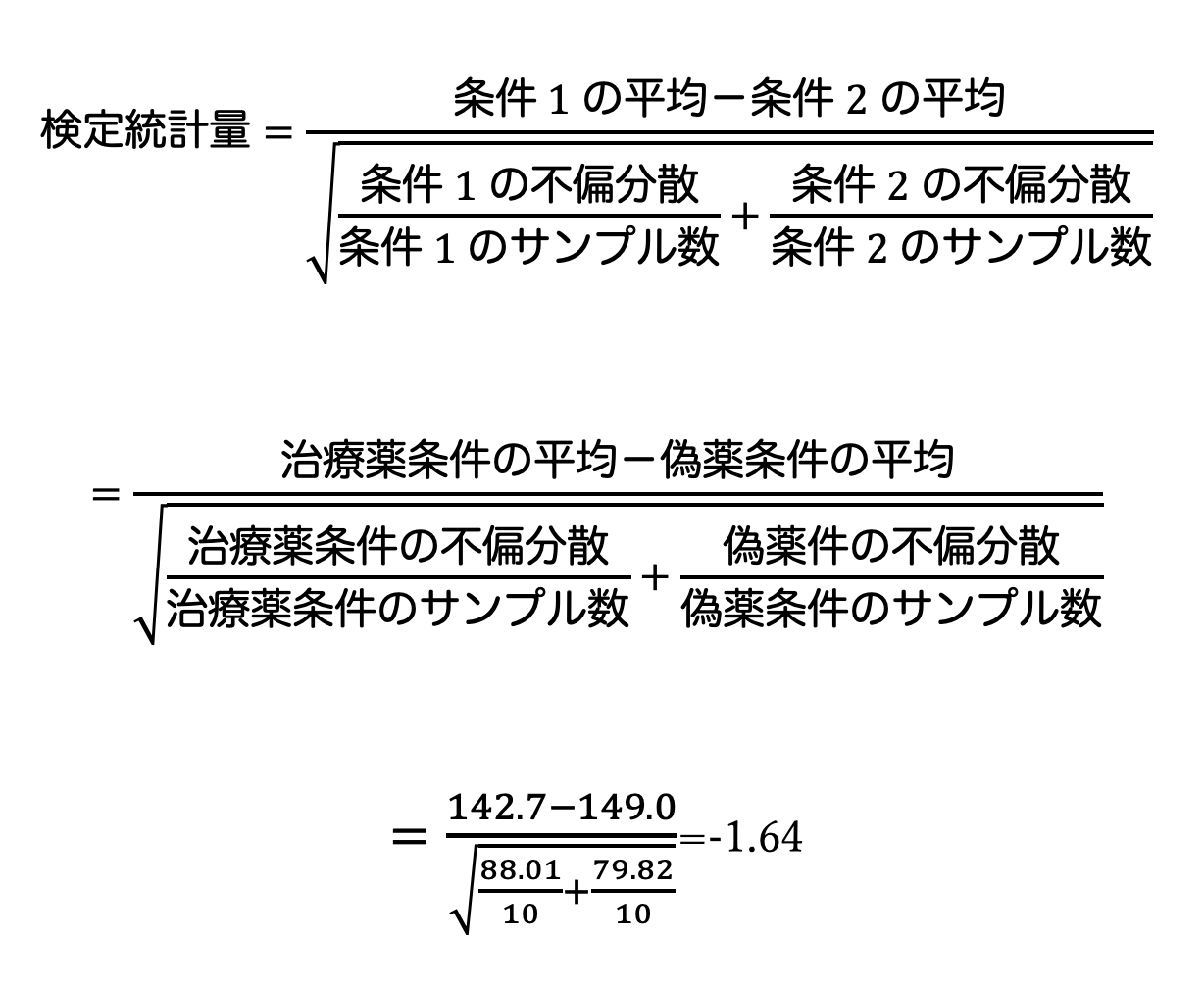
③ 検定統計量を算出
ウェルチのt検定の場合、以下の式から検定統計量を求めることができます。
④ 有意差の判定
ウェルチのt検定の場合、自由度は以下の式の近似値から求める必要があります。
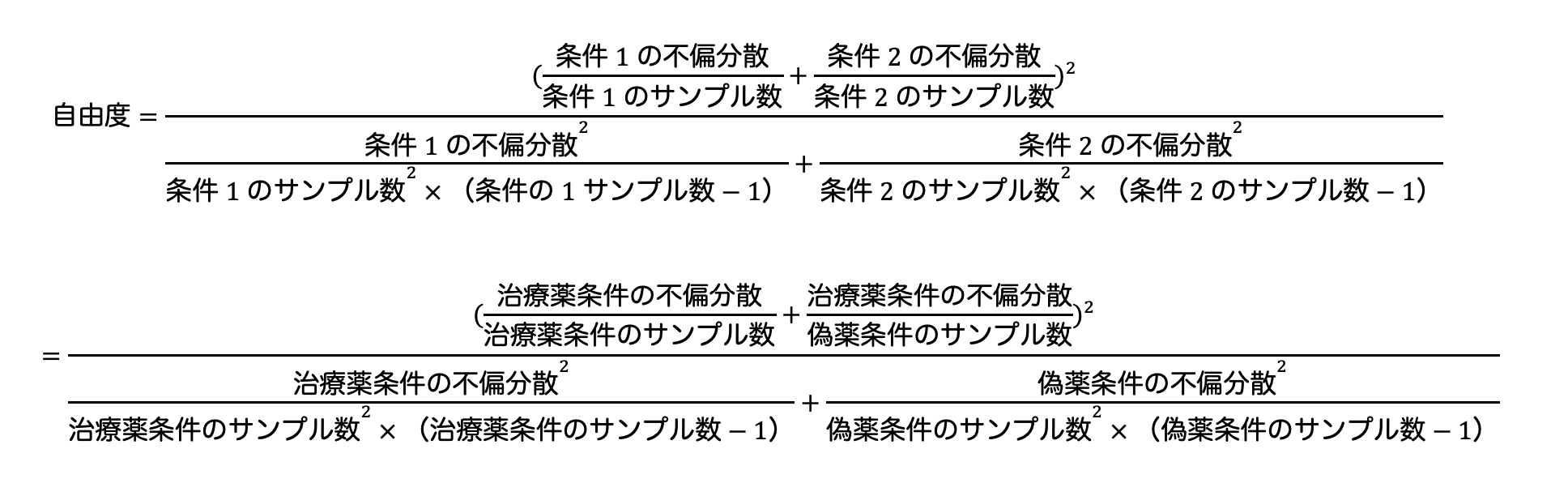 ※ 少し複雑ですので、余裕があれば理解するという程度で問題ありません。
※ 少し複雑ですので、余裕があれば理解するという程度で問題ありません。
計算の結果、自由度は17.96となりました。
自由度は17.96なので、便宜上自由度18のt分布を見ていきます。
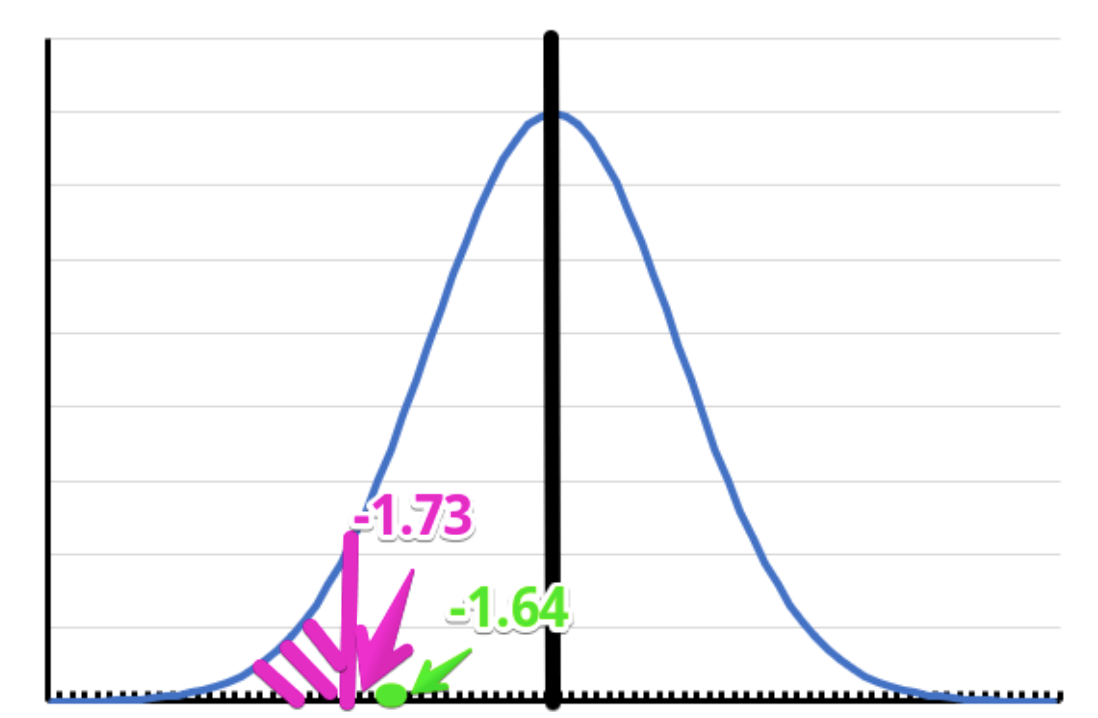
片側検定で5%水準で有意となるには-1.73以下の値になっていなければなりません。
そして、今回の検定統計量は-1.64でした。
そのため、有意という結果ではありませんでした。
よって、「治療薬と偽薬で血圧に差はみられない」という帰無仮説は棄却されませんでした。
母分散が等しい場合のt検定【対応のないt検定について】
① 帰無仮説の設定
「治療薬と偽薬で血圧に差はみられない」が帰無仮説となります。
② 対立仮説の設定
「治療薬の投与後のほうが偽薬の投与後よりも血圧が低い」という対立仮説を立てます。
③ 検定統計量を算出
対応のないt検定の場合、以下の式から検定統計量を求めることができます。

なお、プールした分散とは2つの条件の不偏分散を1つにしたものです。
プールした分散には、1つの場合と比べて分散の推定精度が高いというメリットがあります。

④ 有意差の判定
対応のないt検定の場合、自由度はそれぞれのサンプル数から1を引くので、18となります。
先ほどのウェルチのt検定と検定統計量、自由度ともに同じなので、同様に有意ではないという結果になります。
よって、「治療薬と偽薬で血圧に差はみられない」という帰無仮説は棄却されませんでした。
t検定の効果量
ここからは統計検定2級の範囲を超えていますので、参考のお話です。
» 「検定【統計学的仮説検定】とは?」
サンプル数が大きくなるほどより小さいp値の基準でもクリアして、有意という結果が得やすくなります。
独立変数の効果がどのくらい大きいのかは効果量を見なければなりません。
t検定の効果量の分析ではCohen’s dを求めます。
条件1と条件2のサンプル数が同じ場合は、以下の式から求めることができます。
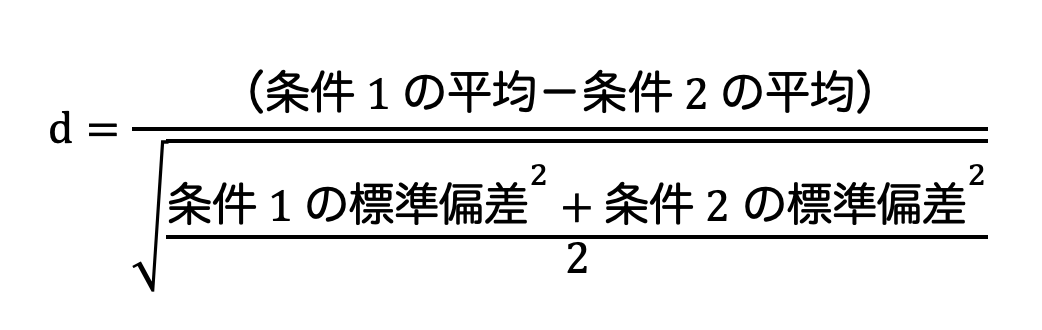
この式が意味するところは、条件1と条件2の差が標準偏差いくつ分はなれているかということです。
先ほどの対応なしのt検定の例で計算すると、d=0.73となりました。
Cohen’s dの大きさの目安は以下の通りです。
小 | 中 | 大 | |
d | 0.2 | 0.5 | 0.8 |
よって、今回の降圧薬の効果は中程度だと言えます。
【補足】自由度とは?
統計的検定を行うと、必ず「自由度」という言葉が出てきます。
自由度は $n-1$ と覚えている人は多いと思いますが、必ずしも$自由度 = n-1$とは限りません。
例えば、対応のない $t$ 検定の場合は自由度はn-2となります。
これは、自由度という統計用語を理解していると、腑に落ちます。
自由度の「自由」とは、「代表値などの数値を『自由』に決めることのできる」という意味です。
具体的に考えてみましょう。
例えば、平均値が $5$ となる3つのデータがあるとします。
適当に、1つ目の数値は $4$、2つ目の数値は $5$ としましょう。
でも、これら2つの数値を決めてしまったら、平均値が $5$ となるには残りの数値は $6$ と自動的に決まってしまいます。
これを一般化すると、$n$ 個のデータがあったときに平均値 $x$ について自由に決めることのできるデータ数は $n-1$ ということができます。
そのため、自由度といえば $n-1$ となるのです。
対応のない $t$ 検定の場合では自由度がn-2となるのは、各群でそれぞれの平均値を決めるのに1つずつ自動的に決まる値があるためです。
今回は以上となります。hh
