こんにちは。産婦人科医のtommyです(Twitter:@obgyntommy)。
この記事では、糖尿病のデータセットを用いた教師あり機械学習の一通りの流れをscikit-learnを用いて学びます。
教師あり機械学習の一般的な流れは以下の通りです。
教師あり学習の機械学習の流れ
- データセットの読み込み
- データの前処理
- 探索的データ解析(EDA;Explanatory Data Analysis)
- 機械学習予測モデルの作成
- 性能評価
scikit-learnを用いた機械学習の流れについては、以下の記事を参照して下さい。
-

【機械学習】scikit-learnの使い方【基礎から全て解説】
続きを見る
又、Google Colaboratoryの使い方については以下の記事を参照して下さい。
-

Google Colaboratoryの使い方【完全マニュアル】
続きを見る
Google Colaboratoeyを使用して学習される方は、こちらのリンクを参照して下さい。
では早速学習していきましょう。
diabetesデータセットの読み込みと内容確認

skleanのライブラリから「diabetes」のデータセットを読み込みます。
diabetesのデータセットは糖尿病患者の検査結果を基に1年後の病気の進行状況を予測するためのデータセットになります。
diabetesデータセットの中身を確認してみましょう。
In[]
1 2 3 | from sklearn.datasets import load_diabetes data_diabetes = load_diabetes() data_diabetes |
Out[]

※ 全てのデータは掲載していません。
このデータセットの中身はpythonの辞書型になっていますので、取得したい対象のキーを以下のように指定することによって、対象の中身(バリュー)を取得できます。
以下は教師データの取得を行なっています。
In[]
1 | data_diabetes["target"] |
Out[]

データの前処理

次に $X$ を特徴量、$y$ を教師データとして前処理を行なっていきます。
まずは教師データをpandasのデータフレームとしてまとめておきます。
教師データは浮動小数点数型で、詳細は公式サイトの解説にも記載がないのですが糖尿病の進行度を数値として表したものと捉えておきましょう。
In[]
1 2 3 | import pandas as pd y_all = pd.DataFrame(data_diabetes["target"],columns=["target"]) y_all.head() |
Out[]

続いて、特徴量の前処理を行います。
特徴量の名前は feature_names、値はdataキーに含まれていますのでそれを用います。
In[]
1 2 | X_all = pd.DataFrame(data_diabetes["data"],columns=data_diabetes["feature_names"]) X_all.head() |
Out[]
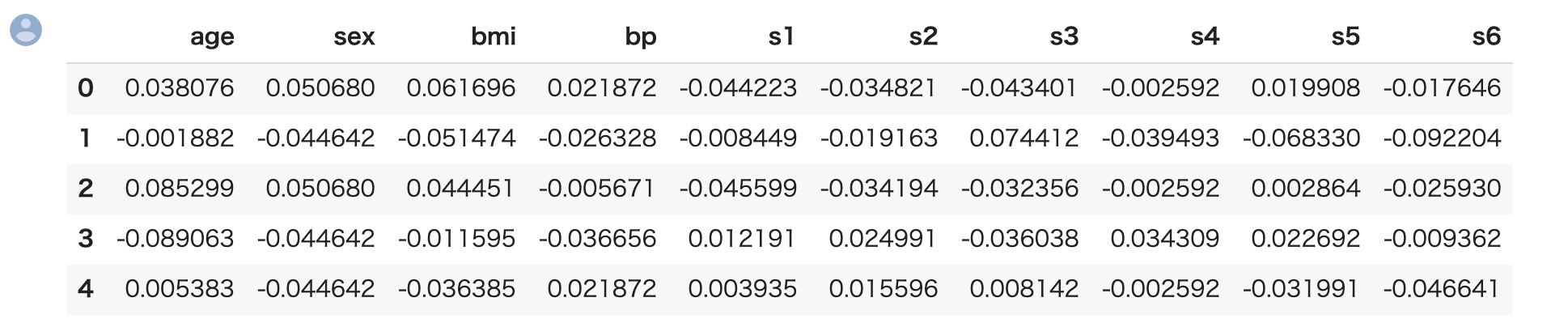
s1 から s6 について、これも公式サイトに解説がありませんが、患者の何らかの診断結果を数値化したものと捉えておきましょう。
describeメソッドによって、一括で全ての特徴量の統計値の概要を表示できます。
In[]
1 | X_all.describe() |
Out[]
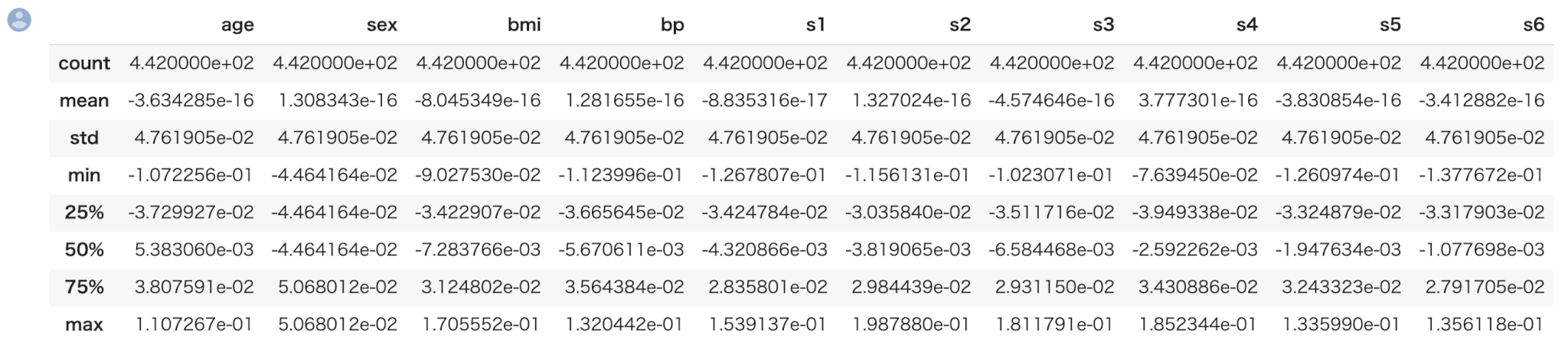
続いて、全てのデータを学習用と評価用に分割します。これにはsklearnの train_test_split メソッドを使います。
学習用データと評価用データの数の割合ですが、今回は 4:1 とします。
※ 4:1 でなければならないというわけではなく、一般的には評価用データ数が全体の2-4割程度にすることが多いです。
In[]
1 2 | from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X_all, y_all, test_size=0.2, random_state=44) |
学習データの特徴量と正解ラベルを1つのデータセットとしてまとめます。
In[]
1 | train = pd.concat([X_train,y_train],axis=1,sort=False) |
続いて、学習用データセットの特徴量と正解ラベルの型を確認します。pandas の infoメソッド により全てのカラムの型を確認できます。
In[]
1 | train.info() |
Out[]

全ての特徴量が浮動小数点数(float型)ということが確認できました。
探索的データ解析(EDA)

続いて、このデータに関して探索的データ解析(EDA)を行なっていきます。
ここで、探索的データ解析(EDA)の目的について解説します。これから機械学習を使って分類を行なっていきますが、その前に『回帰モデルによる予測が可能そうかそうでないか』を見極めるのが重要となります。
回帰モデルが有効かを見定めるにはまず教師データと各特徴量の相関を見るのが有効です。
相関(逆相関)が高い特徴量が存在するかをまずは確認してみましょう。
まず、相関を見るための相関係数の算出ですが、pandasのcorrメソッドにより一括で算出できます。
In[]
1 | train.corr() |
Out[]
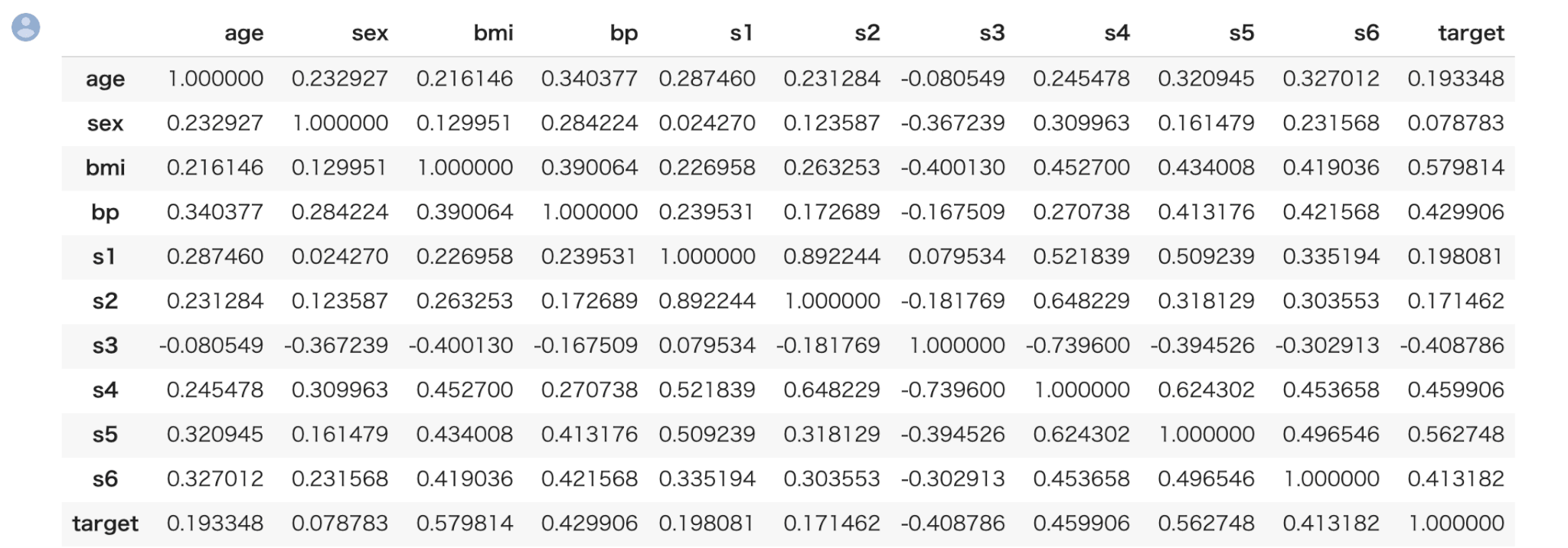
縦と横が交差するところが相関係数になります。ただ、数値のみだと見辛いのでヒートマップによる可視化が有効です。
seabornのheatmapメソッドによりヒートマップが作成できます。
引数 annot を True にすることによってヒートマップのマスの中に相関係数を表示することができます。
引数 square はヒートマップを正方形、引数 cmap はヒートマップの色を指定します。
In[]
1 2 3 4 5 | import seaborn as sns import matplotlib.pyplot as plt plt.rcParams['figure.figsize'] = (20.0, 10.0) plt.rcParams['font.family'] = "serif" sns.heatmap(train.corr(), annot=True,square=True, cmap='coolwarm') |
Out[]
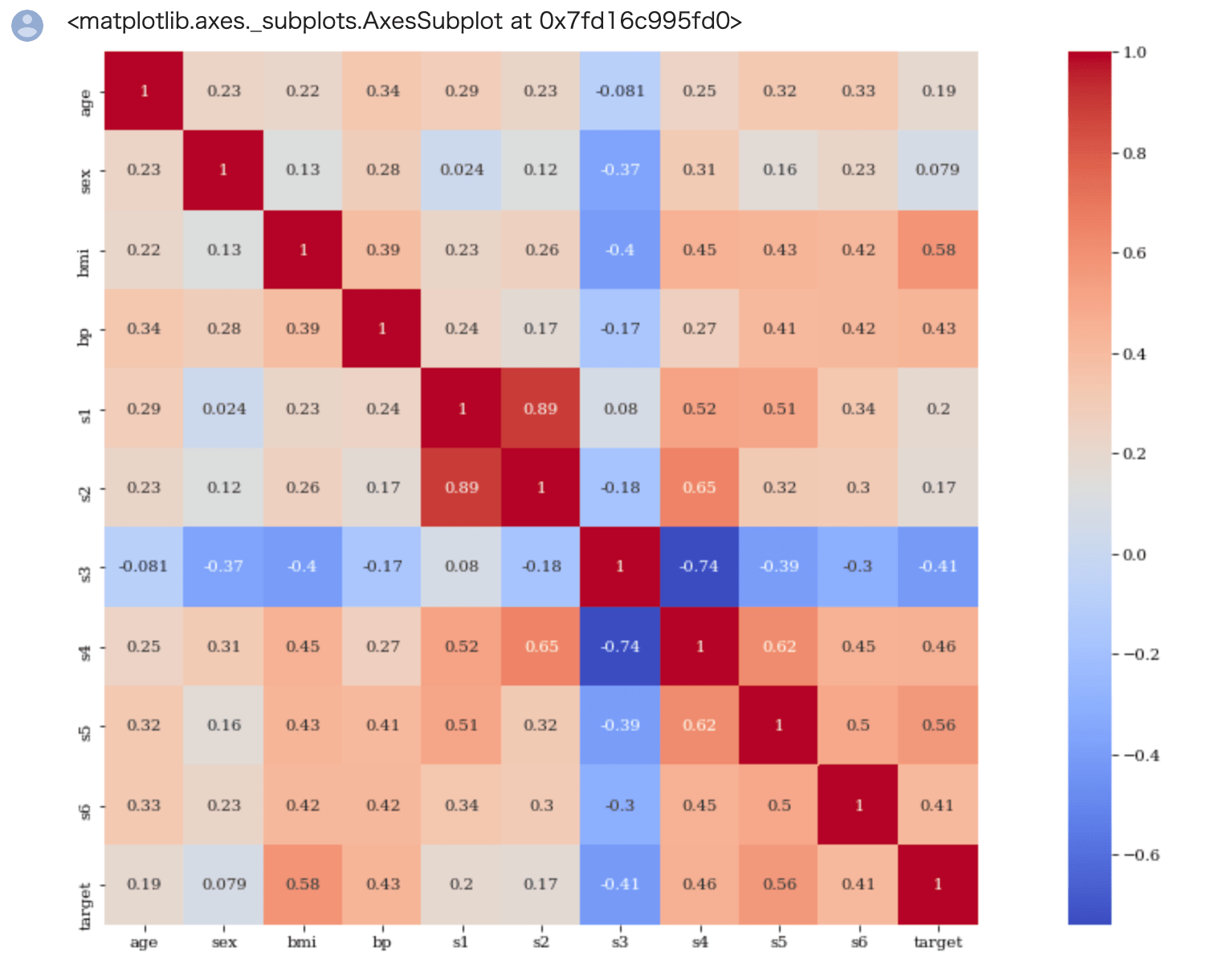
相関係数については
- 0.7以上が相関が強い(マイナスの場合は-0.7以下が逆相関が強い)
- 0.4〜0.6はまあまあ相関が強い(マイナスの場合は-0.6〜-0.4 が逆相関が強い)
という目安で良いかと思います。
targetとの相関(逆相関)を確認したいので、target列に注目します。
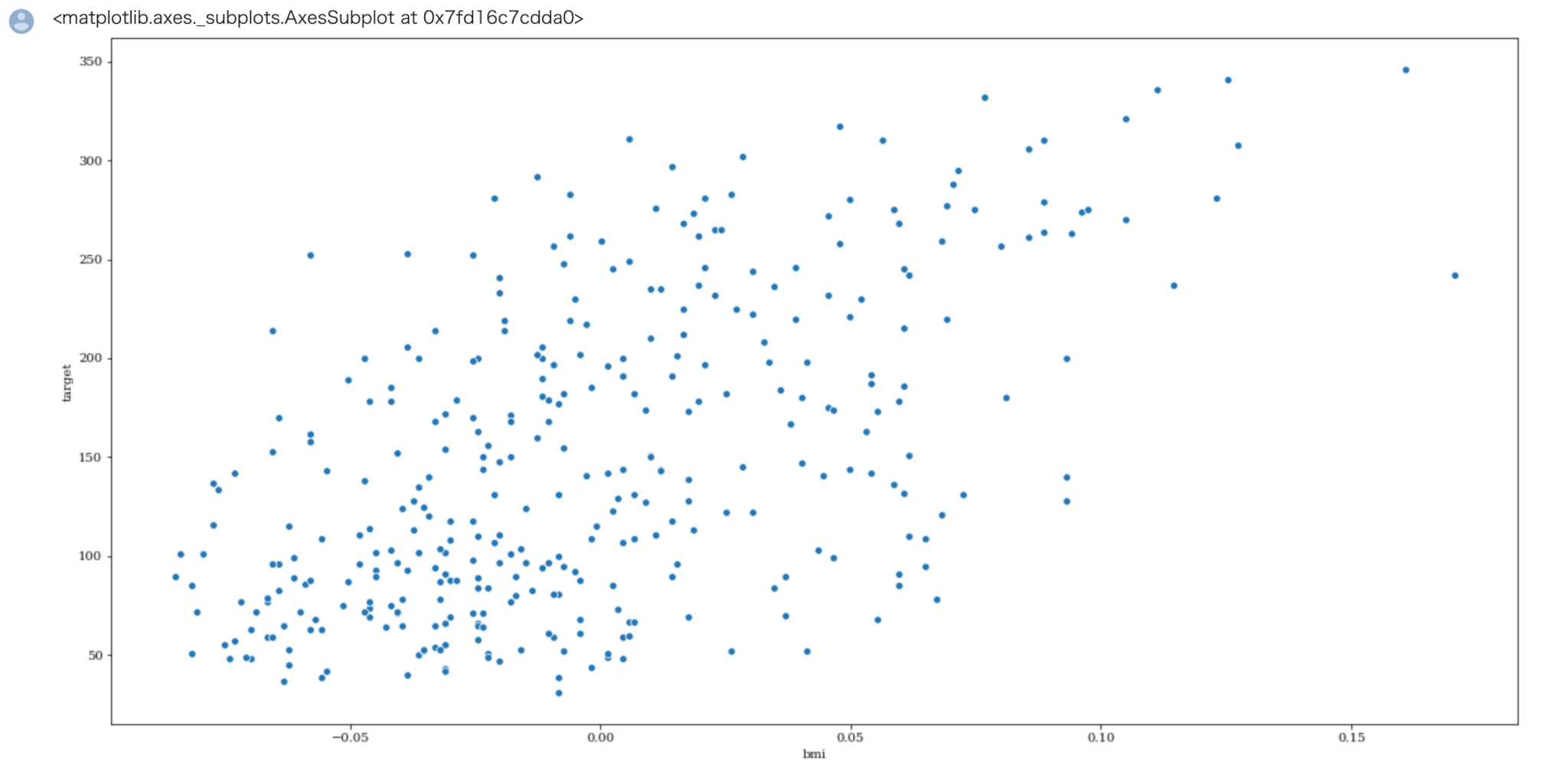
targetは bmi との相関が約0.6、s5との相関が約 0.6となっていてまぁまぁ相関があることが確認できます。
それではtargetとbmi,s5とのデータの関連性を散布図によって確認しておきましょう。
In[]
1 | sns.scatterplot( x='bmi', y="target", data=train) |
Out[]
In[]
1 | sns.scatterplot( x='s5', y="target", data=train) |
Out[]
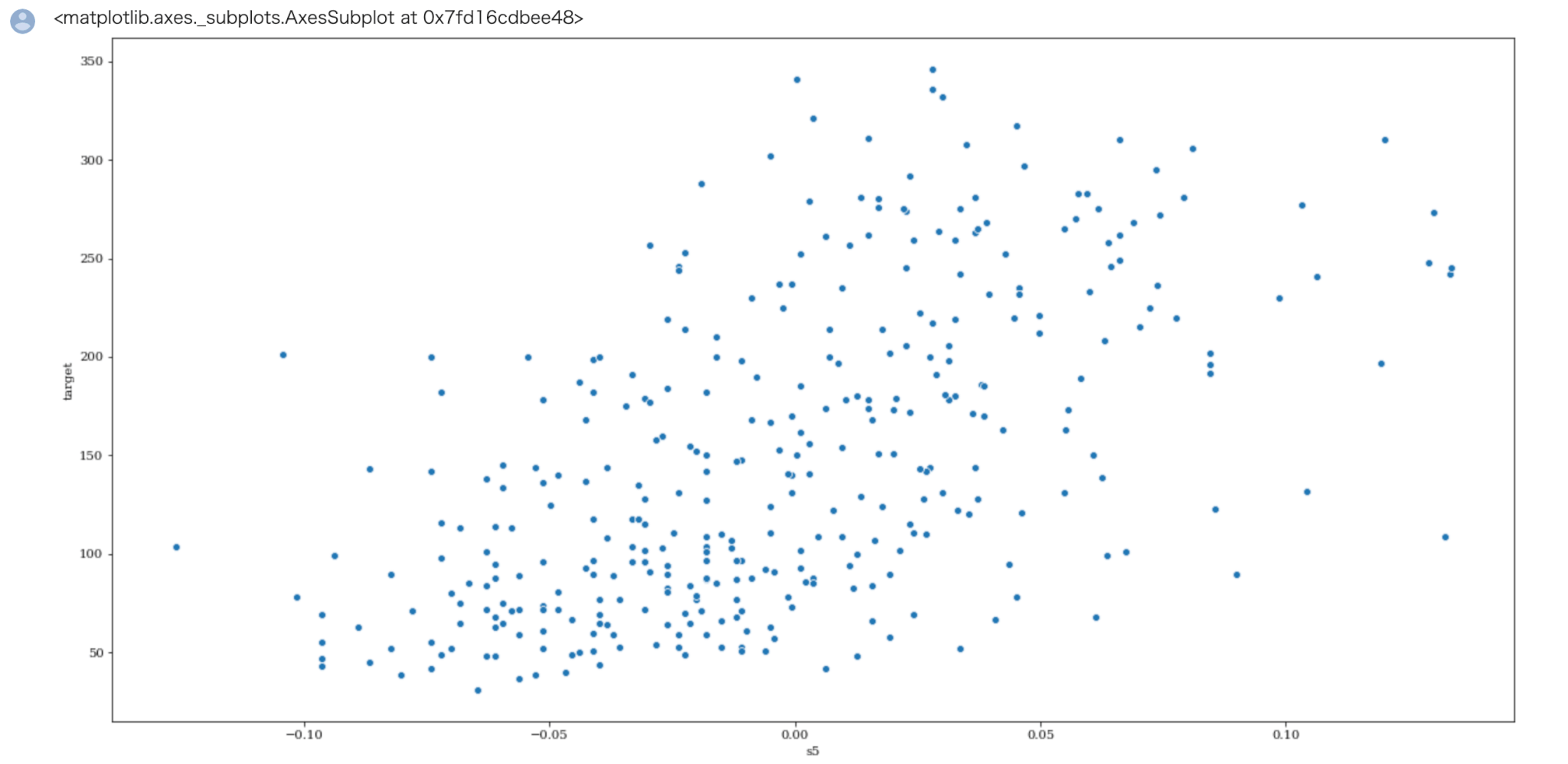
相関係数0.6ぐらいの散布図のイメージがついたのではないでしょうか。
特徴量の中には bmi , s5 の他にまあまあ相関が強い特徴量がありますので、これより機械学習モデルの作成に進んで行きます。
機械学習予測モデルの作成

機械学習予測モデルの作成を行います。すでに前処理は完了していますので、機械学習モデルのハイパーパラメータ探索から行います。
まず機械学習モデルとしてランダムフォレストを使ってみます。
ランダムフォレストも回帰木という名前で回帰用のモデルがあります。
ハイパーパラメータ探索としてグリッドサーチを用います。両方ともsklearnのクラスとして用意されています。
In[]
1 2 | from sklearn.ensemble import RandomForestRegressor from sklearn.model_selection import GridSearchCV |
ランダムフォレストのハイパーパラメータについては色々ありますが、今回は代表的なものを取り上げることにします。
max_depth(木深さ)n_estimators(木の数)min_samples_split(木ノードにおいてそれ以上分割を行うための最少サンプル数)- GridSearchCVの引数
について説明します。
scoring については今回は回帰において一般的な決定係数="r2" にしております。
cvはクロスバリデーションにおけるデータセットの分割数ですが、これは一般的には3-10くらいの場合が多いです。
もちろん分割数が多いほど結果の信頼性が高まりますが、その分計算時間が増大します。
グリッドサーチの手順としては、ハイパーパラメータの候補を作成し、それを元にグリッドサーチのインスタンスを作成、データをフィッティングさせます。
In[]
1 2 3 4 5 6 7 8 9 | param_grid = {"max_depth":[1,2,3,5,7], "n_estimators":[100,200,500],"min_samples_split":[2,3, 5,7] } reg_rf = GridSearchCV(estimator=RandomForestRegressor(random_state=0), param_grid = param_grid, scoring="r2", cv = 5, n_jobs = -1) reg_rf.fit(X_train,y_train["target"].values) |
Out[]

交差検定での決定係数の結果を確認しましょう。
In[]
1 | print("Best Model Score: ",reg_rf.best_score_) |
Out[]
![]()
決定係数約0.41ぐらいという結果になりました。より精度が上がるかというのを予測モデルを変えることで確認していきましょう。
次に機械学習モデルとしてElasticNetを用います。
ElasticNetの説明は割愛しますが、いわば従来のLasso回帰とRidge回帰のいいところどりをし、より過学習を防ぎやすいモデルと言ってよいでしょう。
ハイパーパラメータ探索としてグリッドサーチを用います。両方ともsklearnのクラスとして用意されています。
In[]
1 2 | from sklearn.linear_model import ElasticNet from sklearn.model_selection import GridSearchCV |
ElasticNetについては公式ドキュメントを確認しましょう。今回はハイパーパラメータの候補として"alpha"と"l1_ratio"を取り上げます。
alphaは学習率、すなわち学習を進ませるスピードです。大きいと計算が発散しますので一般的には出来るだけ小さくします。
l1_ratioはL1正則化の割合ですが、これはあまり意識することなく割合なので0-1の間の数を設定しておけば大丈夫です。
先ほどと同じくグリッドサーチを行います。
In[]
1 2 3 4 5 6 7 8 9 | param_grid = {'alpha': [0.00001, 0.0001, 0.001,0.01, 0.01, 0.1],'l1_ratio': [0, 0.25, 0.5, 0.75, 1]} reg_en = GridSearchCV(estimator=ElasticNet(), param_grid = param_grid, scoring="r2", cv = 5, n_jobs = -1) reg_en.fit(X_train,y_train["target"].values) |
Out[]

交差検定での決定係数の結果を確認しましょう。
In[]
1 | print("Best Model Score: ",reg_en.best_score_) |
Out[]
![]()
先ほどのランダムフォレストのモデルより少々精度が上がりました。
どのハイパーパラメータが最も良い性能を及ぼすかは、フィッティングさせたインスタンス(reg)のbest_params_メソッドで確認することができます。
In[]
1 | print("Best Model Parameter: ",reg_en.best_params_) |
Out[]
![]()
また、このハイパーパラメータを採用した際のモデルは best_estimator_メソッド により作成が可能です。
In[]
1 | reg_best = reg_en.best_estimator_ |
性能評価

続いて、予測と性能評価を行いましょう。
今回は元々性能指標として設定していた決定係数に注目することにしましょう。
決定係数は sklearn.metrics の中の r2_score で計算できます。
In[]
1 2 3 4 | from sklearn.metrics import r2_score y_pred = reg_best.predict(X_test) print(r2_score(y_test, y_pred)) |
Out[]
0.5176595852607104
さて、気になるのは決定係数約0.5が精度として信頼がおけるものなのかということです。
数学的にはこの決定係数は相関係数の2乗になります。
その為、(あまり細かいことは考えず)相関係数として捉えると大体0.7くらいになりますので、大体良い予測モデルが出来ているのではと捉えることができます。
まとめ

この記事では糖尿病のデータセットを用いた教師あり機械学習の一通りの流れをscikit-learnを用いて学びました。
Google Colaboratoeyを使用して学習される方は、以下を参照して学習して下さい。
-
Google Colab
続きを見る
今回は以上となります。
