確率分布の基礎からPythonによる実装方法まで

この記事では確率分布の基礎となる基本統計量を活用し母集団の推定を行なう方法や、Pythonによる点推定・区間推定の実装法について解説していきます。

基本統計量の基礎については基本統計量の基礎からPythonの実装までをどうぞ。

また、先日以下のツイートをしました。具体的にはこのツイートの深掘りをしていく内容となります。

🔽Pythonでの点推定・区間推定の実装
- Python超初心者の方向け

✅matplotlib、numpy、scipyを利用すると以下の算出が瞬殺です
・母平均
・母分散の点推定
・自由度
・標準誤差
・95%信頼区間

また、簡単にヒストグラムを描くことも出来るので、統計学の勉強の際に併せて上記の学習がオススメです。 pic.twitter.com/etsvL8g7y5
— 産婦人科医とみー (@obgyntommy) December 1, 2019

　本記事の内容

確率分布(正規分布)
標準誤差、標準偏差、分散
点推定、区間推定
Pythonによる実装法

では早速、見ていきましょう。

確率分布の基礎からPythonによる実装方法まで|確率分布〜標準偏差まで詳しく解説

確率分布(正規分布)とは

「基本統計量の基礎からPythonの実装まで」では、池の中にいる鯉の体⻑について考えました。

鯉の体⻑は様々な数値を取る「変数」ですが、池の中にいる鯉の母集団には様々な鯉の体長のデータがあるはずです。

重要なのは「その鯉の体長の値(変数)ごとに得る確率が存在する」ということです。

その様な様々な値を取り得る変数のことを「確率変数」と言います。

ここで池の中にいる 20000 匹の鯉(体長の平均20cm、分散1)の体⻑のバラツキについて、ヒストグラムを書いて考えてみましょう。(2万匹は少し多いかもしれませんが、大きな池を想定して下さい。)

すると、以下の様なヒストグラムを描くことができます。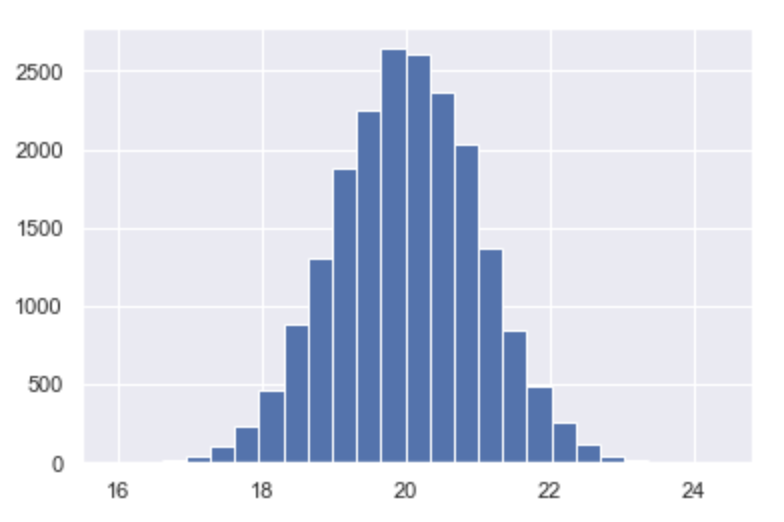
Python　点推定・区間推定　実装
体⻑が 18cm 以上 20cm 未満の魚は 20000 匹中 2660匹ですので、13.3%と言えます。

同様に、その他の体長の鯉もその鯉の体長に対応する確率があります。すなわち、鯉の体⻑は確率変数であると言えます。

また、下の表を見てください。横軸を確率変数の値として、縦軸をその確率としたグラフとなっています。

この様な「確率変数の値」と「確率」が対応したグラフを確率分布と言います。

今回の鯉の例では、鯉の体⻑は連続する値となるため、下記の⻘線のような確率分布になります。（連続値のためぶつ切りのグラフにはなりません）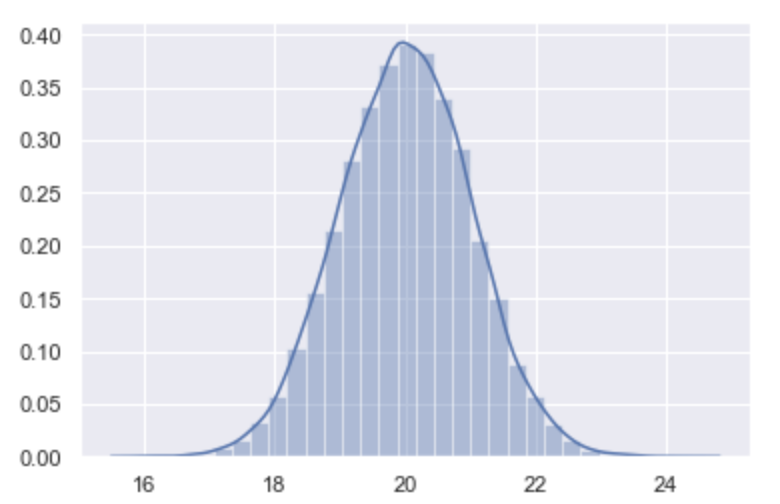

Python　点推定・区間推定　実装 ※ 横軸は鯉の体⻑ ( 確率変数 )、縦軸は確率密度

ここで、確率の数式についてまとめておきましょう。

確率変数は $X$ や $Y$ などの大文字を用いて表記します。

確率は Probability の $P$ を用いて表記するのが一般的です。

これらを用いて「18cm 以上 20cm 未満の体長の鯉が存在する確率は 13.3%」であることを数式で表すと、以下の様になります。

$$P(18≤X<20)=0.133$$

ところで、確率分布には様々な種類がありました。
» 確率分布のまとめ

この記事では正規分布(ガウス分布)について学習します。なお、正規分布に関してはこちらの記事でも詳しく解説しています。
» 正規分布(ガウス分布)とは

正規分布とは連続値をとる確率分布の 1 つで、左右対称の形をしています。横軸は確率変数、縦軸は確率変数に対応した確率密度を表します。この確率密度を定義する関数のことを確率密度関数と呼び、次の式で表されます。

$$\mathrm{f}(x)=\mathcal{N}\left(x | \mu, \sigma^{2}\right)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\left\{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right\}}$$

通常この式は $f(x)$ として表されます。

また正規分布の英訳である Normal Distribution の頭文字の N を用いて、確率密度関数は $N$ と表現します。

ところで、正規分布は平均と分散で定義されることを復習しておきましょう。

平均が $μ$、分散が $\sigma^{2}$ である正規分布のことを $N(μ, σ2)$ と書きます。

正規分布の確率密度関数について、下の図でも確認してみましょう。

$μ$ 、$\sigma^{2}$ の値を変えることにより、グラフの形も変わる事が分かります。

正規分布の確率密度関数

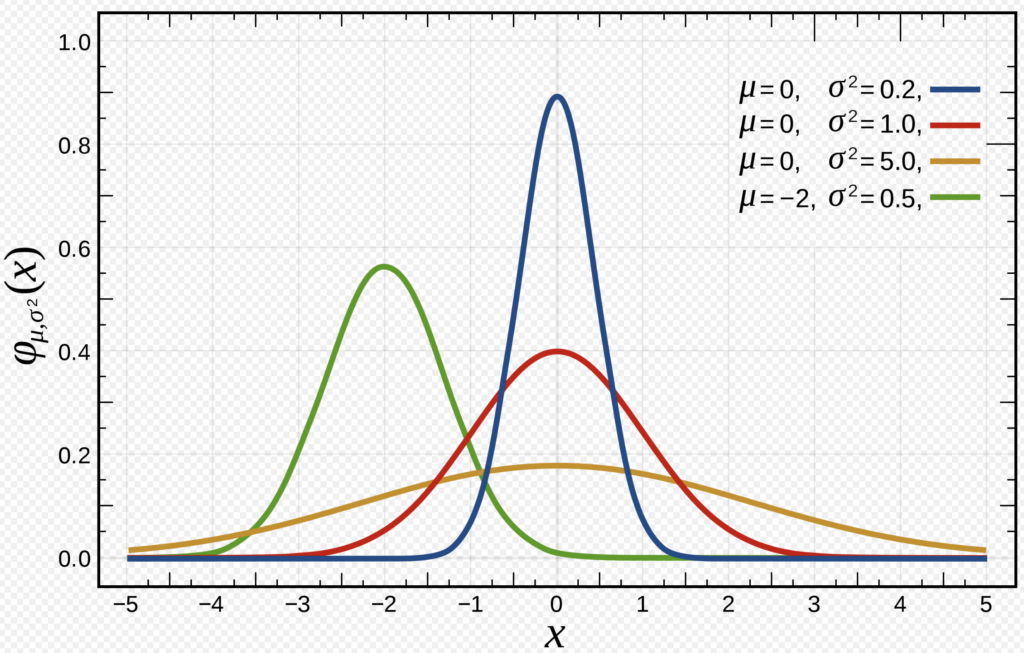
正規分布の確率密度関数。赤は標準正規分布

確率密度分布は、横軸の確率変数(がある範囲の値をとる確率)で、その範囲にわたる縦軸の確率密度関数を積分することにより求める事が出来ます。

この確率密度分布を積分したもののことを、累積分布関数といいます。累積分布関数は大文字の $F(x)$ で表現されます。また、以下の式で定義されます。

$$\mathrm{F}(x)=P(X \leq x)=\int_{-\infty}^{x} \frac{1}{\sqrt{2 \pi \sigma^{2}}} e^{\left\{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right\}} d x$$

次に累積分布関数も図で確認してみましょう。

正規分布の累積分布関数

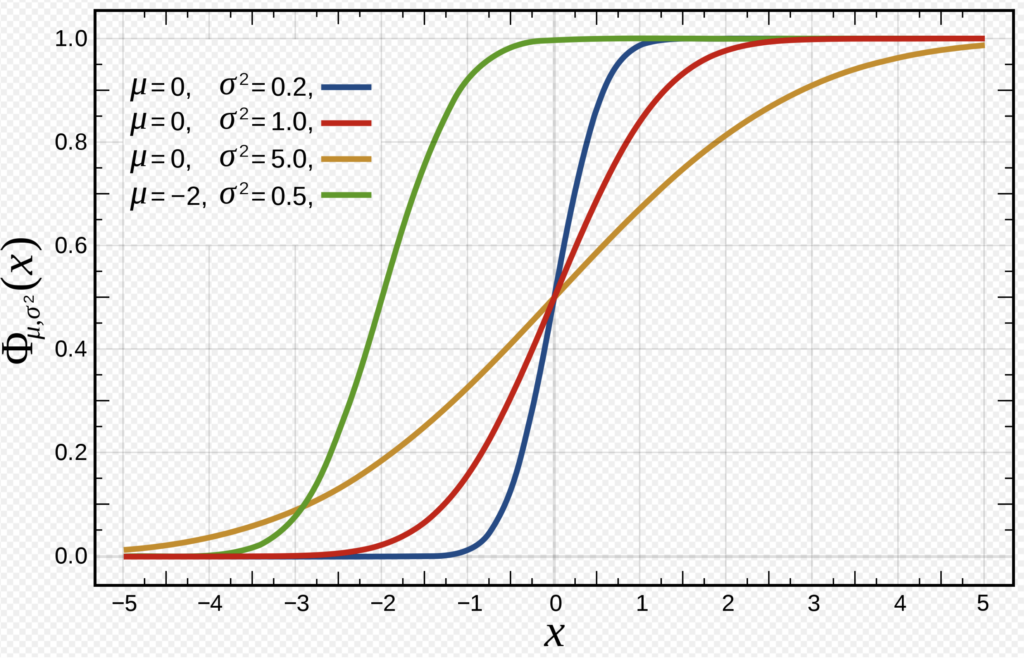
累積分布関数

ここで、池の中の鯉の設定で考えてみましょう。(この池の中にいる鯉の体長の)母集団は平均 20、分散 1 の正規分布に従うとします。この確率密度関数は下記の式として表す事が出来ます。

$$\mathrm{f}(x)=\mathcal{N}(x | 20,1)=\frac{1}{\sqrt{2 \pi}} e^{\left\{-\frac{(x-20)^{2}}{2}\right\}}$$

次に、「体⻑が 18cm 以上 20cm 未満の鯉」が存在する確率を計算してみましょう。

連続値の確率変数では $P(X=a)=0$ となりますので、$P(X<20)=P(X≤20)$とすることができます。よって下記の式が成り立ちます。

$$\mathrm{P}(18 \leq \mathrm{X} \leq 20)=\int_{18}^{20} \frac{1}{\sqrt{2 \pi}} e^{\left\{-\frac{(x-20)^{2}}{2}\right\}} d x=0.133$$

実際に手計算をすることもできます。
計算方法に興味のある方は以下を参照にしてください。
» Keisan(正規分布(区間計算))

正規分布の特徴

正規分布には、覚えておくべきルールがあります。

それは68–95–99.7 則と呼ばれるルールで、これは平均値を中心とした標準偏差の、 2 倍、4 倍、6 倍の幅に入るデータの割合の簡略化したものです。

正確には、68.27%、95.45%、 99.73%となるのですが、大まかな数字を覚えておくと便利です。図で表すと、下図のようになります。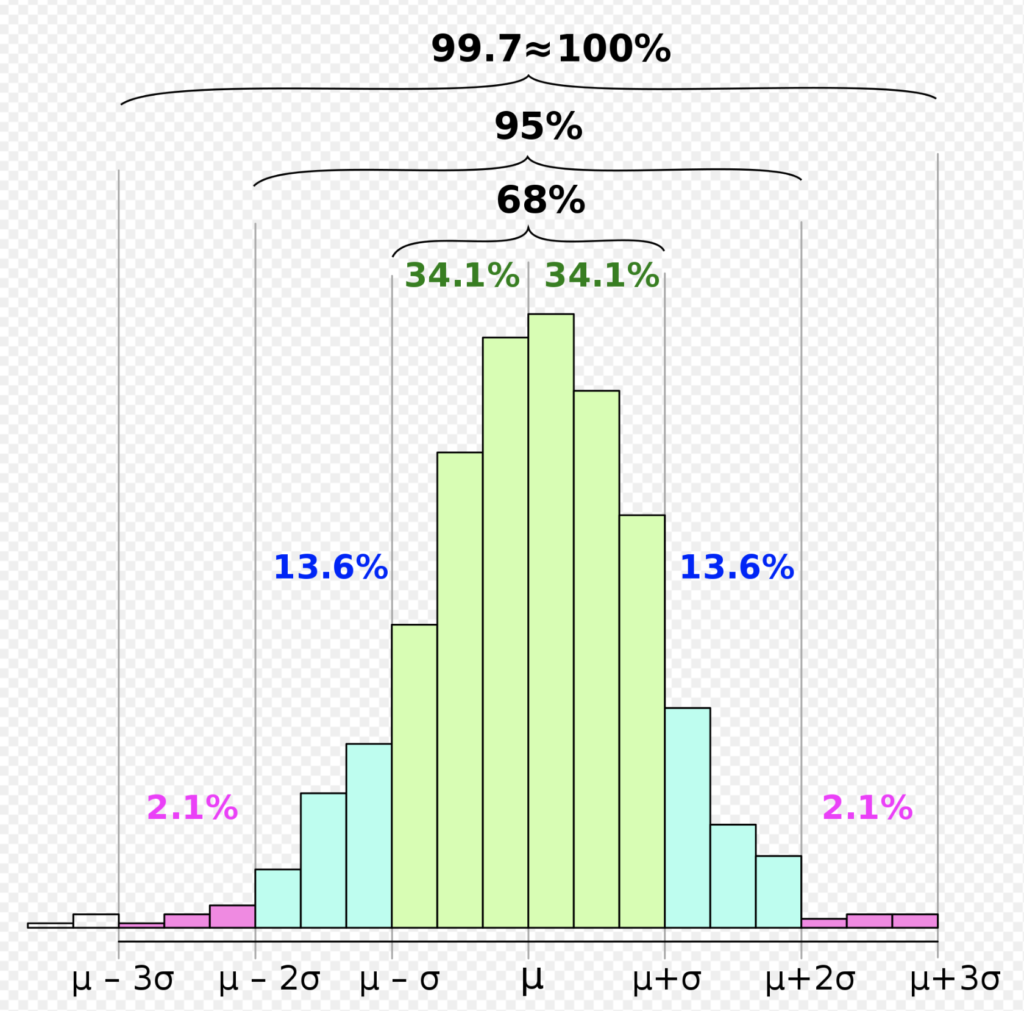

68–95–99.7則。出典: フリー百科事典『ウィキペディア（Wikipedia）』

上図は平均からの距離(標準偏差)を示しています。
「正規分布における平均からの距離とその範囲に含まれる確率」になります。

点推定・区間推定とは

推論統計とは「ある標本から未知の母集団の統計量を推定すること」でした。これは基本統計量の基礎からPythonの実装までで解説していますので、参考にどうぞ。

ここで、推定の方法には1つの値から推定する「点推定」と、ある程度の幅をもたせて推定させる「区間推定」があります。

母平均の点推定では、標本平均を母平均( $μ$ )として扱います。母分散の点推定では、不偏分散を使います。

標準誤差とは

「基本統計量の基礎からPythonの実装まで」では、標本は母集団から 1回のみサンプリングした場合を考えました。

池から鯉を何匹サンプリング(抽出)しても、1 回のサンプリングから得られる標本は 1 つだけです。今回は「複数回同じサンプリングを繰り返した場合」を考えます。

例えば池の中に 1000 匹の鯉がいたとして、この母集団から 5 匹をサンプリングして体長の平均を求めた場合、何度もサンプリングを繰り返すと平均値が変わります。

大きな魚が含まれれば平均は大きく計算されますし、小さな魚が含まれれば小さくなります。

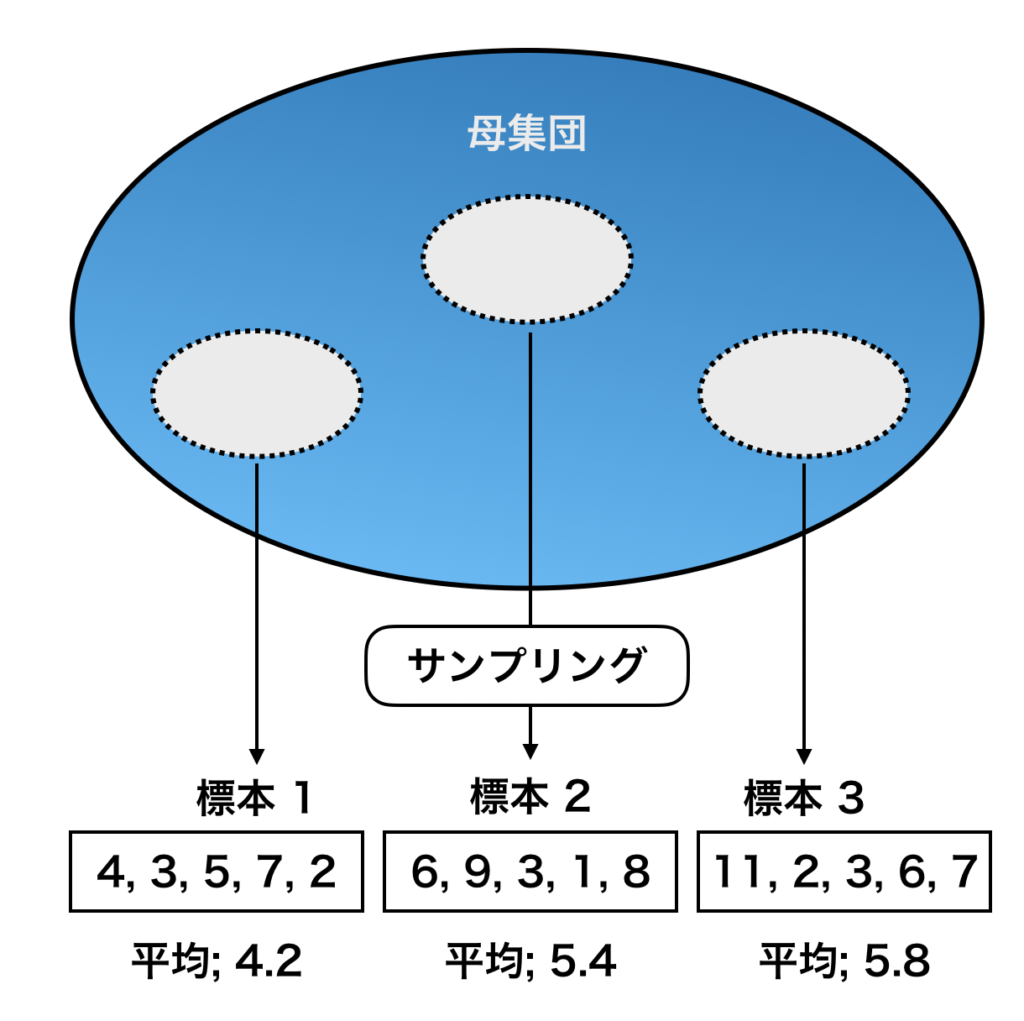
1 つの母集団からサンプリングを繰り返した場合の標本平均

このように、サンプリングを複数回繰り返すと「それぞれ異なる標本平均がサンプリングの回数分だけ得られる」事が分かります。

では、この標本平均のバラツキを知るためには何が必要となってくるのでしょうか。そこで、「中心極限定理」という定理が活躍します。

中心極限定理

中心極限定理は以下の様に定義されます。

中心極限定理

平均 $μ$ 、分散 $\sigma^{2}$ の母集団からの取り出されたサンプル数 $n$ の標本の平均( $x$ )の分布は、$n$ が十分大きければ、近似的に平均 $μ$、分散 $\sigma^{2}$ の正規分布に従う。

標本平均は平均$μ$、分散 $\frac{\sigma^{2}}{n}$ の正規分布に従うとのことですので、標準偏差は$\frac{\sigma}{\sqrt{n}}$となります。

これが標準誤差(SE)です。

$$S E=\frac{\sigma}{\sqrt{n}}$$

もし母平均・母分散が未知の場合、標本平均・不偏分散を用いる必要があります。その場合の計算式は下記の通りです。

$$S E=\frac{s}{\sqrt{n}}$$

ここまで、標本平均のバラツキについて解説しました。

ですが、本来ならば標本数が増えれば標本平均だけでなく標本分散もばらつくものです。では標本分散のばらつきは標準誤差にならないか、という疑問が出てきます。

ここで、標準誤差には広義と狭義があることを理解しておく必要があります。
広義では「 様々な推定量の精度を表す指標」
狭義では「標本平均の精度を表す指標」
と意味合いが異なります。

広義では標本分散のバラツキも意味に含まれるのですが、狭義では含まれません。また通常、「標準誤差」と言う場合にはこの狭義の意味を指します。

今後「標準誤差」と言われば場合には「標本平均の標準偏差」と考えておくと良いでしょう。

区間推定

サンプリングを繰り返して複数の標本を入手することで情報の数が増えるのは理解できましたが、ここからどのように母集団の基本統計量を推定したら良いのか解説していきます。

まずは母平均について考えてみましょう。先ほどの中心極限定理を用いますと、標本平均の分布が推定できます。

その標本平均の分布が平均 $\bar{x}$、分散$\frac{s^{2}}{n}$ の正規分布ということです。それでは、先ほどの池の中の鯉の例で考えてみましょう。

16 匹の魚をサンプリングした結果、平均が 20cm, 分散が 1 だとします。そうするとこの池の魚の標本平均は平均 15cm、分散 0.75の正規分布に従うとわかります。先ほど学習した確率分布を書いてみましょう。

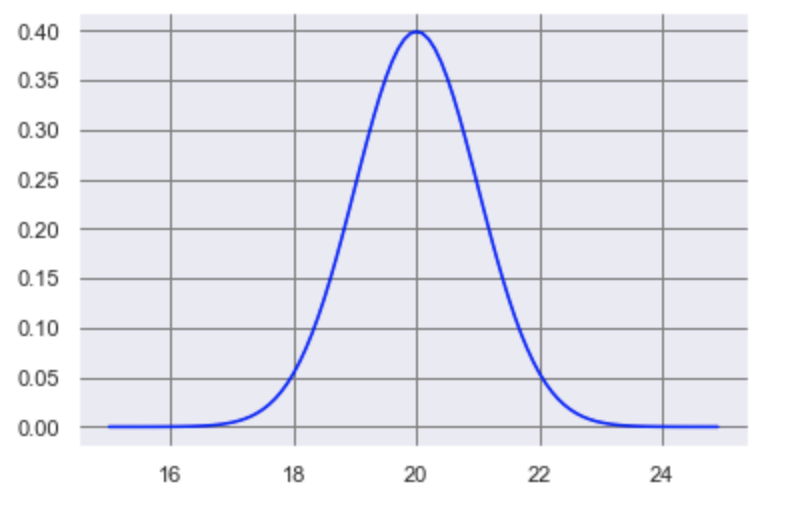
標本平均の確率分布

上の確率分布は標本平均について書かれているものです。これに先ほど学習した「(標本平均 - 母平均)/標準偏差」で求められる「その範囲に入る確率」を考えると、たとえば「標本平均はこの範囲内に 95%の確率で入る」ということが言えるようになります。

これを母平均として考えると、「母平均はこの範囲内に 95%の確率で入る」と言えます。

また、この範囲、信頼区間の下限値を下側信頼限界、上限値を上側信頼限界と呼びます。

(標本平均 -母平均)/標準偏差」を今後は $t$ 値と呼びます。ネット上では「標準正規分布表」で検索すると色々と出てきます。ですが Python を使うと非常に簡単なので、Pythonで実装してみましょう。

上記の確率分布もPythonで作図しました。簡単なコードですので、このままコピペして作図してみてください。

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
 
# グリッドON
plt.grid(color='gray')
 
# 平均
loc = 20
# 標準偏差
scale = 1
 
# 左端（平均-5*σ）
start = loc - scale * 5
 
# 右端（平均+5*σ）
end = loc + scale * 5
 
# X軸
X = np.arange(start, end, 0.1)
# 正規分布pdf生成
Y = norm.pdf(X, loc=loc, scale=scale)
# プロットする
plt.plot(X, Y, color='blue')
plt.show()

import numpy as np

from scipy.stats import norm

import matplotlib.pyplot as plt

# グリッドON

plt.grid(color='gray')

# 平均

loc = 20

# 標準偏差

scale = 1

# 左端（平均-5*σ）

start = loc - scale * 5

# 右端（平均+5*σ）

end = loc + scale * 5

# X軸

X = np.arange(start, end, 0.1)

# 正規分布pdf生成

Y = norm.pdf(X, loc=loc, scale=scale)

# プロットする

plt.plot(X, Y, color='blue')

plt.show()

このコードで上の表を作図する事が出来ます。また、左端、右端の幅や平均、標準偏差を自身で変化させてみて確率分布が変わるのを実感してみてください。

Pythonで実装してみる

早速Pythonで実装してみましょう。

■ モジュールをインポート

In[]

import numpy as np 
import scipy as sp
import matplotlib.pyplot as plt
from scipy import stats

import numpy as np

import scipy as sp

import matplotlib.pyplot as plt

from scipy import stats

In[]

import seaborn as sns
sns.set()

1 2	import seaborn as sns sns.set()

seaborn は matplotlib と同じくグラフを表示するのに使うライブラリです。matplotlib より綺麗なグラフを表示できる反面、引数の指定方法などが matplotlib と異なるグラフも多くあります。seaborn も非常に使い易いライブラリですので、seaborn について詳しくは公式ドキュメントを参照してください。

» seaborn API reference

■ 乱数を発生させる

In[]

np.random.seed(20191202)

1	np.random.seed(20191202)

この seed というのは、乱数種を指定する関数です。乱数種を指定しないと、毎回異なる乱数が生成されます。多くの場合、乱数は欲しいと同時に再現性も求められます。この seed を設定しておくと、常に同じ乱数が生成されます。ここれは乱数種を 20191202 としましたが、 1でも10でも数字であれば何でも自由に決めて構いません。

■ 次に、平均 20、分散 1 の正規分布に従う乱数を 20000 個発生させます。
In[]

norm_dist = stats.norm(loc = 20, scale = 1) 
data1 = norm_dist.rvs(size = 20000)

1 2	norm_dist = stats.norm(loc = 20, scale = 1) data1 = norm_dist.rvs(size = 20000)

■ 結果を確認します。

In[]

data1

data1

Out[]

array([19.46269541, 19.75387976, 19.90202659, ..., 19.83138088,
       20.7450051 , 21.03865158])

1 2	array([19.46269541, 19.75387976, 19.90202659, ..., 19.83138088, 20.7450051 , 21.03865158])

■ matplotlib でヒストグラムを作成

In[]

plt.hist(data1,bins=25)

1	plt.hist(data1,bins=25)

柱の数を上記の25columnから30columnへと変更したい場合には、 plt.hist(data1, bins=30)と指定します。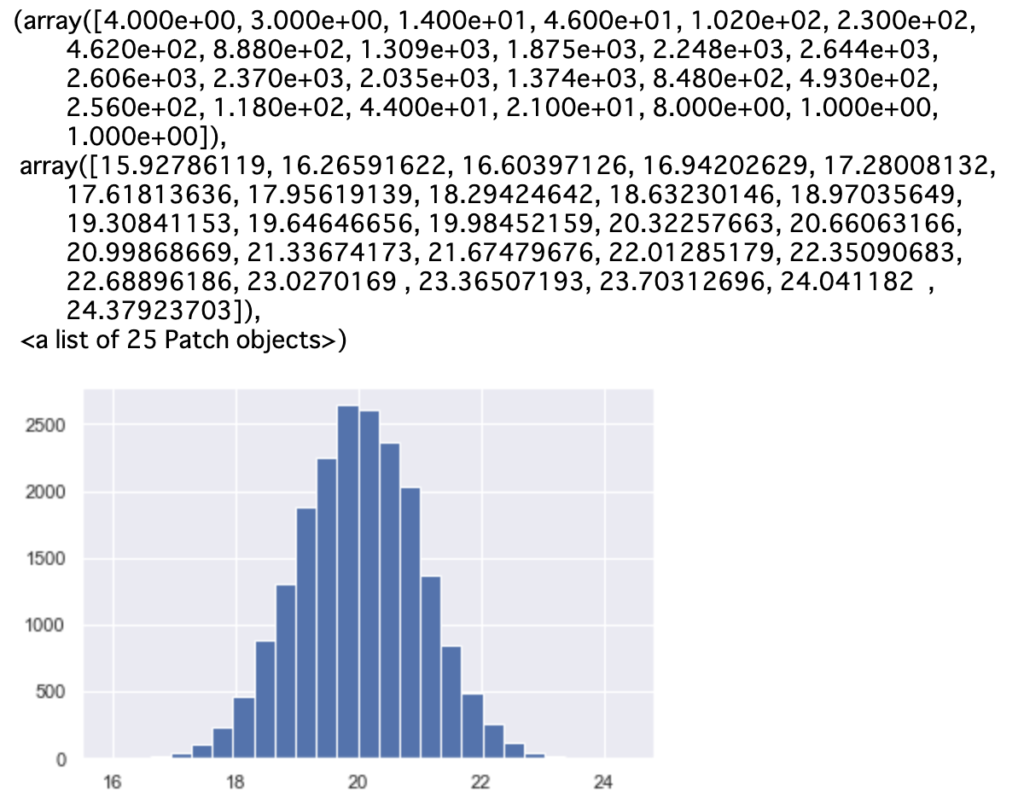

Python　点推定・区間推定　実装
■ ヒストグラムに分布を上書きしてみましょう。

In[]

sns.distplot(data1, bins=30)

1	sns.distplot(data1, bins=30)

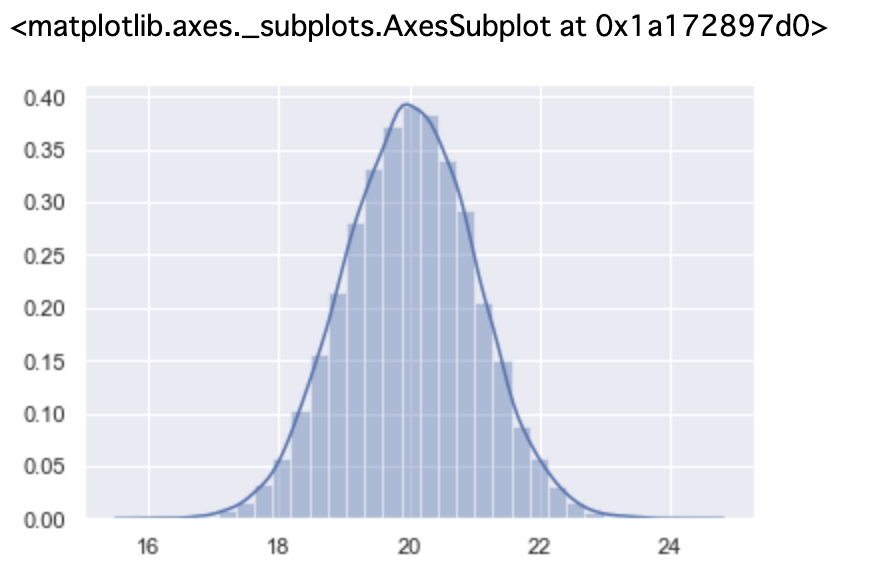
Python　点推定・区間推定　実装

■ 母平均の点推定

In[]

mu = sp.mean(data1) 
mu

1 2	mu = sp.mean(data1) mu

Out[]

20.00372463211496

1	20.00372463211496

■ 母分散の点推定

In[]

sigma2 = sp.var(data1, ddof=1) 
sigma2

1 2	sigma2 = sp.var(data1, ddof=1) sigma2

Out[]

1.0048611828595946

1	1.0048611828595946

■ 自由度の計算

In[]

df = len(data1)-1 
df

1 2	df = len(data1)-1 df

Out[]

19999

19999

■ 標準誤差の計算

In[]

sigma = sp.std(data1, ddof=1)
se = sigma/sp.sqrt(len(data1))
se

sigma = sp.std(data1, ddof=1)

se = sigma/sp.sqrt(len(data1))

Out[]

0.007088233852165131

1	0.007088233852165131

■ 95%信頼区間の計算

In[]

interval = stats.t.interval(alpha=0.95, df=df, loc=mu, scale = se) 
interval

1 2	interval = stats.t.interval(alpha=0.95, df=df, loc=mu, scale = se) interval

Out[]

(19.989831108197993, 20.017618156031926)

1	(19.989831108197993, 20.017618156031926)

まとめ

この記事では、母平均の点推定と区間推定の考え方、標準偏差、分散の復習や、正規分布とそれを応用した母平均の信頼区間の計算方法についても学習しました。

正規分布は今後もよく使用するので、繰り返し復習して理解しておきましょう。