こんにちわ。
前回【Python】プロ野球選手の年俸を予測において散布図の描き方について解説しました。
この記事は【Python】プロ野球選手の年俸を予測を読んで頂ければより理解が深まる様になっています。
この記事では、プロ野球の記事に引き続き、線形モデルの解説から最適化問題を評価関数(損失関数)で解決する方法を解説していきます。
最適化学習において重要な線形モデルとは

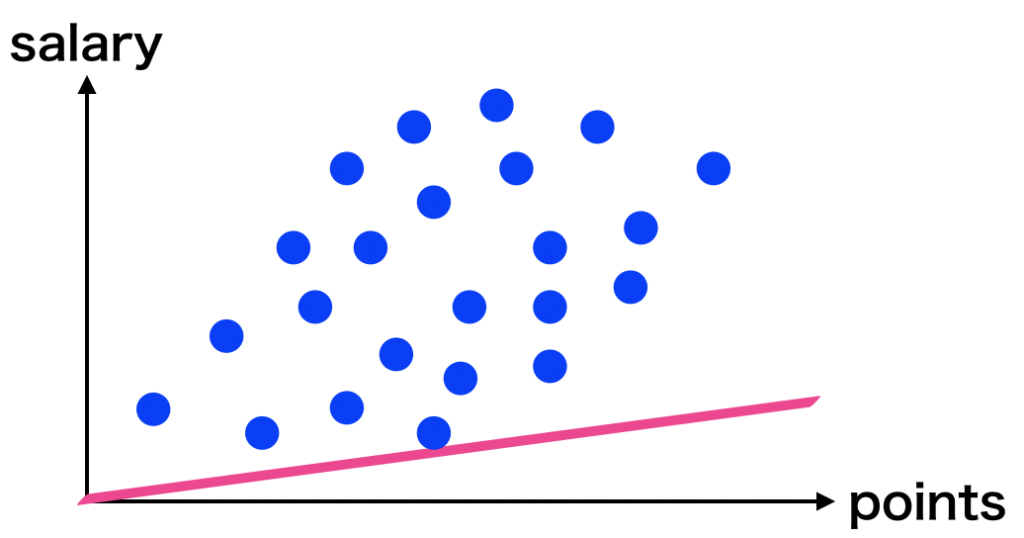
プロ野球の記事で描図した図は以下の様な散布図になります。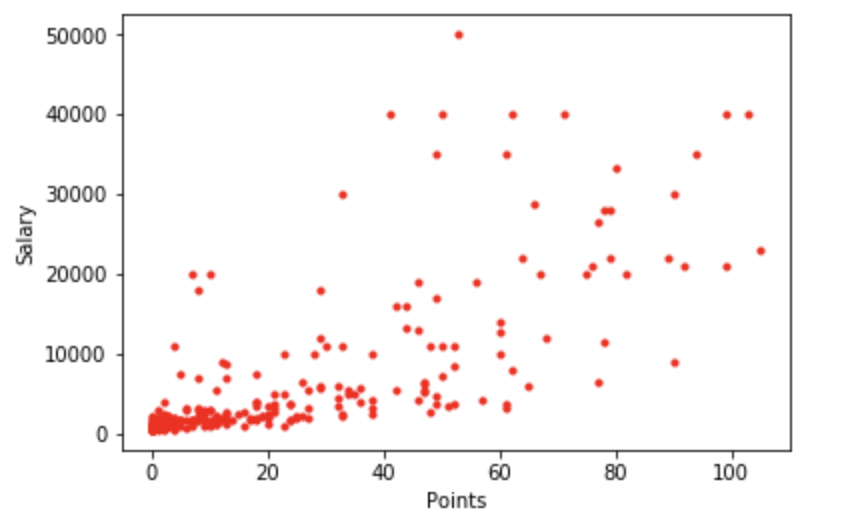
この描図を少しぼーっと眺めてみてください。この散布図のモデルはどの様な相関があるでしょうか。
もし一本直線でモデル化ができれば、野球選手の「打率」と「値段」が比例している事が分かります。
年俸が $S$ 、打点が $P$ であるとすると、直線化をする際には年俸 $S$ が $P$ に比例すれば良いですよね。
$$S=a \times P+b$$
上の式を線形のグラフで表すと以下の様になります。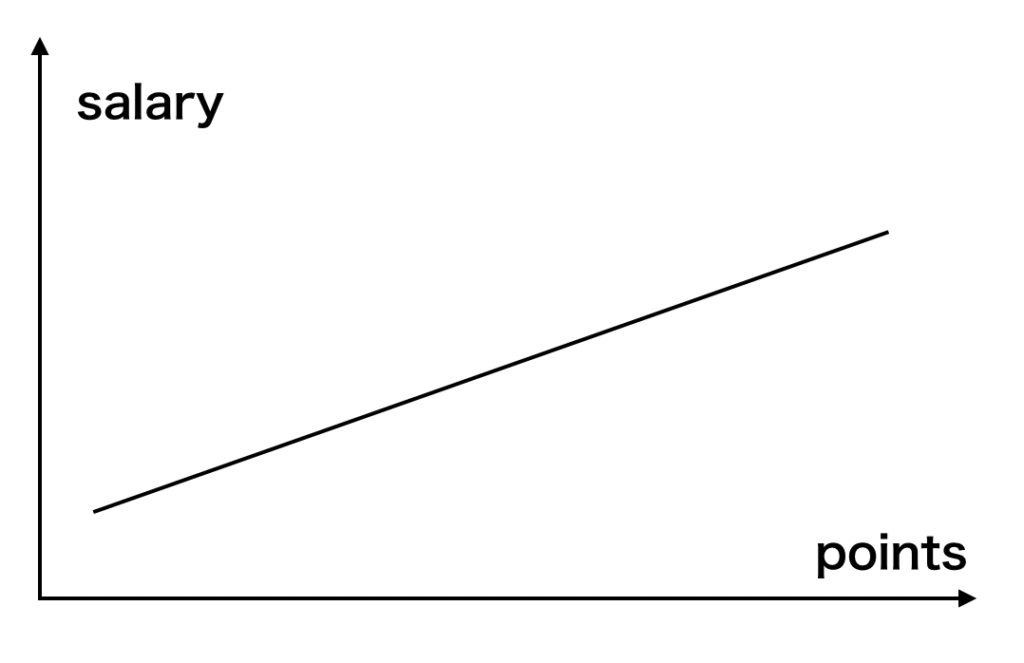
- 見たままなのですが、このモデルは「線形モデル」と呼ばれます。
- 線形モデルにデータに落とし込む方法を「線形回帰」と呼びます。
最適化問題の本質を捉える

先程紹介したこの式について再度考えてみましょう。
$$(S=a \times P+b$$
$S$ は年俸を、$P$ は打点を意味します。そこで、係数 $a$ と $b$ はどのように決定すれば良いのでしょうか。
係数 $a$ と $b$ を決定する際に出てくる問題は、散布図に散在しているデータに合ったモデルをどのように見つければ良いかという点です。
この問題の事を最適化問題と言います。最適化問題を解決するためのポイントは以下の2点です。
- モデルの適性を評価する評価関数(損失関数)を作る
- 評価関数を最大あるいは最小にする係数 $a$ と $b$の組み合わせを計算する
ここで評価関数を最小化するための方法は、以下の記事にまとめていますので是非読んでみてください。
この記事と合わせて読んでいただくと理解が深まると思います。
評価関数(損失関数)でモデル適性を評価する

「評価関数」とは、「データに対するモデル(線形モデルなど)の正確さ・適正さを評価するための関数」のことで、損失関数とも言うことができます。
» 単回帰分析と最小2乗法の求め方
今回の場合、データセット \(\mathcal{D}\) に対してパラメータ=係数 $(a, b)$ が持つ線形モデルを仮定しています。
そこで考えていただきたいのが「モデルの適切さ」です。例えば、もう一度以下の散布図を見てみてください。
 散布図に対してモデルの線形モデルが適切かどうか、をどの様にして考えていけば良いのでしょうか。
散布図に対してモデルの線形モデルが適切かどうか、をどの様にして考えていけば良いのでしょうか。
定番な方法として、モデルの直線から散布ずの各点までの距離を用いた方法を使います。直線の式は以下の様になっています。
直線モデル: \(\hat{S}=a \times P+b\)
直線式と散布図のデータ\(\mathcal{D}\) との距離を計算して、最も距離の近いパラメータ(係数)が適切であるという考え方です。
まずは下の3つのグラフを見てください。これらは、ランダムに$a$ と $b$ の値を設定してデータと一緒にプロットしたものです。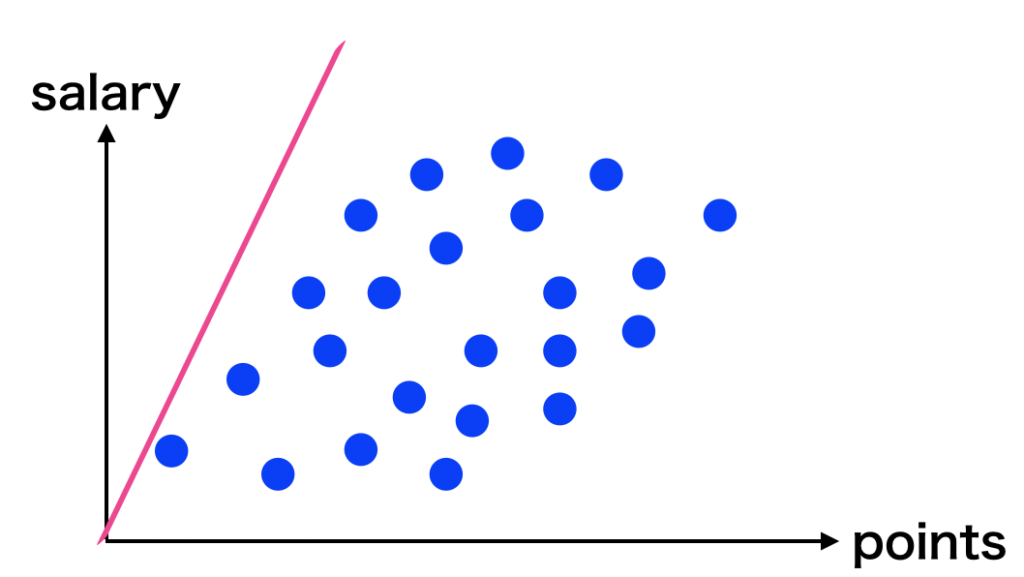
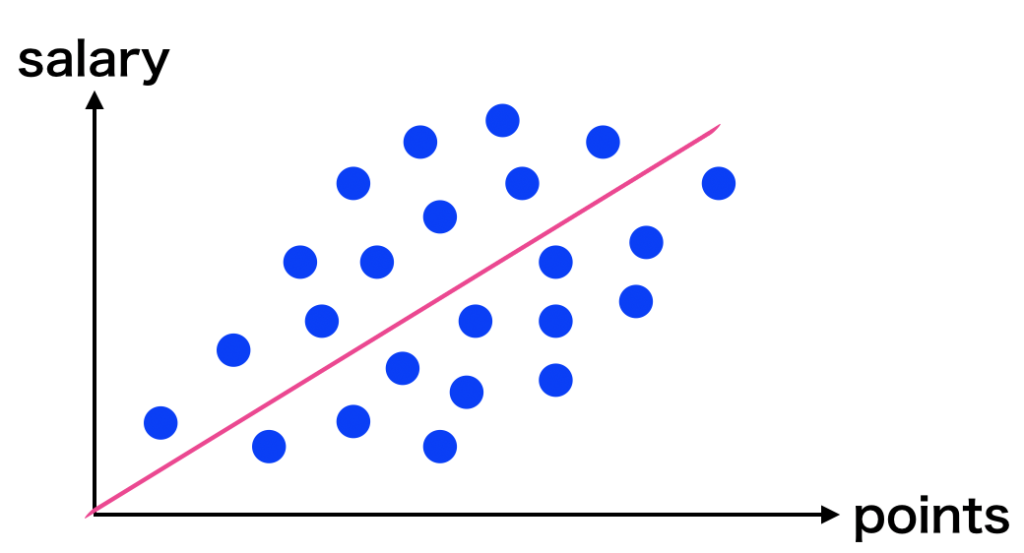
青点がデータ、赤色の実践が線形モデルで予測した値になります。人間の目で見ると、真ん中のモデルが最も適したモデルに見えますよね。
では実際にどの線形モデルが適切であるか、と言うことについて計算を用いて検証していきましょう。
損失関数を評価する(データとモデルとの距離)
N個あるデータのうち、$i$ 番目のデータ値 $\left(P_{i}, S_{i}\right)$ と線形モデル\(\hat{S}=a \times P+b\)との距離の最小値の求め方について考えていきましょう。
特に$i$ 番目の予測値\(\left(P_{i}, \hat{S}_{i}\right)\)と直線上の点である \(\left(P_{i}, S_{i}\right)\) の2点間の距離 \(d_{i}^{(1)}\) を求めます。
$ d_{i}^{(1)}=\left|S_{i}-\hat{S}_{i}\right|=\left|S_{i}-\left(a \times P_{i}+b\right)\right| \quad$
$(i=1, \ldots, N)$
※ 今後 \(d_{i}^{(2)}\) という距離も求めるため、今回は\(d_{i}^{(1)}\) という記載にしています。
損失関数を計算する(複数のデータ点と直線モデルとの距離)
散布図の複数のデータ点と線形モデルの距離を計算しましょう。
方法としては散布ずの各々のデータ点 \(\left(P_{i}, \hat{S}_{i}\right)\) と直線上の値 \(\left(P_{i}, S_{i}\right)\)との距離の平均値 \(\overline{d^{(1)}}\) を計算していく事とします。
\(\begin{aligned} \overline{d^{(1)}} &=\frac{d_{1}^{(1)}+d_{2}^{(1)}+\cdots+d_{N}^{(1)}}{N} \\ &=\frac{1}{N} \sum_{i=1}^{N} d_{i}^{(1)} \\ &=\frac{1}{N} \sum_{i=1}^{N}\left|S_{i}-\left(a \times P_{i}+b\right)\right| \end{aligned}\)
距離ベースで損失関数を評価をする
「散布図における多くのデータの点〜直線モデル上の予測値の距離」から作成した評価関数は以下の様になります。
$$D^{(1)}(a, b)=\frac{1}{N} \sum_{i=1}^{N}\left|S_{i}-\left(a \times P_{i}+b\right)\right|$$
この関数 \(D^{(1)}(a, b)\) にいろいろな $(a, b)$ を代入していき、最も小さい値になる $(a, b)$ の組み合わせを見つけることができれば「高精度な予測直線モデル」を決定することができます。
評価関数の性質
「評価関数 \(D^{(1)}(a, b)\) において $(a, b)$ のみが変数となる」と言うことが非常に重要なポイントです。
そのほかのデータに関わる値である\(S_{i}, P_{i}, N\) は、\(D^{(1)}(a, b)\) 定数というのも重要です。
すなわち \(D^{(1)}(a, b)\) は変数 \((a, b)\) のみによって変化する関数であると言えます。
このことについても以下の記事でまとめていますので、併せて読んで貰えれば理解が深まります。
» 単回帰分析と最小2乗法の求め方
ここで評価関数の特殊な特徴についておさえておきましょう。
評価関数に定数を足したり定数を引いたり、さらには定数倍しても、評価関数としての性質は変わらないということです。
そのため、自分が評価しやすい様に評価関数をアレンジすることが出来ます。
より実際的な距離ベースの評価関数:最小二乗法と損失関数
ここで評価関数を評価するために算出した距離ですが、距離 \(d_{i}^{(1)}\) を使用した評価関数 \(D^{(1)}(a, b)\) は、絶対値 \(\left|S_{i}-\hat{S}_{i}\right|\) で表します。
これでは数学的(解析的)に扱いづらくなってしまっています。理由は以下の記事に載せています。
» 単回帰分析と最小2乗法の求め方
そこで二乗距離を用いて評価関数をアレンジします。
すなわち、
$$d_{i}^{(2)}=\left(S_{i}-\hat{S}_{i}\right)^{2}=\left\{S_{i}-\left(a \times P_{i}-b\right)\right\}^{2}$$
を使います。この距離を使用する場合、評価関数は以下のように表現できます。
$$D^{(2)}(a, b)=\sum_{i=1}^{N}\left\{S_{i}-\left(a \times P_{i}-b\right)\right\}^{2}$$
以下のような表記をすることで、「\(D^{(2)}(a, b)\) を最小にするような $(a, b)$ の組み合わせが \(\left(a^{*}, b^{*}\right)\) である」と言えます。
$$\left(a^{*}, b^{*}\right)=\operatorname{argmin} D^{(2)}(a, b)$$
$argmin$ は「(右辺)を最小にするような引数(argument)の組み合わせ」という意味の演算子です。
このように二乗距離を最小にすることで最適解を求める方法を、最小二乗法と呼びます。
また「モデルとのズレ」を指標にした評価関数では「評価関数とモデルとのズレが大きいほど不適切なモデルである」という意味があり、評価関数のことを損失関数(コスト関数) (loss function, cost function) とも呼ばれます。
機械学習の文脈ではこちらの言い方のほうが多いので、以後はこの呼び方を多用します。
以後、この章では、\(D^{(2)}(a, b)\) を小さくする $(a, b)$ の組み合わせを考えていくことにします。
※ \(d_{i}^{(1)}>d_{j}^{(1)}\) なら、\(d_{i}^{(2)}>d_{j}^{(2)}\) であることを確認しましょう。
まとめ

最適化問題を評価関数を用いて解決する方法について解説していきました。
評価関数(損失関数)の最小2乗法によるモデルの最適化に必要な数式は理解しておくと、機械学習において非常に重要ですのでおさえておきましょう。
関連記事 【キカガク流】Udemyのキカガクを受講した感想【レビュー】
