こんにちは。産婦人科医のとみー(twitter:@obgyntommy)です。
この記事では具体的なワインのデータを用いて、機械学習のうち教師なし学習の一通りの流れを学びます。
特にこの記事では具体的な非構造化データを用いて教師なし機械学習(クラスタリング)の一通りの流れを学びます。
非構造化データは構造化データと同様の方法で次元削減を行うとクラスタリングがうまく行かないことが多く、今回はそれに対応できるような手法を学びます。
メモ
非構造化データとは、データサイエンスの分野で代表的なものは画像、文章、音声などのデータを指します。
逆に構造化データとはデータベースのテーブルにおさまるような顧客情報、ログのようなデータを示します。
今回学習する、機械学習のうち教師なし学習の一般的な流れは以下の通りです。
教師なし学習の機械学習の流れ
- データの内容の確認
- データの前処理
- Feature Scaling
- 次元削減
- 教師なし学習(クラスタリング)数の決定
- 教師なし学習(クラスタリング)
- 結果の解釈
Google Colaboratory でコードを動かす事も出来ますので、記事で学習するのが大変な方はこちらのリンクをご参照下さい。
scikit-learnを用いた機械学習の流れについては、以下の記事を参照して下さい。
-

【機械学習】scikit-learnの使い方【基礎から全て解説】
続きを見る
Google Colaboratoryの使い方については以下の記事を参照して下さい。
-

Google Colaboratoryの使い方【完全マニュアル】
続きを見る
尚、ワインのデータセットを用いた教師なしの機械学習についてはこちらの記事をご参照下さい。
-

【教師なし学習】機械学習でワインの品質判定を行ってみよう【scikit-learn】
続きを見る
それでは早速学習していきましょう。
データの読み込みとデータ内容の確認

skleanのライブラリから「MNIST」のデータセットを読み込みます。
MNISTのデータセットは典型的な画像データセットです。0から9の数字の白黒画像を表すデータとラベルがセットになっています。
今回はkerasのデータセットからMNISTのデータを読み込みます。
In[]
1 2 3 4 | import tensorflow as tf mnist = tf.keras.datasets.mnist (X_train_all, y_train_all),(X_test_all, y_test_all) = mnist.load_data() del mnist |
Out[]
1 2 | Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz 11493376/11490434 [==============================] - 0s 0us/step |
データ数を確認しましょう。
In[]
1 2 3 4 | print("X_train_all : ", X_train_all.shape) print("y_train_all : ", y_train_all.shape) print("X_test_all : ", X_test_all.shape) print("y_test_all : ", y_test_all.shape) |
Out[]
1 2 3 4 | X_train_all : (60000, 28, 28) y_train_all : (60000,) X_test_all : (10000, 28, 28) y_test_all : (10000,) |
(60000, 28, 28)とありますが、これはデータ数(画像数)が60,000、縦横が28*28の画像があるということになります。
それではデータの中身を確認しましょう。以下は、画像を表示しており、5という数字が表示されているのがわかると思います。
In[]
1 2 3 4 5 6 | import matplotlib.pyplot as plt %matplotlib inline plt.imshow(X_train_all[0], cmap='gray') plt.show() |
Out[]
データの前処理

今回はデータを全数使うと処理時間がかかってしまうため、データ数を削減します。
また、スケールを255に割ることでデータ値を0-1の間の値にします。
In[]
1 2 | X_train_255 = X_train_all[:20000].astype("float") X_train = X_train_255 / 255 |
次元削減

PCAによる次元削減
それでは次元削減を行います。まずは次元削減としては典型的なPCAを用いて次元削減を行ってみましょう。
基本的に次元削減をする際は、非構造データであればreshapeメソッドなどを活用し(データ数*特徴量)の形に直す必要があります。
In[]
1 2 | from sklearn.decomposition import PCA x = X_train.reshape(-1, 28*28) |
それでは、PCAで次元削減を行います。
fit_transform で学習と削減をいっぺんに行う事が出来ます。
In[]
1 2 3 | pca = PCA(n_components=2) arr_pca = pca.fit_transform(x) arr_pca |
Out[]
1 2 3 4 5 6 7 | array([[ 0.43248715, -1.28249664], [ 3.98927752, -1.43545064], [-0.14613026, 1.59220315], ..., [-2.57013999, -0.14291775], [-1.66233566, 1.0118905 ], [-1.46632527, -2.46825906]]) |
次元削減を行ったので、結果を可視化してみます。
2次元データへ削減しているので、2次元面にプロットしてみます。
In[]
1 2 3 4 5 6 | import seaborn as sns import pandas as pd plt.rcParams['figure.figsize'] = (20.0, 10.0) plt.rcParams['font.family'] = "serif" df_pca = pd.DataFrame(arr_pca,columns = ["pca_1","pca_2"]) sns.scatterplot( x='pca_1', y='pca_2',data=df_pca,palette="Set1") |
Out[]
1 2 3 | /usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm <matplotlib.axes._subplots.AxesSubplot at 0x7f2eb93172e8> |
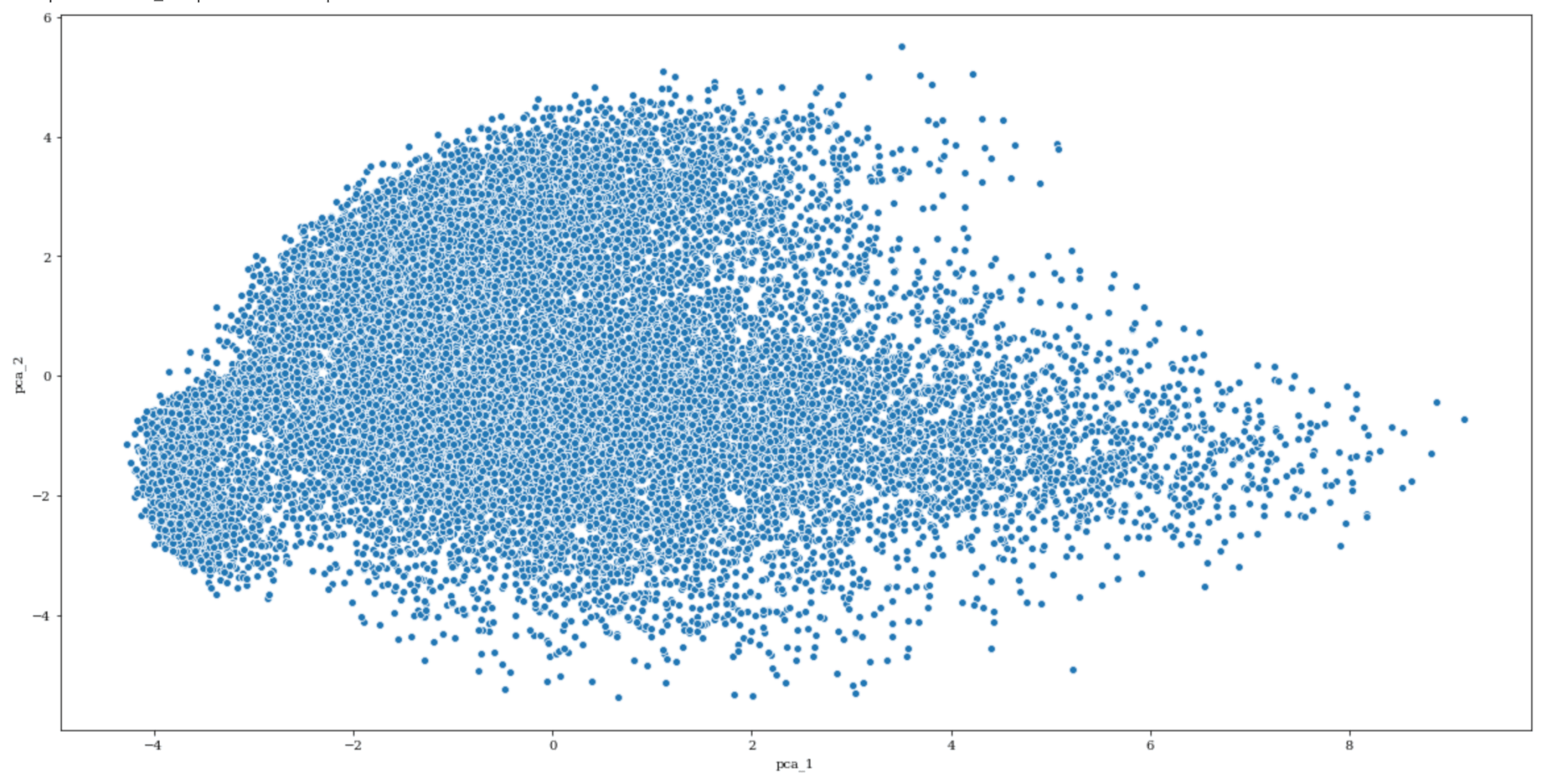
これからクラスタリングを行いたいところですが、上の結果を見るとあまりクラスタというクラスタは見当たりません。
PCAによる次元削減により情報削減が行われすぎて、それぞれのデータの特徴が消えてしまっているように見えます。
結論をいうと、つまり非構造データに対してPCAは有効でない場合が多いです。
PCAの次元削減の手法については本記事での解説は省略しますが、これはPCAの次元削減の方法が原因となります。
TSNEによる次元削減
次にTSNEという次元削減の手法を扱ってみます。
PCAのように fit_transform で次元削減が行えます。(ただしTSNEはモデルという概念がなく、fitのみでモデルの作成はできません。)
以下、処理になりますが5分くらい時間がかかります。珈琲の時間です。
In[]
1 2 | from sklearn.manifold import TSNE arr_tsne = TSNE(n_components=2, random_state=0, verbose=1).fit_transform(x) |
Out[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | [t-SNE] Computing 91 nearest neighbors... [t-SNE] Indexed 20000 samples in 2.795s... [t-SNE] Computed neighbors for 20000 samples in 715.486s... [t-SNE] Computed conditional probabilities for sample 1000 / 20000 [t-SNE] Computed conditional probabilities for sample 2000 / 20000 [t-SNE] Computed conditional probabilities for sample 3000 / 20000 [t-SNE] Computed conditional probabilities for sample 4000 / 20000 [t-SNE] Computed conditional probabilities for sample 5000 / 20000 [t-SNE] Computed conditional probabilities for sample 6000 / 20000 [t-SNE] Computed conditional probabilities for sample 7000 / 20000 [t-SNE] Computed conditional probabilities for sample 8000 / 20000 [t-SNE] Computed conditional probabilities for sample 9000 / 20000 [t-SNE] Computed conditional probabilities for sample 10000 / 20000 [t-SNE] Computed conditional probabilities for sample 11000 / 20000 [t-SNE] Computed conditional probabilities for sample 12000 / 20000 [t-SNE] Computed conditional probabilities for sample 13000 / 20000 [t-SNE] Computed conditional probabilities for sample 14000 / 20000 [t-SNE] Computed conditional probabilities for sample 15000 / 20000 [t-SNE] Computed conditional probabilities for sample 16000 / 20000 [t-SNE] Computed conditional probabilities for sample 17000 / 20000 [t-SNE] Computed conditional probabilities for sample 18000 / 20000 [t-SNE] Computed conditional probabilities for sample 19000 / 20000 [t-SNE] Computed conditional probabilities for sample 20000 / 20000 [t-SNE] Mean sigma: 1.886709 [t-SNE] KL divergence after 250 iterations with early exaggeration: 91.979645 [t-SNE] KL divergence after 1000 iterations: 2.176347 |
処理が終わりましたので、結果を可視化してみましょう。
In[]
1 2 | df_tsne = pd.DataFrame(arr_tsne,columns = ["tsne_1","tsne_2"]) sns.scatterplot( x='tsne_1', y='tsne_2',data=df_tsne,palette="Set1") |
Out[]
1 | <matplotlib.axes._subplots.AxesSubplot at 0x7efdd3a8aef0> |
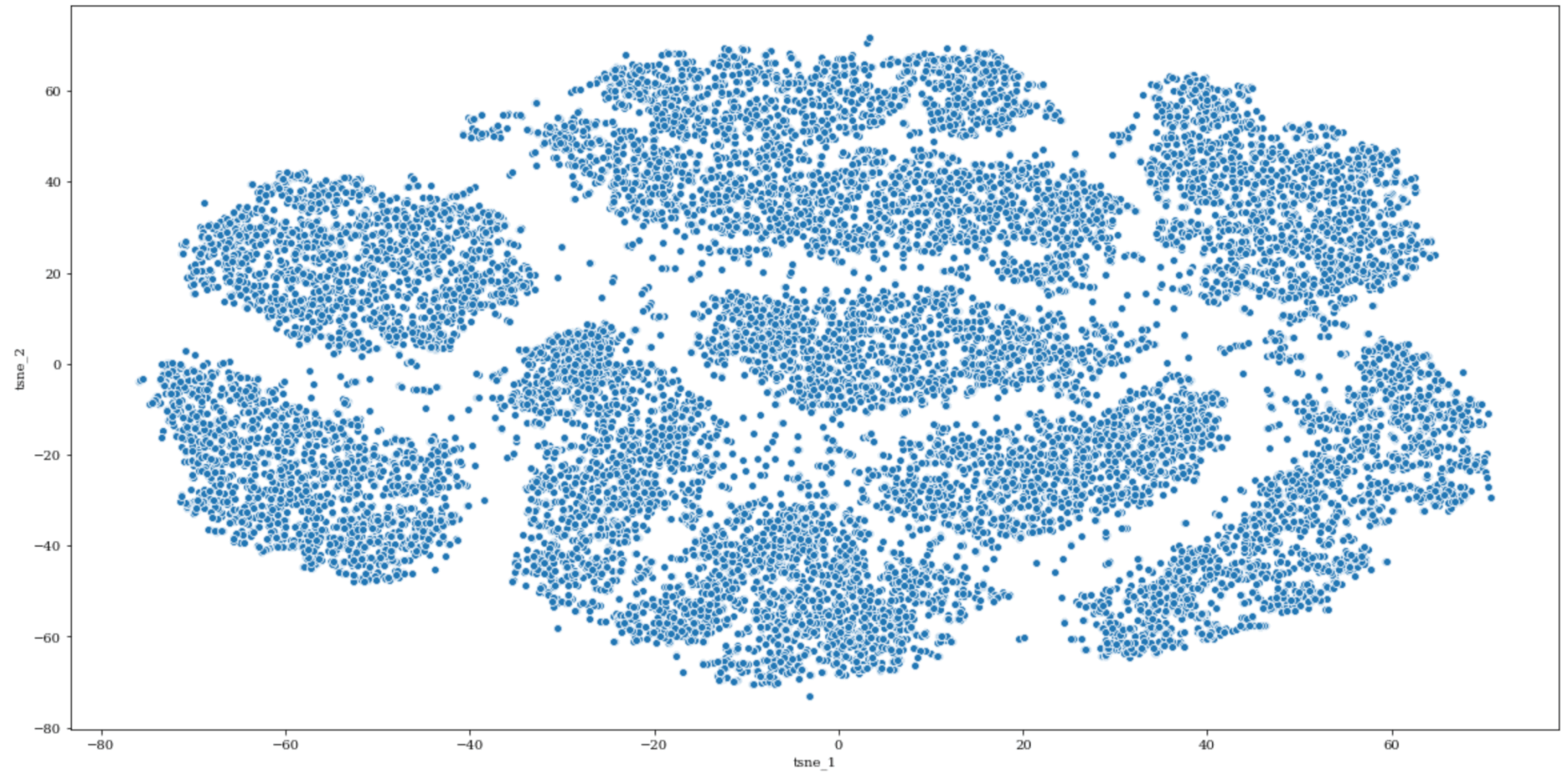
これを見ると、PCAの時とは違いクラスタのようなものが現れているのがわかります。
それではこれからクラスタリングに入っていきます。
教師なし学習(クラスタリング)

クラスタリングというと一般的にK-meansが有名ですが、K-meansはクラスタの形状として真円を前提とするため、非構造データの際はクラスタの形状を事前に確認しておく必要があります。
k-meansについては以下のYouTube動画が分かりやすいので参考にどうぞ。
形状を確認すると、円だけではなく長細い形状のクラスタも確認できます。
よってK-meansだとうまくクラスタリングできない可能性がありそうです。
このような時は『DBscan』というクラスタリング手法が有効な場合があります。
DBscanは簡単にいうと密度を元にしたクラスタリング手法であり、クラスタがどんな形であれデータが密集しているとそれをクラスタとみなします。
DBscanについても英語ですが、分かりやすいYouTubeがあったので参考にして下さい。
それではDBscanによりクラスタリングを行います。DBscanはsklearnに含まれています。
ハイパーパラメータとしては eps,min_samples がありますが、これは『あるデータ点の距離eps内に他のデータポイントが min_samples 個以上存在するか』を全てのデータ点に対して計算し、クラスタの構成点を判断します。
今回はハイパーパラメータ探索は目視により行いましたので、あらかじめ設定してあります。
In[]
1 2 3 4 | from sklearn.cluster import DBSCAN db = DBSCAN(eps=1.4, min_samples=5) labels = db.fit_predict(arr_tsne) df_tsne["label"] = labels |
それでは、クラスタリングの結果とデータ点を可視化してみましょう。
In[]
1 | sns.scatterplot( x='tsne_1', y='tsne_2',data=df_tsne, hue="label",palette="Set1") |
Out[]
1 | <matplotlib.axes._subplots.AxesSubplot at 0x7efdd2d96748> |
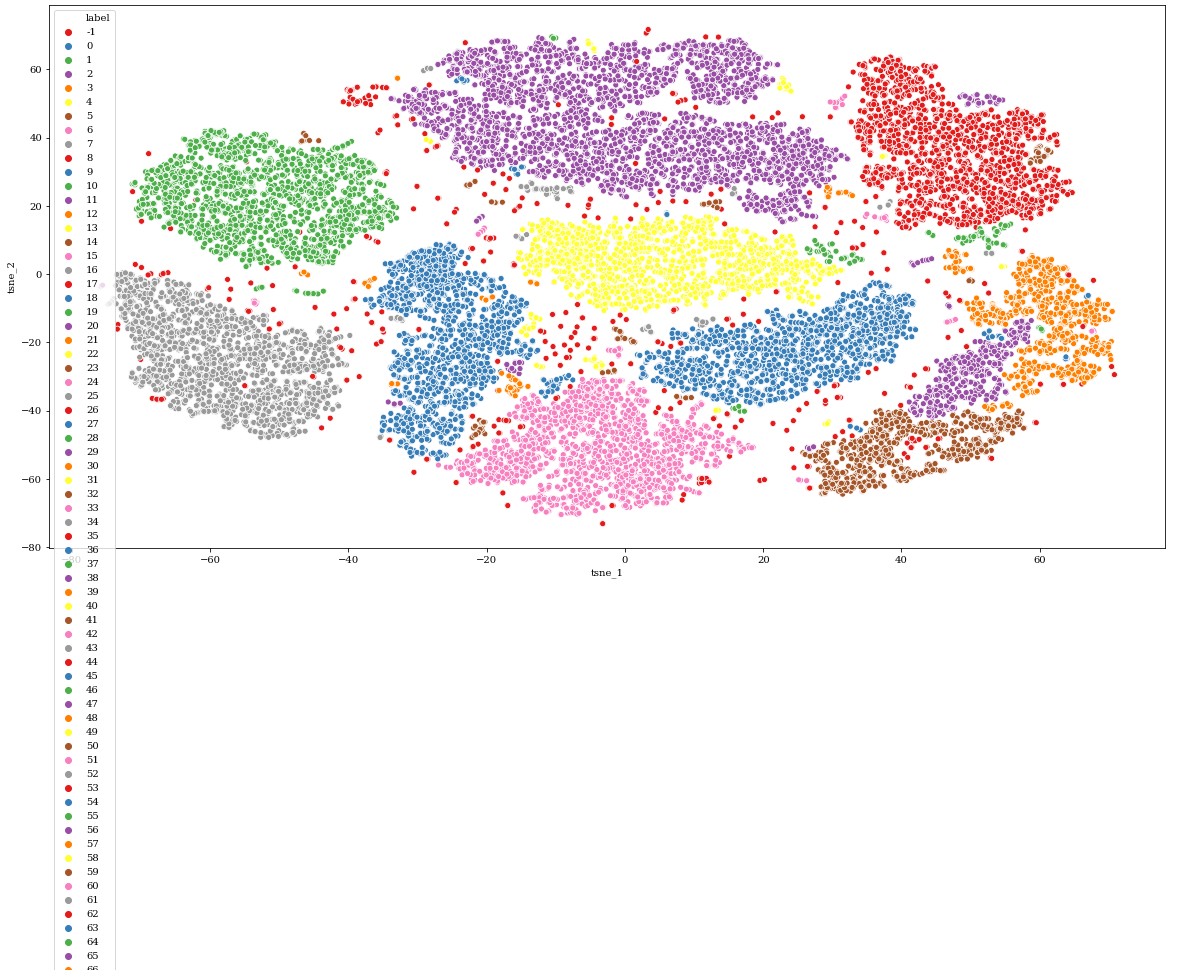
※ 一部省略しています。
クラスタリング結果の解釈

クラスタリングの結果を考察しますが、ここではシンプルにクラスタ毎のデータ画像を確認してみて、それが妥当かを定性的に判断してみましょう。
うまくクラスタリングできているところもありますが、一部クラスタに含まれていないデータ点が存在します。
一旦これらは考慮せず、クラスタになっているデータのみを抜き出してみます。
In[]
1 2 3 | df_tsne_main_group = df_tsne[df_tsne["label"].isin([0,1,2,3,4,5,6,7,8,9])] arr_main_group = X_train_255[df_tsne_main_group.index,:,:] sns.scatterplot( x='tsne_1', y='tsne_2',data=df_tsne_main_group, hue="label",palette="Set1") |
Out[]
1 | <matplotlib.axes._subplots.AxesSubplot at 0x7f9c9a929cc0> |
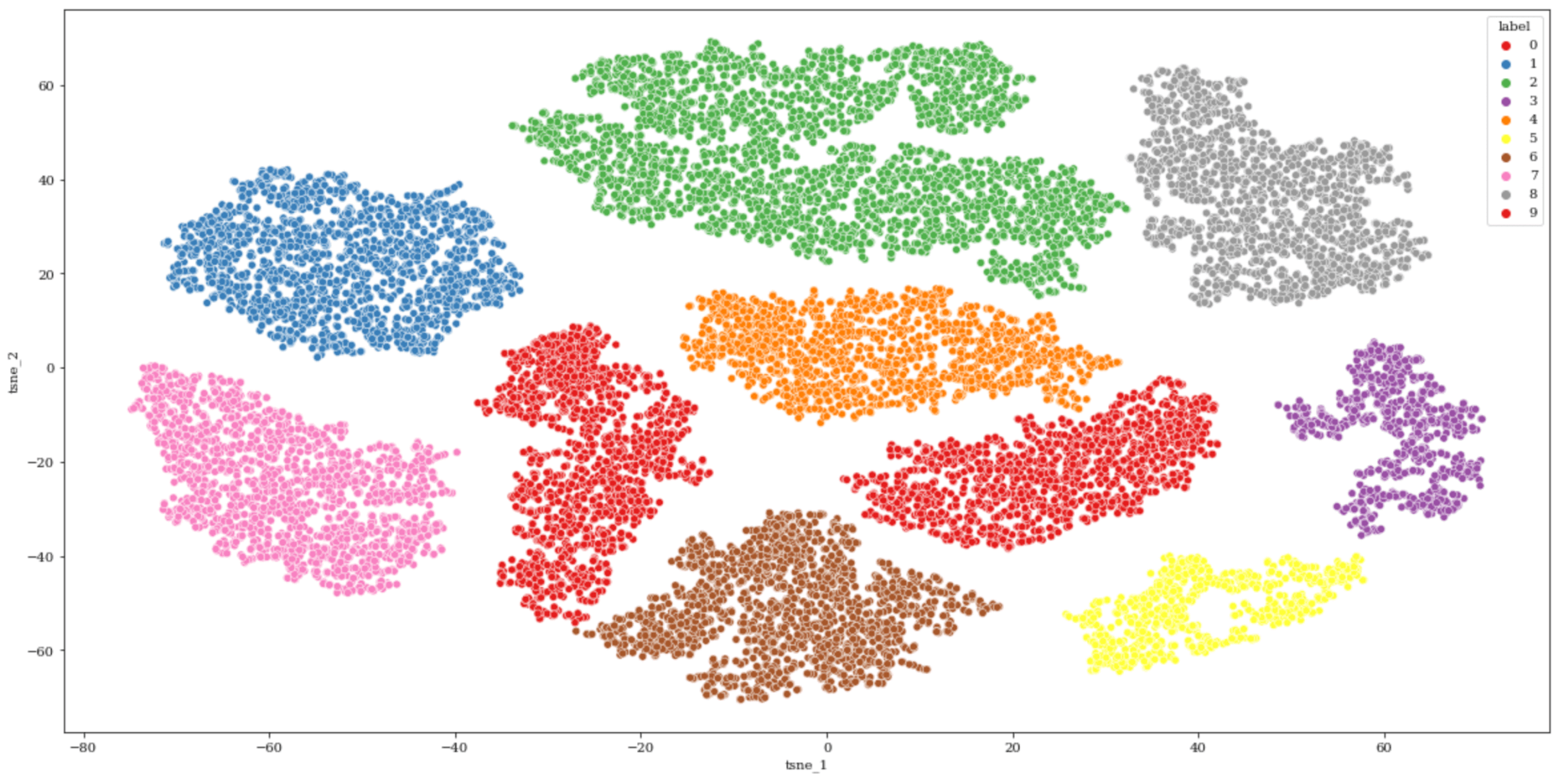
うまい具合にクラスタに分けられました。それではそれぞれのクラスタの画像を5枚づつ表示してみましょう。
※ 画像表示の部分にあるCluster No. の数字は画像内の数字とは関係はな胃です。
In[]
1 2 3 4 5 6 7 8 9 10 11 | df_label = df_tsne_main_group.groupby("label").apply(lambda x:x.head().reset_index())["index"].reset_index() df_label.head() plt.rcParams['figure.figsize'] = (2.0, 2.0) def show_pic(x,arr): index = x["index"] label = x["label"] print("Cluster No. :",label) plt.imshow(arr[index], cmap='gray') plt.show() df_label.apply(lambda x:show_pic(x,X_train_255),axis=1) |
Out[]
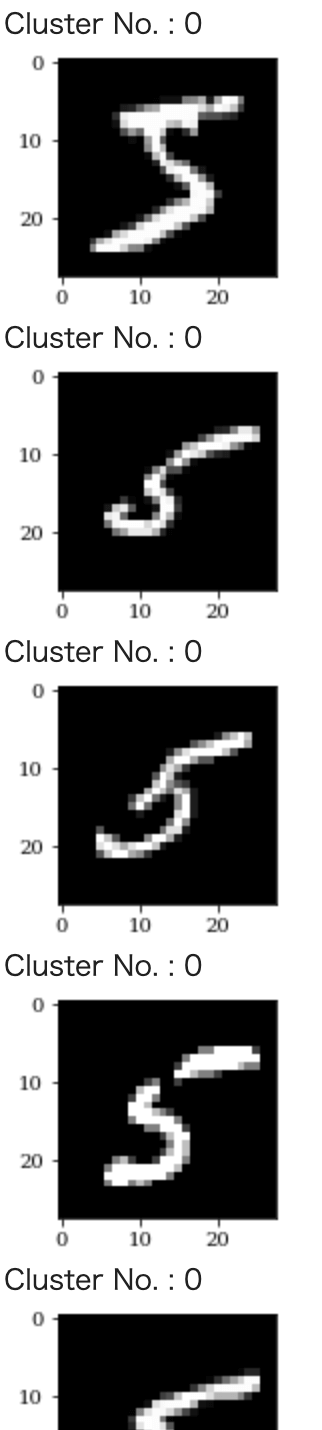
※ 出力結果は全て表示していません。
さて、それぞれのクラスタの結果を定性的に確認してみましょう。
大部分はそれぞれのCluster No. ごとに同じ数字の画像になっていると思います。
これは画像のような非構造化データでもTSNEによりうまくデータの特徴を捉え、クラスタに分類できていることを意味しています。
ただし、同じクラスタ内に4,9、もしくは1,7など複数含まれていることがあります。
これは人間が見ればなんとなく違うとわかりますが、確かに画像としては似通っています。これは逆に『紛らわしい文字』であると判断できます。
TSNEによるクラスタリングにより、ラベルがついていないデータの大まかな分類や『紛らわしさがある』データの抽出が可能です。
本チュートリアルはここで終了しますが、どなたか先ほどの処理で除外したクラスタ外のデータを逆に使って『紛らわしいデータ』の抽出と考察を行って頂けると幸いです。
面白いと思いますが、今の僕には余力がないので、どなたかお願いします。今回は以上となります。
再度Google Colaboratoryで学習する際には、以下からどうぞ。
-
Google Colab
続きを見る
