ガウス分布【正規分布】とは

統計学の勉強をしたい人

正規分布、ガウス分布について基本から詳しく知りたい。

分布が表す数式や、3σ法についても具体的に知りたい。

この様な方に向けての記事になります。

この記事では正規分布について解説していきます。

正規分布（normal distribution）は正式には「標準正規分布」と呼ばれ、ガウス分布（Gaussian distribution）とも呼ばれることがあります。

グラフの図表としては以下の様な式になります。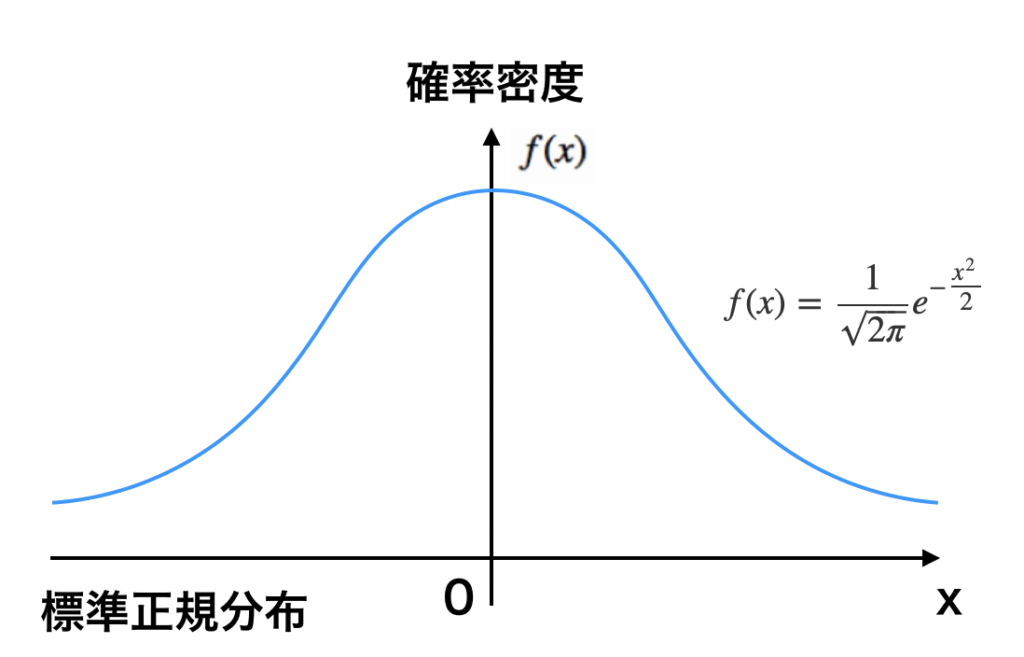
標準分布、または標準正規分布、またはガウス分布のグラフ
この分布の特徴としては平均が 0、標準偏差が 1 になるという特徴があります。

これを $N(0, 1)$ と表現されます。

正規分布（ガウス分布）の確率密度関数は，後ほど再度紹介しますが、

$$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left\{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right\}$$

この様な式になります。

ではこの正規分布についてより詳しく見ていきましょう。

標準正規分布【ガウス分布】とは

正規分布（ガウス分布）とは，図のような左右対称の連続型の確率分布です。

正確な定義（確率密度関数）については次の項で説明します。

正規分布は分布の中でも代表的な分布のうちの一つです。

この記事では，正規分布について，確率密度関数の式の意味の理解を中心に解説します。

正規分布の確率密度関数について解説します。

正規分布（ガウス分布）の確率密度関数は，

$$f(x)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left\{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right\}$$

です。

平均は $\mu$ , 分散は $\sigma^{2}$ です。

すなわち、N( $\mu$, $\sigma^{2}$ ) と表せます。

正規分布の確率密度関数は複雑そうですが，正規分布の中でも平均が $\mu=0$ 分散が $\sigma^{2}=1$ であるようなものが標準正規分布と呼ばれます。

この標準正規分布が基本形となるので押さえておきましょう。

標準正規分布の確率密度関数は $f(x)=\frac{1}{\sqrt{2 \pi}} e^{-\frac{x^{2}}{2}}$ です。だいぶ簡単になりましたね。

標準正規分布のグラフは下図のようになります。例えば 0 以上 a 以下となる確率は斜線部分の面積になります。

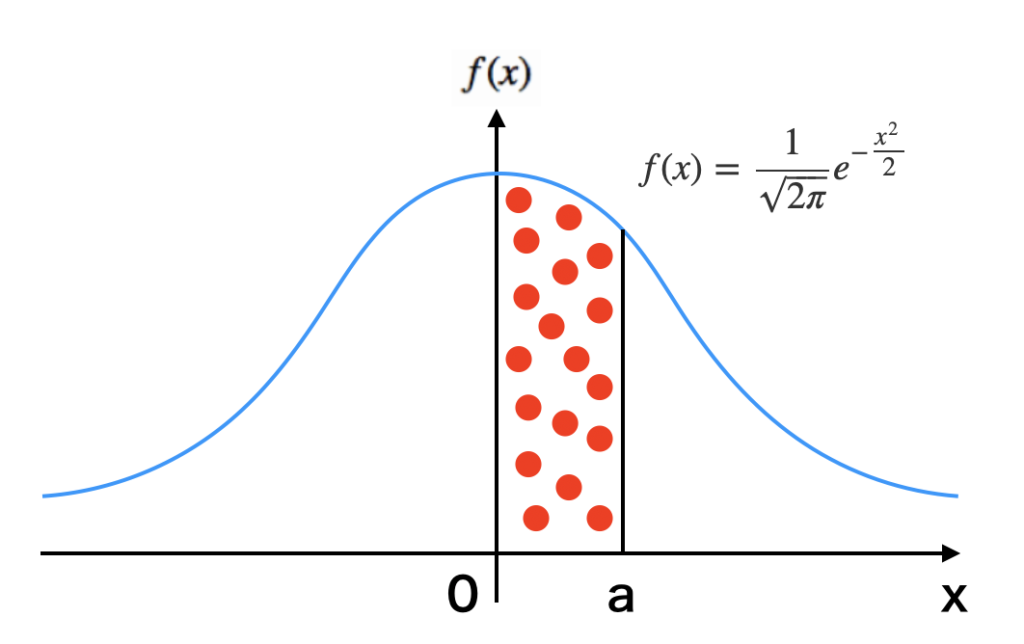
標準正規分布のグラフのうち、0 以上 a 以下となる確率は赤点で示した箇所の面積になります。

なお，指数関数 $e^{A}$ において $A$ が複雑な式のとき書きづらいので $\exp (A)$ $\exp (A)$ と書いています。

正規分布においてσ=1 の場合を考えてみましょう。

$[-\sigma, \sigma]$ を「1シグマ $(1 \sigma)$ 区間」と言います。

以下の図に1σ区間の面積を赤点で示しています。

この赤点の部分の面積が約68%になる訳です。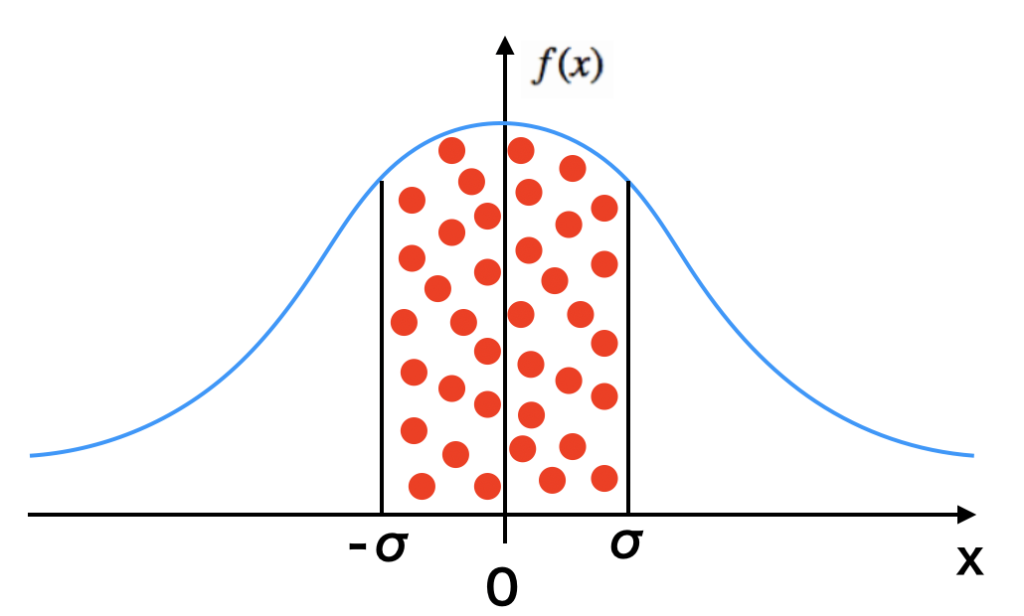
標準分布、または標準正規分布、またはガウス分布のグラフ
同様に，$[-k \sigma, k \sigma]$ を「 $k$ σ区間」と言います。

σ=2 の場合だと、2σ区間に入る確率は約95％になります。

3σ区間に入る確率は約99.7％です。ここでわかるのが、「2σを超える分布に属するデータはほとんどない」ということがわかります。

この記事では、ガウス分布【正規分布】の基本形について学びました。

　正規分布の特徴

さらに追加すると

ここからわかるのは、正規分布（ガウス分布）は真ん中が非常に多く密集していて端に行くほどデータがほぼない様な分布になるんだな、ということを理解しましょう。