【機械学習に必要な確率の基礎】事象、同時確率、条件付き確率

統計学を学びたい人

確率の基礎となる、事象、同時確率、条件付き確率についてまなびたいなぁ

この記事では確率の基礎概念の復習をします。

「これから、機械学習やディープラーニングの学習をしたいけど、その過程で数学、特に確率で挫折してしまった」という方に向けです。

　本記事の学習内容

今回の内容は基本的な内容ですが、記事を読み進むに連れて、「ベイズ統計学」が系統的に学習できる流れになっています。

確率の中では非常に基本的な内容となっているため、確率の基礎をわかっている方やAI・機械学習・プログラミングに興味のない方はスルーしてください。

では早速見ていきましょう。

機械学習に向けての確率の基本事項

ここで、サイコロを例にとって解説していきます。

サイコロを振る際に、サイコロで 3 の目が出る確率は以下の式で表すことができます。

$$ p(X=3)=1/6 $$

ここで、この式で出てくる文字の意味を覚えておきましょう。

まずは、この言葉の定義をおさえておいてください。

さらに、「確率変数」という言葉もおさえておきましょう。

確率変数とは、ある変数の値をとる確率が存在する変数のことです。

サイコロを振るたびに出る目が異なるのは確率によるわけです。

そのため、このサイコロの出る目(1,2,3,4,5,6 のうちのどれか)が出る確率のことを「確率変数」と言います。

そこで、サイコロを振った時に出る目の確率変数は以下の様に表すことができます。

確率変数 RVS：{1, 2, 3, 4, 5, 6}

RVS は Random Variables の略です。Pythonを使用する際にも出てくる用語ですので、覚えておきましょう。

また、サイコロを振った際に1〜6の目それぞれが出ることを全事象と言い、例えば1のみの目が出ることを事象と言います。

丁度、下の図を参考にしてください。

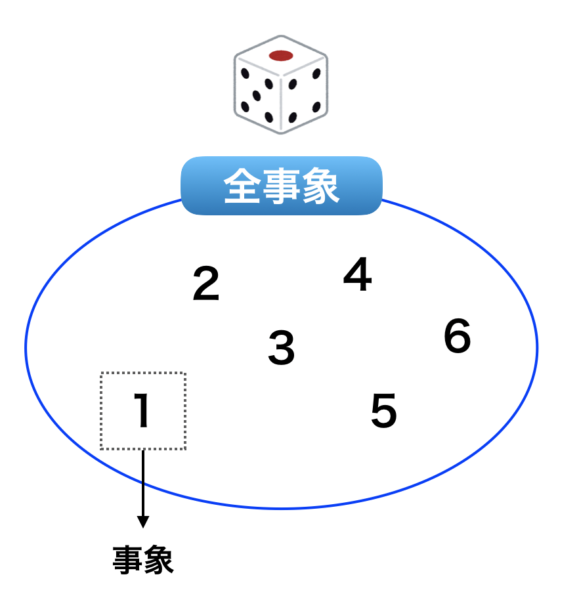
確率分布

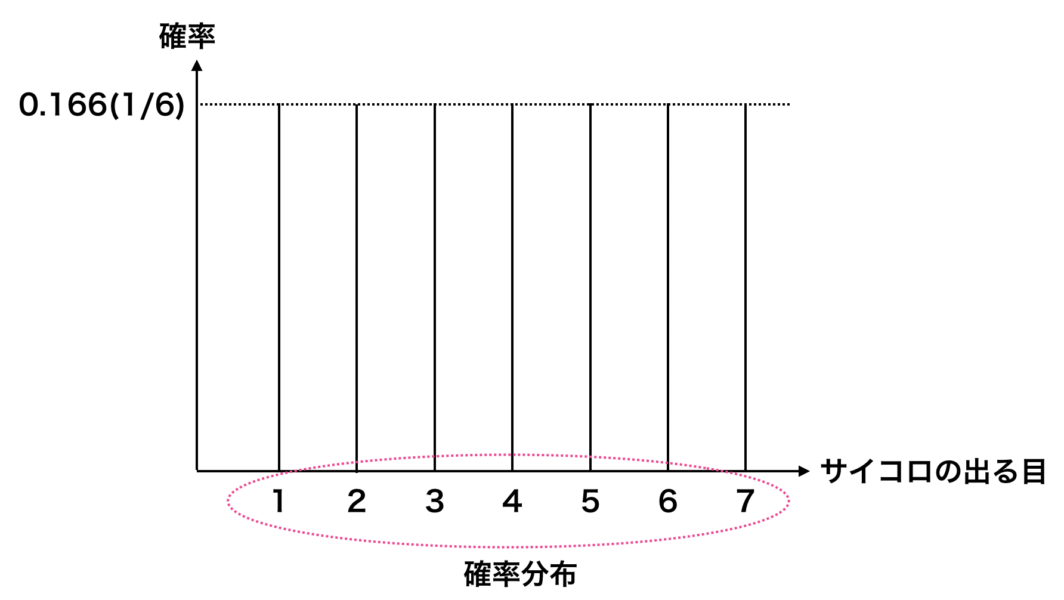
確率分布とは確率変数($X$)の確率の分布のことです。

確率変数 $X$ がどの値を取りやすいのかを視覚的に把握できるという点で有用です。

例えばサイコロの出る目の確率分布は丁度上の図の様になります。

確率質量関数と確率密度関数

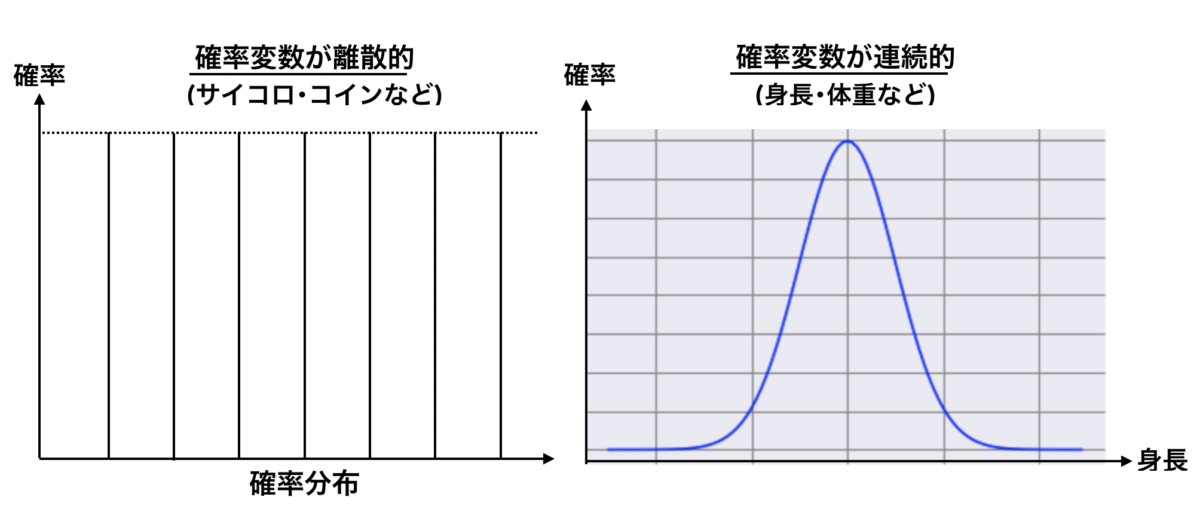
分布は離散的なものと連続的なものに分類することができます。

例えばサイコロの目が1, 2, 3が出る確率は $1/6$ と飛び飛びになってしまいます。

この飛び飛びの確率のことを「確率変数が離散的」と表現します。

身長や年収に関わってくる様などの値も取りうるものに関しては、連続した確率の値が出ます。

この様な確率の値が連続しているもののことを「確率変数が連続的」と表現します。

各々に関して数式で表現することが出来、以下の様な表現方法となります。

この2つの言葉をおさえておきましょう。

積事象、和事象、余事象について

積事象について

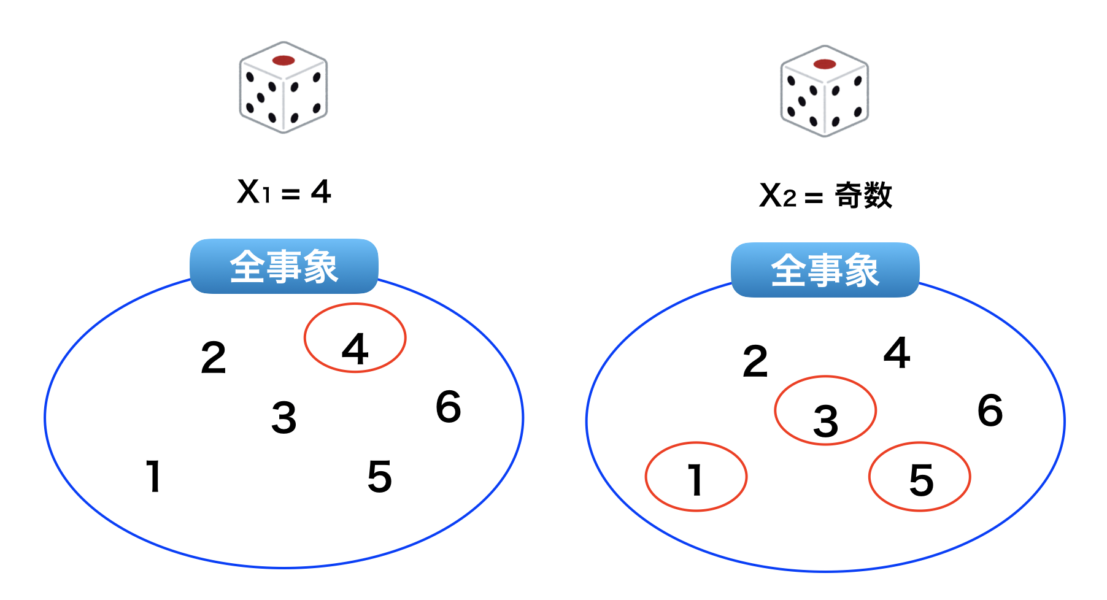
サイコロを例に取って考えてみると、1回目にサイコロの4が出て、2回目にサイコロの目が奇数となる確率は

• $X_1$ 1回目にサイコロの目が3である確率
• $X_2$ 2回目にサイコロの目が偶数の確率

すなわち、「1回目にサイコロの4が出て、2回目にサイコロの目が奇数となる確率」はそれぞれが独立した事象のため、掛け算を行います。

$p(X_1=4) p(X_2=奇数) = 1/6 ×1/2$ となります。

和事象

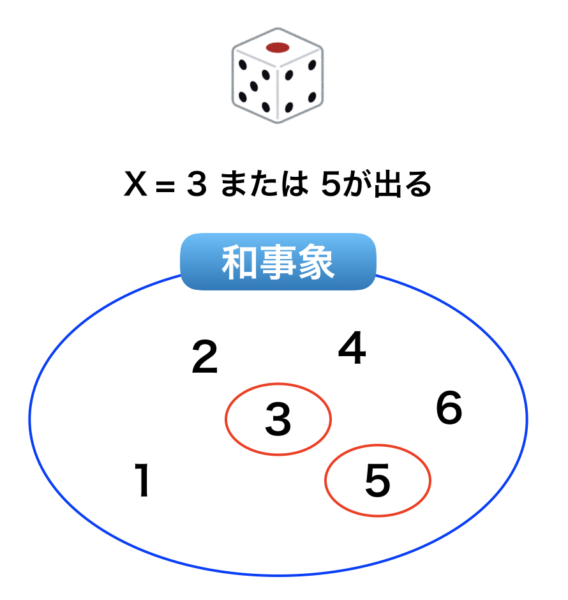
サイコロの目が 3 または 5 が出るときの確率です。

$p(X=3\cup 5)$ は 3 または 5 の目が出る確率を表現します。

また各々の事象は排反する事象のため $p(X=1)+p(X=2)$と表現します。

$$ p(X=3\cup 5)=p(X=1)+p(X=2) $$

余事象

サイコロで5以外が出る確率。

$p(X=1,2,3,4,6) $ 5以外が出る確率はこの様に表されます。

$$ p(X=1,2,3,4,6)=1.0 - p(5) $$

確率の総和は必ず 1.0 のため、理解できますよね。

同時確率と条件付き確率について

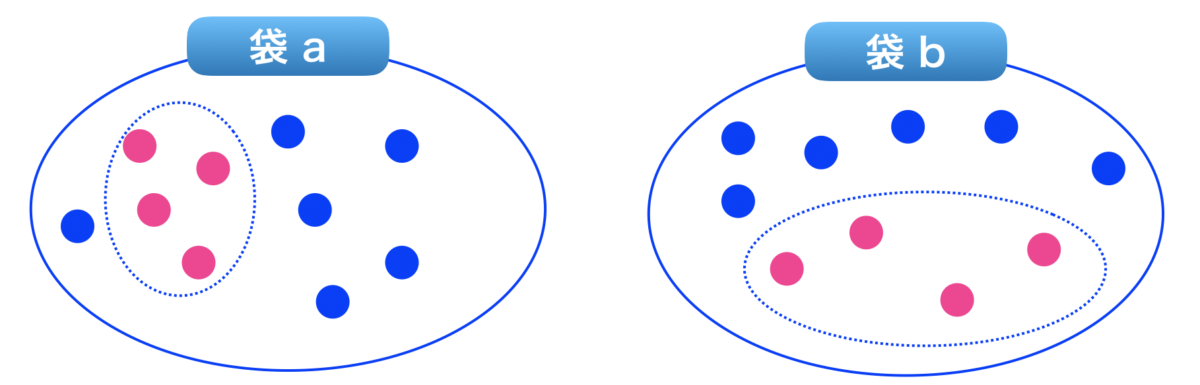
同時確率について

ここで2種類の箱があるとします。

各々につき10個ずつ玉が入っていて、袋aのうち 4個が赤玉、袋bのうち 4個が赤玉とします。

「袋が a で赤玉を引く確率」のことを同時確率と言います。

「袋が a で赤玉を引く確率」は以下の様な式で表す事ができます。

$$ p(X=a, Y=r) = p(Y=r|X=a)p(X=a) $$

$p(X=a, Y=r)$ とは「袋aを選択して赤玉を引く確率」のことです。

この2つの事象が同時に起こることを同時確率と言います。

$p(Y=r|X=a)$ とは「袋aが選ばれた上で、赤玉を引く確率」のことです。

この右辺が条件のもとで、左辺が起こる確率のことを条件付き確率と言います。

$p(X=a) $ とは「袋 a を選択する確率」のことです。

ちなみに袋 a と b は同じ確率で引くこととします。

具体的に計算すると

となります。

独立事象

独立事象とは、「袋から赤玉を引きつつ、別の場所でサイコロを振っていたところ3の目が出る。」という事象です。

袋 a を選んだ上で3が出る確率を求めてみましょう。

X：袋の選択
Y：サイコロの目で3が出る確率

とします。

ここで、以下の式を理解しましょう。

$$p(X=a, Y=3)$$

左側が袋 a を選ぶと言う事を意味します。

右側は3が出ると言う事を意味します。

これら2つの事象の間には相関性はなく、お互いに独立しているために「独立事象」と言います。

すなわち各々の確率の積として表現することができます。

$$ p(X=a, Y=3) = p(X=a)p(Y=3) $$

この式が「袋aを選んだ上で3が出る確率を表す式」となります。

周辺化

周辺確率について説明します。

ここで再度袋についてたとえます。

まず袋のAかBについて各々1/2の確率で選びます。

そして選ばれた時点で、1個の球を選択します。そこで赤玉が出る確率のことを「周辺確率」と言います。

この2つの確率の総和が「求めるべき確率」となります。これを「周辺確率」と言います。

以下の式を確認しましょう。

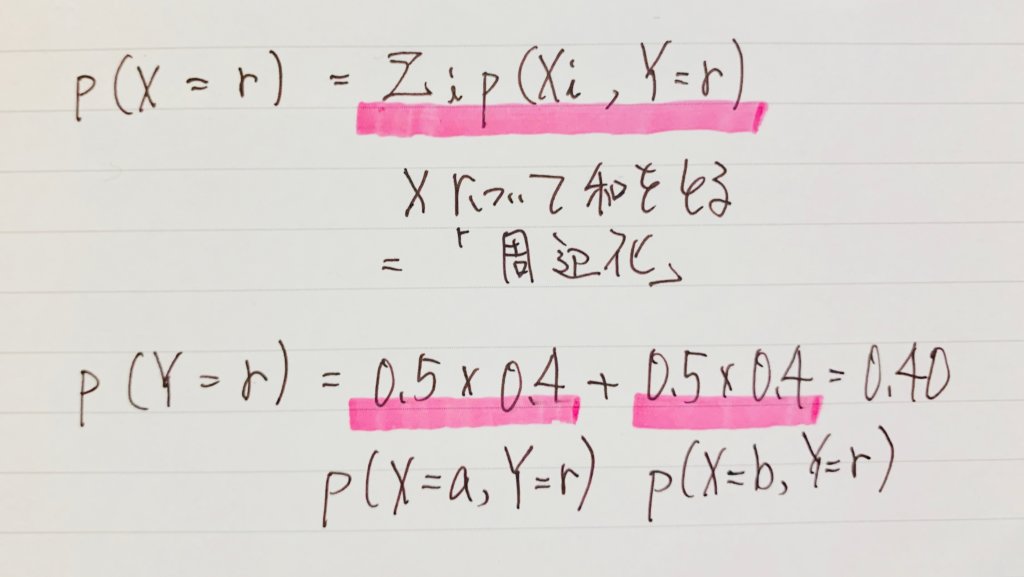
この様に2つの確率の和を取ることを周辺化と言います。（手書きでスミマセンm(_ _)m）

$0.5×0.4$ は $p(X=a, Y=r)$ すなわち、袋aを選んだ上で赤玉を取り出す確率

$0.5×0.4$は $p(X=b, Y=r)$ すなわち、袋bを選んで赤玉を取り出す確率

となります。

まとめ：機械学習には確率が必要不可欠

如何でしたでしょうか。

確率変数、事象、確率分布など基礎的な用語を説明しました。

確率変数は離散的なものと連続的なものがあります。

同時確率と条件付き確率、独立事象、周辺確率についても学習しました。

ここまで読んでいただければ、各々の場合についての簡単な計算はできる様になったはずです。

ここまでの記事を呼んで頂いた方は以上が最低限身についたかと思います。

次回は確率の【平均値・分散】について簡単に解説していきます。

是非一緒に頑張りましょう。