
この記事では「機械学習に必要な確率の基礎【事象、同時確率、条件付き確率】」に引き続き、確率の基礎概念のまとめを行います。
-

【機械学習に必要な確率の基礎】事象、同時確率、条件付き確率
続きを見る
「これから、機械学習やディープラーニングの学習をしたいけど、その過程で数学、特に確率を勉強する過程で挫折してしまった。」という方に向けた記事になります。
本記事での学習内容
- 期待値・分散とは
- 期待値・分散の定義
- 期待値・分散の性質
- 期待値・分散の公式一覧の把握
統計学の基礎的な知識である、期待値や分散の復習を行います。
確率の中では非常に基本的な内容となっているため、確率の基礎を理解している方や、AI・機械学習・プログラミングに興味のない方はスルーして頂く様にお願い致します。
では早速見ていきましょう。
機械学習に向けての確率の基本事項②

この項での学習目標は以下の2点です。
この項での学習内容
- その1:期待値・分散の定義と計算方法が理解できる
- その2:期待値・分散の数学的な性質・性格がわかる。
特にこのセクションでは期待値や分散に関するイメージをつかむことが重要です。
期待値・分散とは
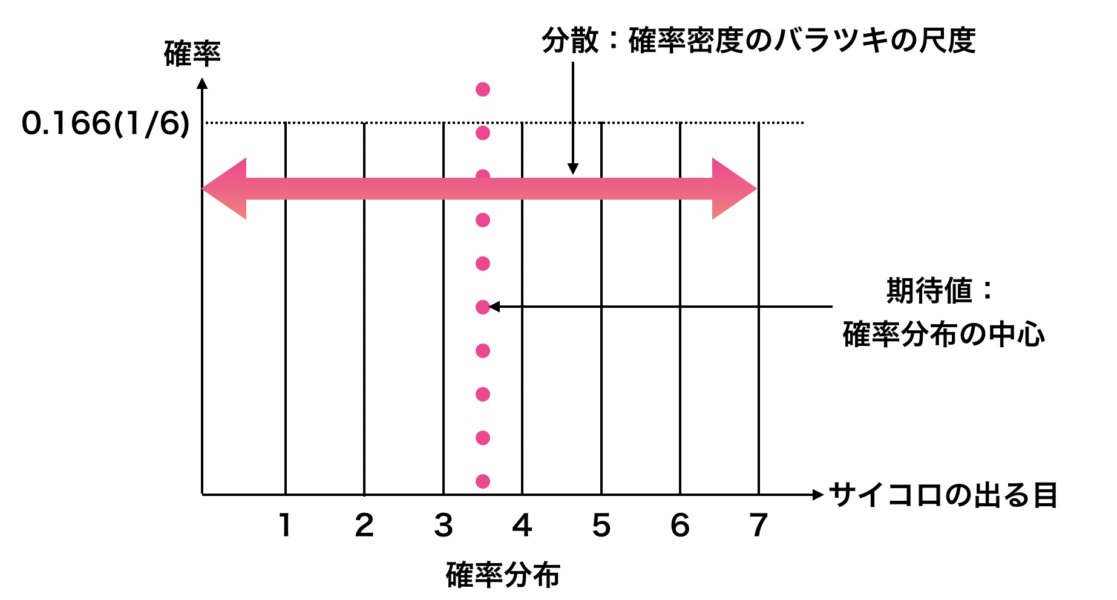
期待値と分散の違い
分散とは「確率分布のバラツキの尺度」のことを言い、期待値とは「確率分布の重心」のことを言います。
これら2つともに確率分布を特徴付けるパラメーターとなります。
例えば、サイコロを降るたびに目の値が違いますよね。そのバラツキ具合を調べる際に「分散」を用います。
- 分散:バラツキの尺度
- 期待値:分布の重心
とおさえておきましょう。
期待値の意味
「仮に1万個のサイコロを同時に投げた時に、その平均値は?」という問題があったとします。
N個のサイコロの目のバラツキは期待値を中心として周りに散らばっている、ということが分かります。
このN個が100個よりも1000個、10000個と増えれば増えるほど平均値は期待値に近づいていくわけです。
赤は1000個の場合、青は5000個の場合です。
これは、" 多数の系の平均は期待値に近づいていく " といえます。
これこそが、期待値の意味(= 中心極限定理)です。
期待値の定義
$$E[X]=\sum_{x} x p(x)$$
期待値の定義の式をおさえておきましょう。定義の式の各パーツについて説明します。
- $E[X]$ :$X$ の期待値
- $x$ :値
- $p(x)$ :確率
$E$ は'Expected value'の頭文字の $E$ から来ています。
左辺 $E[X]$ は " $X$ の期待値" を意味しており、右辺 $\sum_{x} x p(x)$ は例えばサイコロのでた目の「値」とサイコロの目が出る確率を表しています。
※ 連続変数の場合にはインテグラルを仕様する場合もあります。
ここでサイコロの出る目の期待値を算出してみましょう。
以下の式になるはずです。
\cdots+6 \times \frac{1}{6} $$
$$ =3.5$$
分散の定義
$$V[X]=\sum_{x}(x-E[X])^{2} p(x)$$
上の式が分散の定義となります。
- $V[X]$ は $X$ の分散を表します。$V$ は分散の意味である "Variance" に由来します。
- $x-E[X]$ は期待値との差を表します。
- $p(x)$ は確率を表します。
特に右の辺 $\sum_{x}(x-E[X])^{2} p(x)$ は、サイコロを例えに使用すると、"実際にサイコロの出た目の値"と"サイコロの目が出る期待値"の差と、「サイコロの目が出る確率の積」 となります。
※ 連続変数の場合にはインテグラルを使用します。
ここで、サイコロの目が出る分散を求めてみましょう。以下の式の様になるはずです。
$V[X]=(1-3.5)^{2} \times \frac{1}{6}+(2-3.5)^{2} \times \frac{1}{6}+$
$+\cdots+(6-3.5)^{2} \times \frac{1}{6}=\frac{35}{12}$
期待値と分散の性質
ここからは式の紹介となります。
少々式をみるだけで吐き気を催すかもしれませんが、覚えておきましょう。
期待値の性質①:公式一覧
① $E[c X]=c E[X]$
② $E[c]=c$
③ $E[X+Y]=E[X]+E[Y]$
④ $E[X Y]=E[X] E[Y]$ ($X$ と$Y$ が独立である時)
- $E[c X]=\sum_{x} c x p(x)=c \sum_{x} x p(x)$
- $E[c]=\sum_{x} c p(x)=c \sum_{x} p(x)$ この右辺は「確率の総和が1であることを示しています。」
- $E[X+Y]=\sum_{x} \sum_{y}(x+y) p(x, y)=$
$=\sum_{x} \sum_{y} x p(x, y)+\sum_{x} \sum_{y} y p(x, y)$ - $E[X Y]=\sum_{x} \sum_{y} x y p(x, y)=$
$=\sum_{x} x p(x) \sum_{y} y p(y)$
以上が、期待値の公式となります。
これらの式は式変形を用いるので少々難しく感じるかもしれませんが、それほど難しくない様ですので、手を動かしてみてみてください。
分散の性質①:公式一覧
$X$ と$Y$ が独立していると仮定します。
$$ V[X+Y]=V[X]+V[Y] $$
$ V[X+Y]=$
$=\sum \sum((x+y)-E[X+Y])^{2} p(x, y) $
すなわち
$V[X+Y]=$
$=\sum_{x} \sum_{y}((x-E[X])+(y-E[Y]))^{2} p(x, y)$
$x-E[X]=A$, $y-E[Y]=B$, とおき、お互いが独立していることを用いると
$V[X+Y]=$
$=\sum_{x} \sum_{y}\left(A^{2}+2 A B+B^{2}\right) p(x) p(y)$
$\sum \sum((x+y)-E[X+Y])^{2} p(x, y)$ この項を変形すると
$\sum_{x} \sum_{y}(x-E[X])(y-E[Y]) p(x) p(y)$ となります。
さらに、
$\sum_{x}(x-E[X]) p(x) \sum_{y}(y-E[Y]) p(y)$ と変形することができます。
これは、偏差の期待値が 0 であることを示しています。
証明式です。
$V[a X+b]=$
$=\sum_{x}((a x+b)-E[a X+b])^{2} p(x)$
ここで、$E[a X+b]=a E[X]^{2}+b$ を代入すると、
$V[a X+b]=$
$=\sum_{x}((a x+b)-a E[X]-b)^{2} p(x)=$
$=a^{2} \sum_{x}(x-E[X])^{2} p(x)$ と式変形を行うことができます。
まとめ|期待値と分散

いかがでしたでしょうか。
式が多くて少々ややこしく感じるかもしれませんが、公式を忘れてしまった時に見直すツールにしていただければと思います。
本記事では
- 期待値・分散とは
- 期待値・分散の定義
- 期待値・分散の性質
- 期待値・分散の公式一覧の把握
について学習しました。今回は以上で終わりとします。
