こんにちは。
産婦人科医で現在人工知能やビッグデータ関連の研究を行っているTommy(Twitter:@obgynaitommy)です。
本記事では記述統計に重点を置きつつ、記述統計学と推定統計学の違いについて学習していきます。
対象としては、統計検定2級の取得を目指している方、または資格取得に限らず統計の基本的な知識を学びたい方に向けた記事となります。

データのまとめ方は平均値の他にも色々あります。
また、平均値でまとめることのできないデータもあります。
本記事では、記述統計と推測統計学の違いについて学習し、その後に各論である記述統計学と推測統計学について学習していきましょう。
記事統計学と推測統計学の違いとは

記述統計学とは今あるそのデータの特徴を分かりやすく説明することです。例えば「収集したデータの傾向や性質を把握する様なもの」です。
例として挙げると、
- 偏差値
- テストの平均点
などがあります。
一方で推測統計学とは、今あるデータから明らかにしたい大元の集団の特徴を推測する統計のことです。例えば以下のものがあります。
- テレビの視聴率
- 選挙の投票調査
記述統計学と推測統計学のイメージは、例として、視聴率で考えると分かりやすくなります。
例えば関東地区には約2,000万世帯ありますが、視聴率はランダムに選ばれた2,700世帯が見たテレビ番組を元に計算されます。
この2,700世帯のうち何%が視聴したかをまとめるのが記述統計学です。
一方推測統計学では、2,700世帯のデータから、その背後にある関東地区約2,000万世帯のデータを推測します。
推測統計ではいわゆる難しい数式を使って、一部のデータの特徴から全体のデータの特徴を見ようとします。
記述統計学の場合、無作為とはいえ適当に取ってきたデータだったら、何らかの特徴が見つかったとしても、たまたま取ってきた集団がそうだっただけという可能性があります。
しかし推測統計学の場合は全体のデータの特徴として推測するため、何らかの特徴が見いだされたら、それは全てのデータに共通するものとなります。
この全てのデータに共通するものが、いわゆる法則です。
"推測統計学を行うことで、法則を見出すことができる"のです。
それではまず、記述統計と推測統計の中でも、推定統計について簡単に学習していきましょう。
推測統計学とは

推測統計学とは、今あるデータから明らかにしたい大元の集団の特徴を推測する統計のことです。
推測統計学には、統計的推定と仮説検定の2つがあります。
統計的推定とは、今あるデータから明らかにしたい大元の集団の特徴を推測することそのものです。
例えば、国民健康・栄養調査15によると、2017年の日本人の成人男性の平均身長は167.6cmでした。
2017年時点の日本には約1.3億人います。
つまり、日本人男性は0.65億人ほどいます。
そのうち未成年は1/5としたとしても、0.52億人ほどはいることになります。
この平均身長は0.52億人の身長を測って出したものかというと、当然そんなことはありません。
この調査では日本の成人男性2,340人のデータの平均値をもって、日本の成人男性は167.6cmであると言っているのです。
このようなピンポイントで母集団の値を推定するのを点推定と言います。
とはいえ、集めたデータはあくまでも全体の一部であり、本当に正しいかと言われると誤差があると思います。
そのため、幅を持たせて日本の成人男性の平均身長は160cm ~ 170cmの間に含まれるということもあります。
このような幅を持たせた推定は区間推定と言います。
仮説検定とは、得られた標本のデータから母集団についてのある仮説が統計的に認められるものであるかどうかを確認することです。
例えば、アメリカの成人男性のほうが日本の成人男性よりも身長が高いイメージがあると思います。
ランダムにアメリカと日本の成人男性の身長データを集め、身長の平均値や身長データのばらつき、集めた人数を考慮して統計値を出していきます。
この統計値が確率論的に珍しい確率(95%以下)で出てくるものか調べることで、アメリカと日本の成人男性の平均身長の差は統計的に意味があるものか計算するのです。
なお、仮説検定はシンプルに2つのグループに差があるかだけではなく、3つ以上のグループに差があるかといったものや、数値データ同士の関連を調べるなど、様々なものがあります。
次に記述統計について学習していきましょう。
記述統計のうちデータの特徴を表現する様々な値について学びましょう。
記述統計とは【記述統計におけるデータの種類について】

データとは情報の表現であって、伝達、解釈または処理に適するように形式化され、再度情報として解釈できるもの。
"A reinterpretable representation of information in a formalized manner suitable for communication, interpretation, or processing."
例えば、データとは実験参加者(あるいはラットなどの被験体)を実験・調査することで得られた情報です。
量的変数・質的変数の違い【数値以外のデータについて】
データと言えば、血圧や心拍数などのように「数値」をイメージされているかもしれません。
しかし、データには数値以外のものもあります。
例えば、がん患者のデータを取る場合はがんのステージ分類「ステージⅠ」「ステージⅡ」「ステージⅢ」「ステージⅣ」のように、「順序」を意味するが「数値」ではないものもあります。
さらに血液型のように、順序もなく、単に他とは区別するだけのものもあります。
データの種類をまとめると、以下のようになります。
| データの種類 | |||
| 質的変数 ※ 離散変数と呼ばれることもある | 名義尺度 | 他と分類する基準 →他と区別しているだけであり、どちらが大きいなどの優劣はない。 | 性別(男性、女性) 血液型(A型、B型、O型、AB型) |
| 順序尺度 | 順序によって表されたデータ →大小は表現できるが、どのくらい差があるのかは分からない。 | がんのステージ分類(ステージ0, 1, Ⅱ, Ⅲ, Ⅳ) 徒競走の順位(1位, 2位, 3位) | |
| 量的変数 ※ 連続変数と呼ばれることもある | 感覚尺度 | 等間隔の数値目盛によって表されたデータ →「3℃」高いなど、数値としての比較が出来る。 | 温度(℃)、知能指数(IQ)など |
| 比例尺度 | 「0」からスタートする等間隔の数値目標 によって表されたデータ → 「2倍高い」の様に倍率を表す事ができる。 | 身長・血圧・体重・心拍など | |
ここで質的変数と離散変数には2種類あります。
質的変数あるいは離散変数
- 名義尺度
- 順序尺度
この2つの名称を抑えておきましょう。
量的変数または連続変数には2種類のものがあります。
量的変数あるいは連続変数
- 間隔尺度
- 比例尺度
ここで、名義尺度、順序尺度、間隔尺度、比例尺度のうち、名義尺度と順序尺度は質的変数あるいは離散変数とまとめられる事があります。
間隔尺度と比例尺度は量的変数あるいは連続変数とまとめられることもあります。
質的変数は分類する名前や順序など、足し算できない「性質」のデータです。
がんのステージ分類や徒競走の順位のように飛び飛びの値を取るので、数が離れている離散変数と呼ばれることもあります。
一方、量的変数は数値なので、足し算できる「数量」のデータです。
温度や身長のように数値がずっと続いているデータなので、連続変数と呼ばれることもあります。
なぜデータの種類のお話から始めるかというと、実はデータの種類によってデータのまとめ方が変わってくるためです。
平均・中央値・最頻値・外れ値について
「データをまとめると言えば平均値」は誤りです。
集めたデータの特徴を簡単に表現する値のことを代表値と言います。
代表値には平均値や中央値、最頻値など、色々あります。
平均値
代表値のなかで皆さんによく知られているのは平均値だと思います。
平均値とは、全てのデータの値を足したものをデータの数で割ったものです。
以下の式で表されます。
$$平均值 =\frac{\text { データ1 の值 }+ { データ2 の值 }+{ データ3 の值 }+\cdots { データ n の值 }}{\text { データ の個数 }}$$
これを数式にすると、以下のようになります。
・\(\overline{\mathbf{x}}\):平均値
・\(x_{1}\):1番目のデータ
・\(\mathbf{n}\):データの数
平均値で表せられるものは身長や体重、血圧などの量的変数です。
実は、これらのデータにはもうひとつ共通点があります。
それは、全てのデータを並べると以下の図のように左右対称の山型になるということです。
例えば、以下の図は6歳女児の平均身長の分布です。
115cmが頂点となり、左右対称の山の形になっています。
なお、この左右対称の山型の分布は正規分布と呼ばれます。
正規分布は推測統計のお話をするときにも出てきますので、覚えておきましょう。
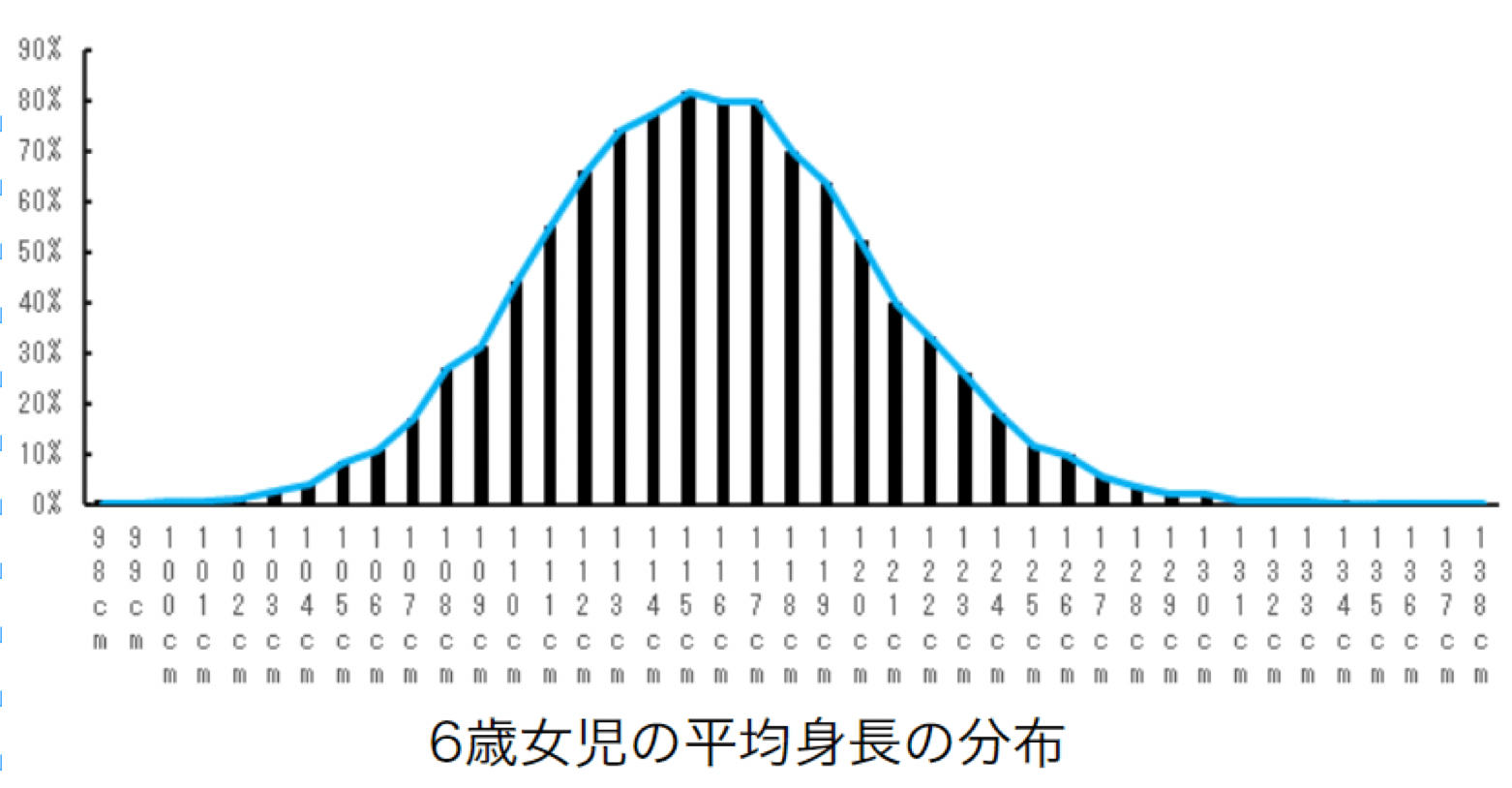
6歳女児の平均身長の分布 【出典】令和元年度学校保健統計調査より
中央値
全てのデータを並べたときに左右対称にならないデータとして、世帯ごとの所得があります。
日本の世帯ごとの平均所得は551万6千円です。
世帯には共働世帯だけではなく独身世帯や単親世帯、引退した高齢者世帯も含まれるのに、551万円6千円は高い気がしませんか?
なぜ、平均所得が高いかというと、所得が1億円以上といった非常に高所得な世帯もあるためです。
全てのデータを足して求める平均値は非常に大きな値に左右されてしまいます。
こういった平均値の欠点が補われているのが、中央値です。
中央値とは、全てのデータの値を小さいものから大きいものまで順番に並べたときにその真ん中に来る値のことです。
※データの数が偶数の場合、真ん中の値2つを足して2で割ったものが中央値になります。
日本の世帯ごとの所得の中央値は423万円です。
何となく、実感が湧く数値になった気がします。
中央値は以下の図のように、左側あるいは右側に偏った山型の分布のときに使われます。
なお、中央値と平均値をグラフ上にプロットすると、図の通りになります。
やはり平均値は大きな値に引っ張られていることが分かりますね。
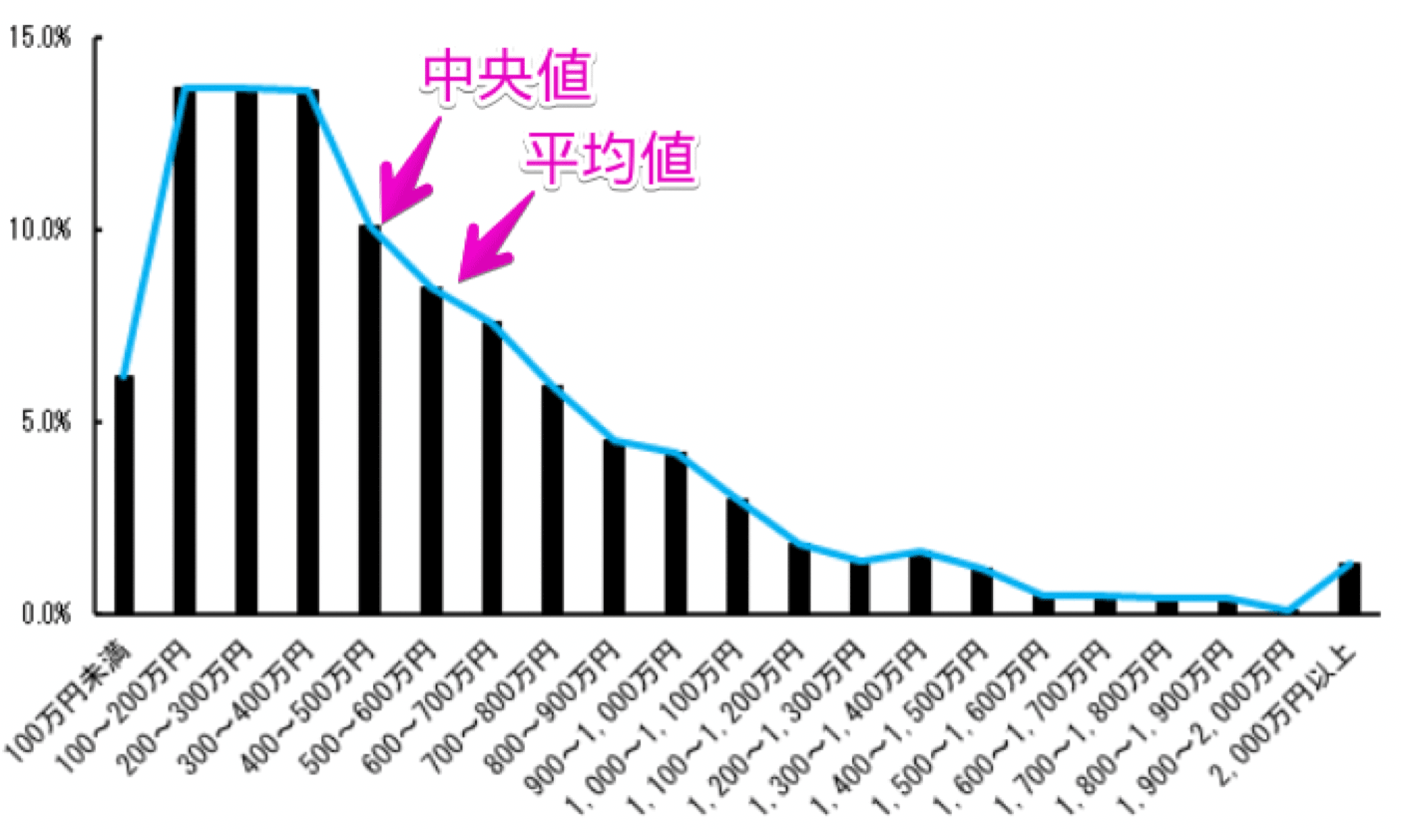
所得ごとの世帯の割合 【出典】平成30年度 国民生活基礎調査
最頻値
質的変数の代表値の出し方はどうなるかというと、非常にシンプルです。
一番出てきた数が多いものが代表値となります。
この代表値は「最も頻度の高い値」と書いて、最頻値(モード)と呼ばれます。
例えば、以下の架空のがん患者のデータを見てみましょう。
| 番号 | がんのステージ |
| 1 | Ⅰ |
| 2 | Ⅰ |
| 3 | Ⅰ |
| 4 | Ⅱ |
| 5 | Ⅱ |
| 6 | Ⅱ |
| 7 | Ⅱ |
| 8 | Ⅲ |
| 9 | Ⅲ |
| 10 | Ⅲ |
ステージⅠが3人、ステージⅡが4人、ステージⅢが3人います。
よって、一番人数の多いステージⅡが最頻値となります。
ちなみに、最頻値は質的変数だけではなく量的変数でも出すことはできます。
一番出てきた数が最も多いのが最頻値なので、正規分布でいうと山頂が最頻値となります。
日本の世帯ごとの平均所得の分布の最頻値は以下のようになります。
-min.png)
所得ごとの世帯の割合 【出典】平成30年度 国民生活基礎調査
ただ、最頻値はざっくりとした表現であり、データ数が多いものでなければ、あまり意味がなくなります。
先ほどのがん患者のデータでも、4人のステージⅡが最頻値ではありましたが、3人のステージⅠもステージⅢもあまり人数に違いがありませんでしたよね。
このように、最頻値では最もその項目が多いこと以外、情報があまりありません。
そのため、量的変数の代表値では平均値あるいは中央値のほうがよく使われます。
外れ値
平均値を出すときには全てのデータを使うべきだと思っていませんか?
データを扱うときには誠実でなければならないのは、データ分析を行う上での基本的姿勢です。
しかし、以下の架空の高血圧者の最高血圧のデータを見てください。
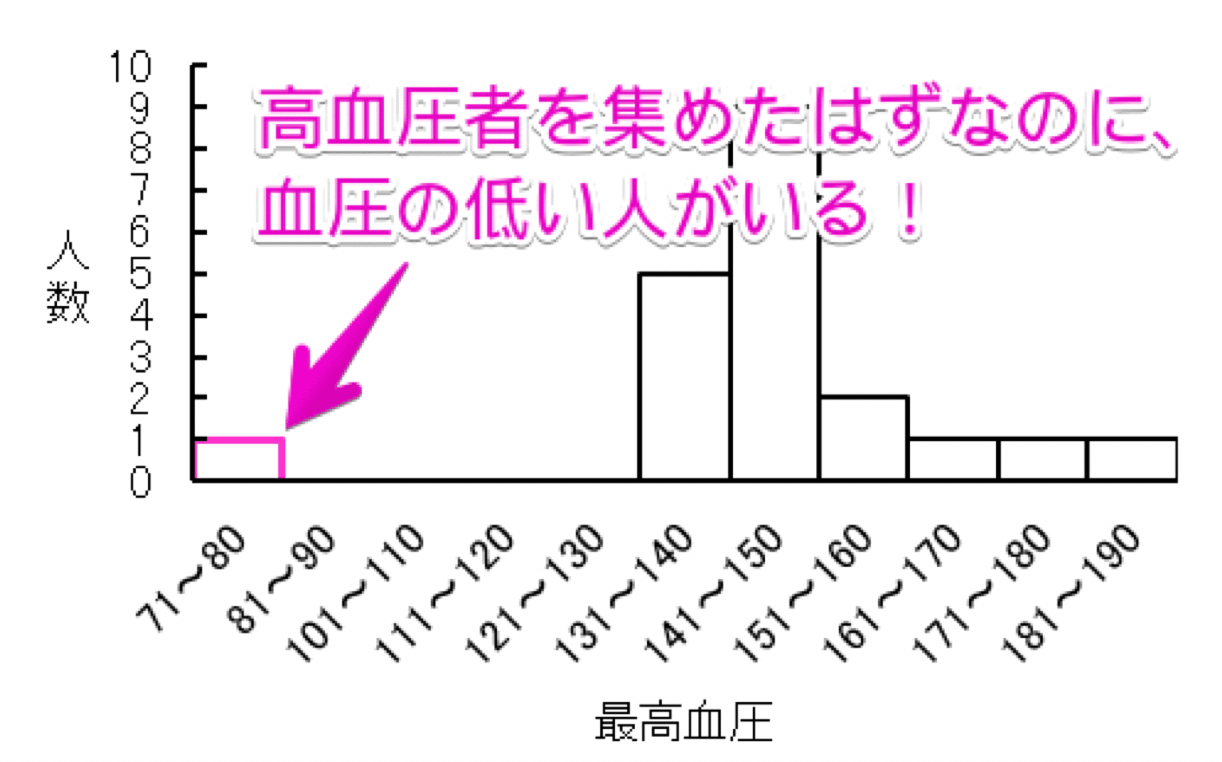
高血圧者の最高血圧のデータ【架空のデータ】
高血圧者の最高血圧のデータを集めたはずなのに、最高血圧が71~80mmHgだった人がいます。
このように、他の値から大きくずれた値のことを外れ値と言います。
外れ値があると、正しい結果が出せません。
そのため、外れ値は除いたほうが良いです。
なお、今回のデータは「高血圧者の最高血圧」だったため、外れ値とみなしてデータを除きました。
これがもし一般成人の高血圧のデータだったなら、外れ値とはなりません。
※もっとも、何の意図もなく一般成人から集めたデータのほとんどが高血圧者なので、それはそれとして、データの集め方の問題はありますが。
外れ値とみなすかどうかは、目的と照らし合わせて行いましょう。
安易にデータを消し去るのは、誠実な姿勢で統計分析を行うべきという姿勢に反しています。
分散・標準偏差・変動係数について
中学2年生でハンドボール投げ25mのA君と小学5年でハンドボール投げ25mのB君。
B君のほうが統計的に見てもすごいことを、お話しします。
同じ距離なら、年齢の低い小学5年生B君のほうが中学2年生A君よりすごいと何となく思うでしょう。
でも、平均値とデータのばらつき(これを標準偏差と呼びます)を考えたら、客観的にB君のほうがA君よりすごいと言えるのです。
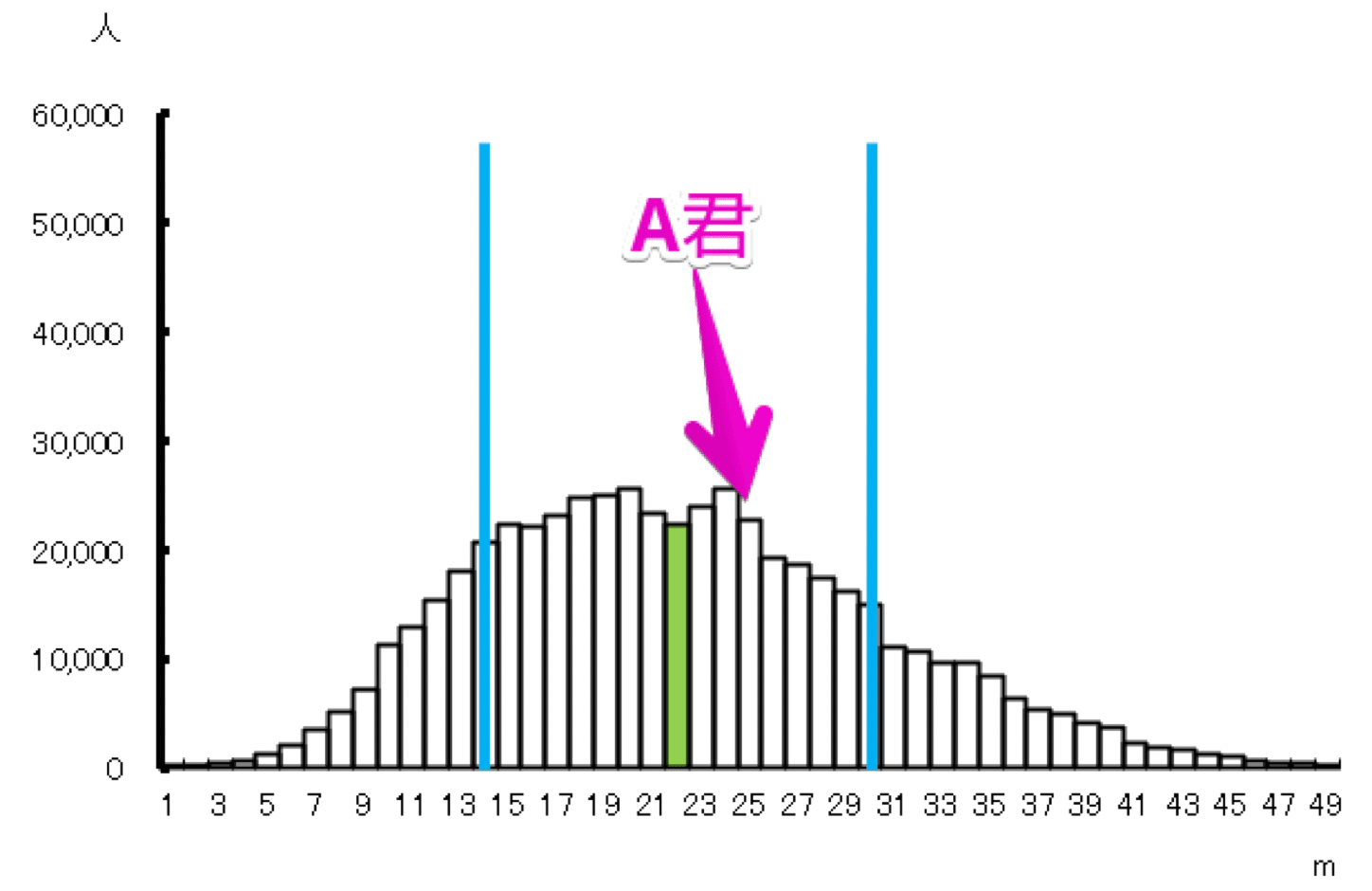
中学2年生と小学5年生のハンドボール投げの分布のグラフを見ていきましょう。
黄緑の棒が平均部分で、青色は標準偏差の範囲です。
青色の棒と棒の間には約70%(正確には68.2%)の人がいます。
まず、A君を含む中学2年生のハンドボール投げの分布は以下の通りです。
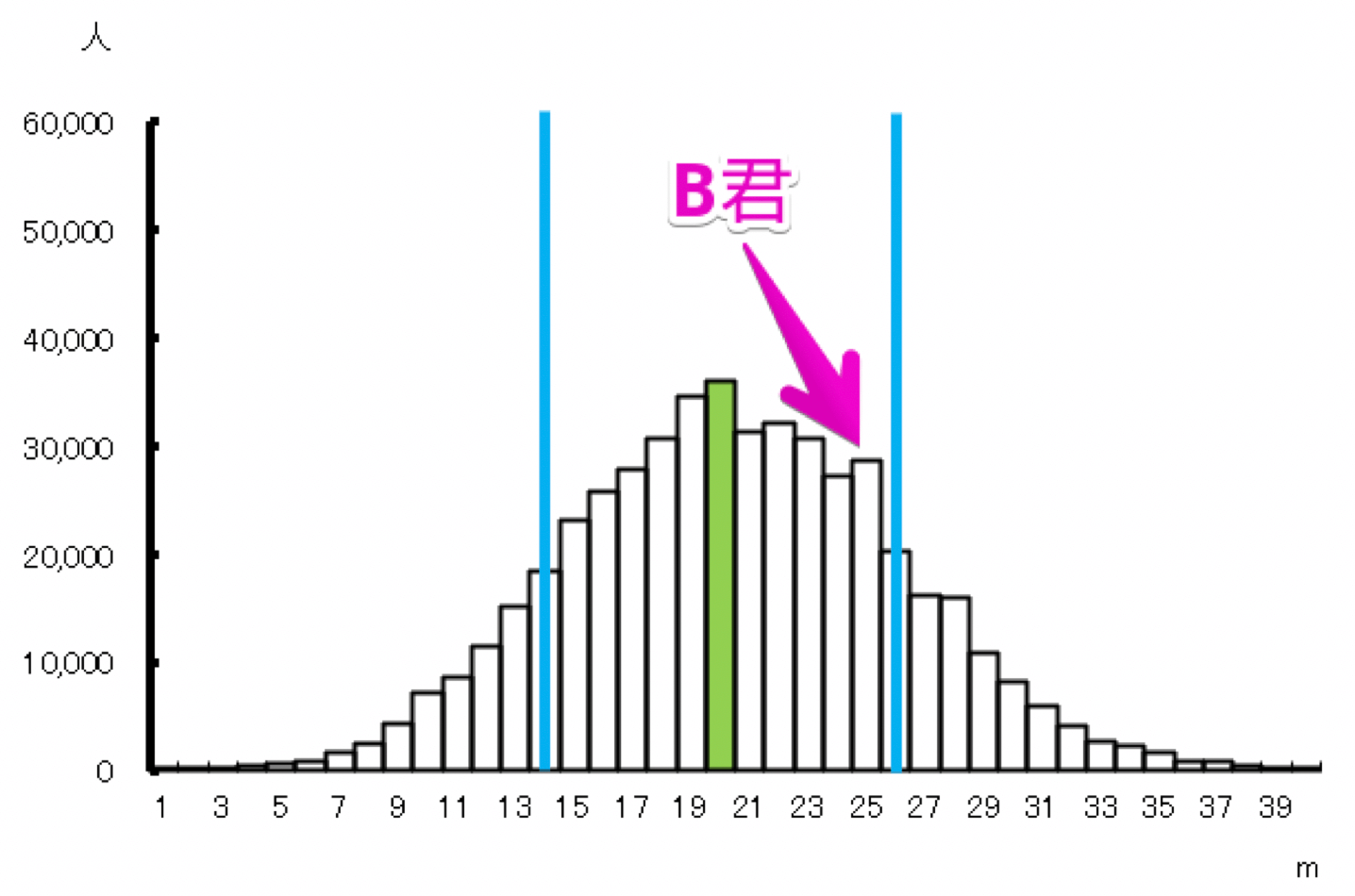
次に、B君を含む小学5年生のハンドボール投げの分布は以下の通りです。
A君は分布の中で平均値に近いですが、B君は平均値に標準偏差を加えた値の近くにいることが見て取れます。
ざっくりした計算になりますが、分布のなかでのA君の位置づけは大体真ん中あたりなのに対して、B君は真ん中というより上位30%~40%ぐらいの位置にいます。
このことから、A君はボール投げが平均的なのに対し、B君は平均よりも優れていると言えるため、B君のほうがA君よりもすごいと言えるのです。
標準偏差
バラツキを表現する標準偏差ですが、平均値と同じように公式があります。
以下の式で表されます。
これを数式にすると、以下のようになります。
\(S=\sqrt{\frac{1}{n} \sum_{n=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\)
・\(S\):標準偏差
・\(x_{i}\):i番目のデータ
・\(n\):データの数
・\(\overline{\mathbf{x}}\):平均値
イメージは、一つひとつのデータと平均値のズレを出していき、それを2乗してから、1個あたりの平均とのズレを求めるという感じです。
なぜ2乗するかというと、平均値よりもプラスでズレている値もあれば、マイナスにズレている値もあるためです。
最後にルートを取ることで、2乗してズレていた単位を元の平均値と同じ単位の土俵に乗せることができます。
先ほど、ハンドボール投げのグラフで大体の標準偏差の位置を水色のバーで示していましたが、それができるのも平均値と標準偏差が同じ単位だからです。
分散
標準偏差と同様に、分散もバラツキを意味します。
分散は以下の式から求めます。
これを数式にすると、以下のようになります。
$$S^{2}=\frac{1}{n} \sum_{n=1}^{n}\left(\mathrm{x}_{i}-\overline{\mathrm{x}}\right)^{2}$$
・$S^{2}$:分散
・$\mathbf{x}_{i}$:i番目のデータ
・$n$:データの数
・$\overline{\mathbf{x}}$:平均値
多くの方が気づかれている通り、標準偏差を2乗したものが分散です。
平均値同じ単位の土俵で話せるということで、標準偏差のほうが記述統計ではよく用いられます。
分散が一番必要とされるのは、分散分析のところです。
分散分析では、偶然によるデータの散らばり(分散)と条件の違いによるデータの散らばり(分散)の比較を行って、条件の違いのほうが偶然よりも勝っているかを分析します。
詳しいお話は、講座④で行います。
今は、分散は標準偏差を2乗したものだと覚えてもらえれば大丈夫です。
変動係数

データの分布の頂点が右や左に極端によっている場合は、変動係数というものを使います。
変動係数は以下の式から求まります。
$$変動係数 =\frac{\text { 標準偏差 }}{\text { 平均值 }}$$
これを数式にすると、以下のようになります。
$$\mathrm{CV}=\frac{s}{\overline{\mathrm{x}}}$$
・\(\mathrm{CV}\):変動係数
・\(S\):標準偏差
・\(\overline{\mathbf{x}}\):平均値
変動係数も分散と同じで単位はありません。
なお、変動係数にはひとつ注意点があります。
それは、平均値を標準偏差で割るというように、倍率で表すことができるデータ「比例尺度」にしか使えない点です。
同じ量的変数であっても、比率尺度には使えない点には注意が必要です。
標準化(z得点)について

数学と国語の得点からは、一概にどちらのほうが得意と比べることはできません。
でも、数学と国語の「偏差値」を見て、どちらのほうが得意と言うことはできましたよね。
その理屈は以下の通りです。
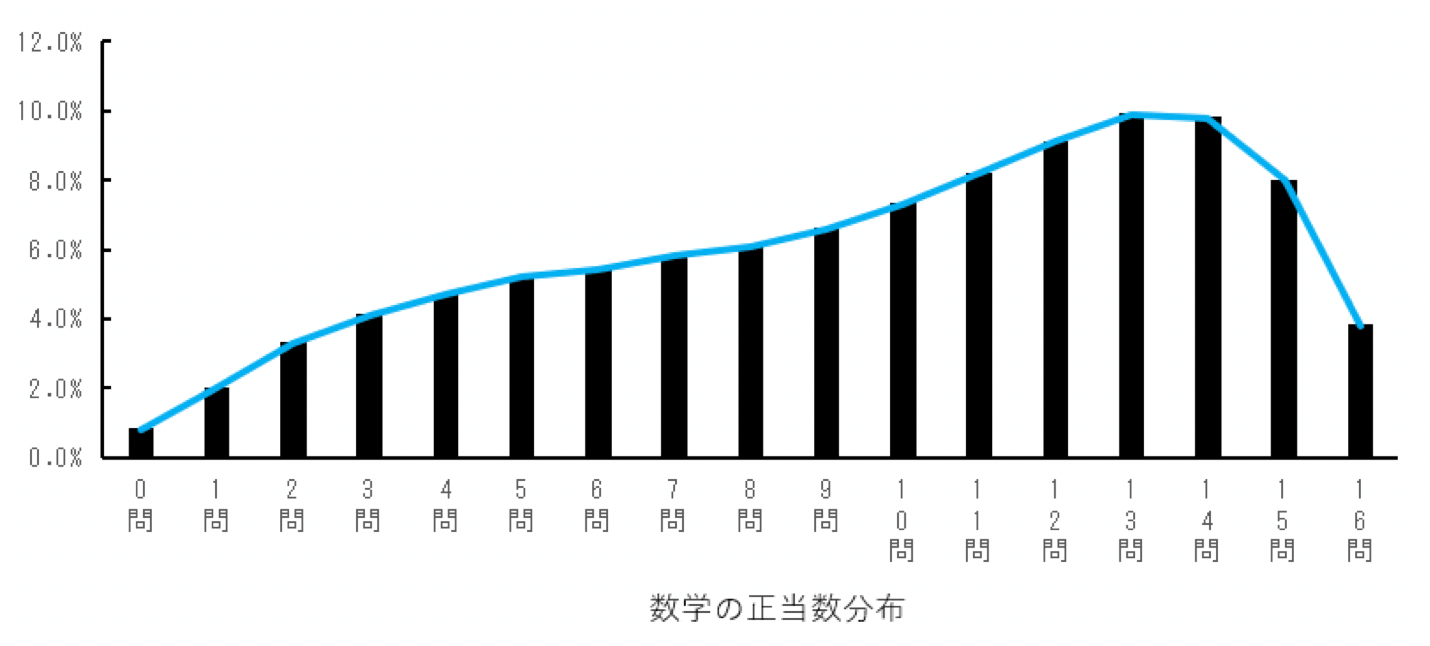
国立教育政策研究所が報告した平成31年度(令和元年度) 全国学力・学習状況調査 調査結果資料によると、中学3年生の数学の正当数分布は以下の通りでした。
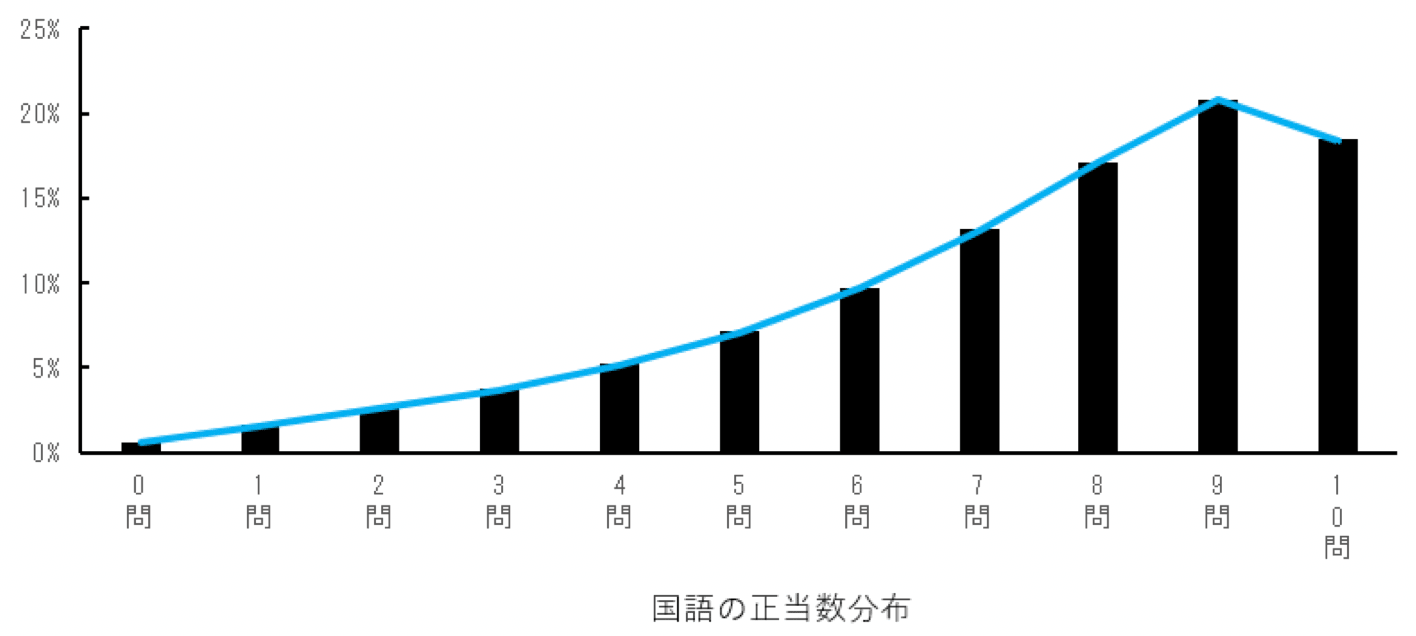
一方、国語の正当数分布は以下のようになりました。
それぞれ、正当数の分布は右側に頂点が寄っている点は似ていますが、問題数も平均正当数も違って、そのままでは比較できません。
この分布の平均を0に、標準偏差を1にした正規分布にするのが標準化です。
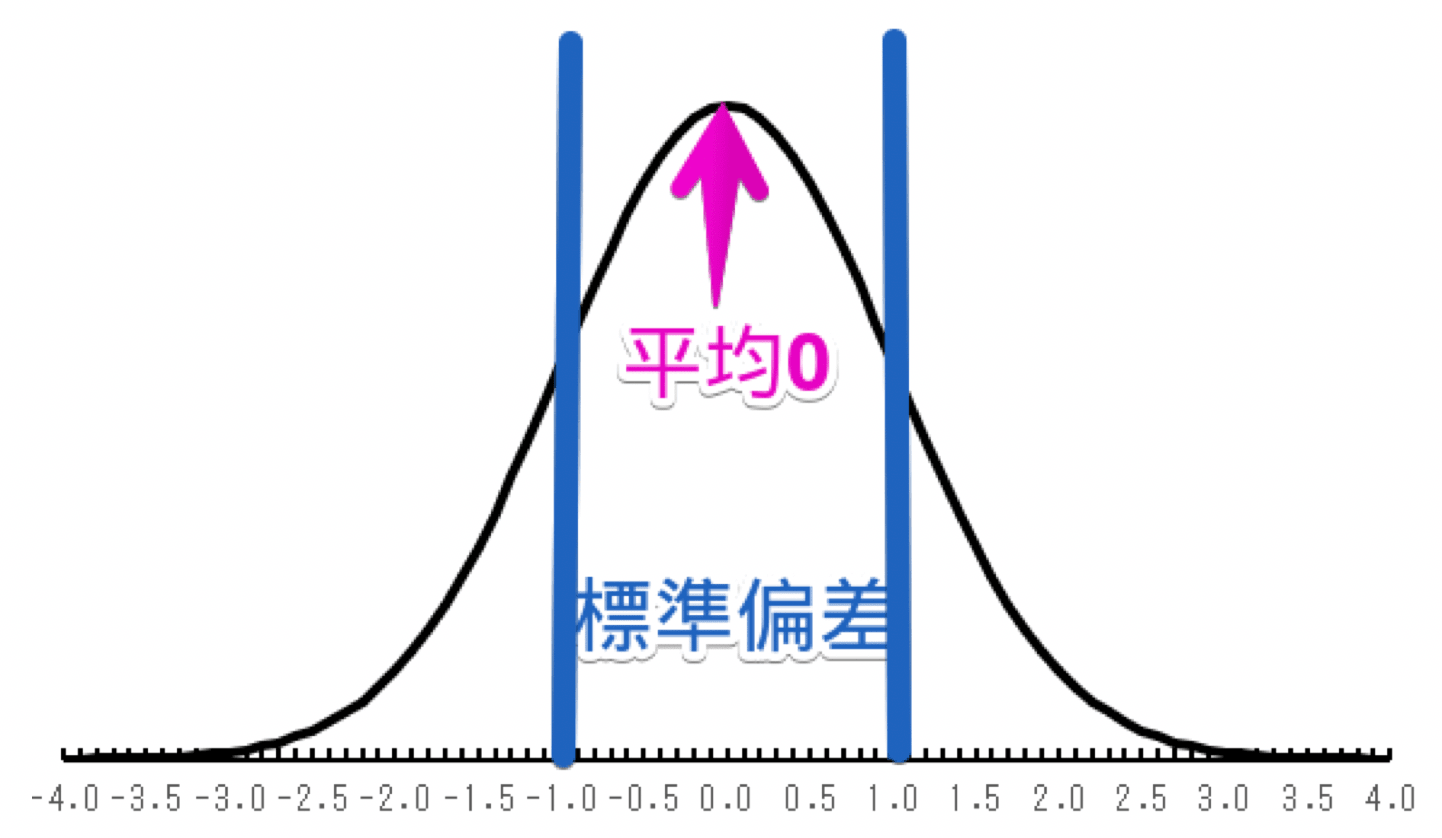
標準化:分布の平均を0に、標準偏差を1にした正規分布
標準化することで同じ形の分布で比較できるので、標準化した得点(標準得点と言います)は比べることができるのです。
得点を標準化するには、以下の式のように平均値と標準偏差が必要です。
$$標準得点 =\frac{\text { ある得点 }-\overline{\mathrm{x}}}{\mathrm{s}}$$
これを数式にしたのが以下の式です。
$$標準得点 =\frac{x-\bar{x}}{S}$$
・$X$:ある得点
・\(\overline{\mathbf{x}}\):平均値
・\(\mathrm{S}\):標準偏差
実際に標準得点を出してみましょう。
数学のテストでは10問、国語のテストでは7問正答した学生がいたとしましょう。
平成31年度(令和元年度) 全国学力・学習状況調査 調査結果資料によると、数学のテストの平均値は9.7問、標準偏差は4.2問で、国語のテストの平均値は7.3問、標準偏差は2.4問でした。
先ほどの式に入れると、数学の標準化した得点は $\frac{10-9.7}{4.2}=0.007$となりました。
一方、国語の標準化した得点は$\frac{7-7.3}{2.4}=-0.125$となりました。
こうして、この学生は数学のほうが国語よりも得意だと分かりました。
なお、偏差値も実は標準化された得点の一種で、平均が50、標準偏差が10になるように調整されているものです。
練習問題

平均値・中央値の確認
問題①:階級値について
次の表は,架空の血圧データです。
| 階級 | 度数 |
| 80〜90mmHg | 5 |
| 100〜119 mmHg | 15 |
| 120〜139mmHg | 10 |
| 140〜159mmHg | 5 |
この度数分布表から血圧のおおよその平均値を求めてください。
→度数分布表から平均値を求めるには、「階級値」を使います。
階級値とは、それぞれの階級の平均値です。
階級値を求めた結果、以下のようになりました。
| 階級 | 階級値 | 度数 |
| 80〜99mmHg | 89.5 | 5 |
| 100〜119mHg | 109.5 | 15 |
| 120〜139mmHg | 129.5 | 10 |
| 140〜159mmHg | 149.5 | 5 |
あとは、平均値の公式を使って以下のように求めます。
問題②:中央値について
次の表は,平成30年度全国体力・運動能力、運動習慣等調査で小学校5年生の女子の握力についての相対度数分布表です。
| kg | 相対度数 |
| 5 | 0.06% |
| 6 | 0.14% |
| 7 | 0.30% |
| 8 | 0.63% |
| 9 | 1.28% |
| 10 | 2.60% |
| 11 | 4.44% |
| 12 | 6.59% |
| 13 | 8.66% |
| 14 | 10.48% |
| 15 | 11.29% |
| 16 | 10.81% |
| 17 | 9.80% |
| 18 | 8.27% |
| 19 | 6.70% |
| 20 | 5.37% |
| 21 | 3.93% |
| 22 | 2.82% |
| 23 | 1.98% |
| 24 | 1.38% |
| 25 | 0.93% |
| 26 | 0.60% |
| 27 | 0.37% |
| 28 | 0.23% |
| 29 | 0.15% |
| 30 | 0.09% |
| 31 | 0.05% |
| 32 | 0.03% |
| 33 | 0.02% |
| 34 | 0.01% |
握力が中央値よりも低い人は何%いますか?
尚、2019年11月の統計検定2級ではこれと似たような問題が出題されました。
問題③:最頻値について
次の表は、架空の血圧のデータです。
| 1 | 100mmHg |
| 2 | 101mmHg |
| 3 | 102mmHg |
| 4 | 104mmHg |
| 5 | 104mmHg |
| 6 | 104mmHg |
| 7 | 108mmHg |
| 8 | 114mmHg |
| 9 | 115mmHg |
| 10 | 118mmHg |
| 11 | 121mmHg |
| 12 | 125mmHg |
| 13 | 125mmHg |
| 14 | 125mmHg |
| 15 | 128mmHg |
| 16 | 141mmHg |
| 17 | 143mmHg |
| 18 | 145mmHg |
| 19 | 150mmHg |
| 20 | 159mmHg |
最頻値は何ですか?
→104mmHgと125mmHg
最も出てくる頻度が高い値が最頻値なので、平均値や中央値と違って、最頻値が複数のこともあります。
問題③:標準偏差・分散・変動係数について
以下は、架空の算数のテストの得点です。標準偏差・分散・変動係数を求めてください。
| 1 | 50点 |
| 2 | 60点 |
| 3 | 78点 |
| 4 | 44点 |
| 5 | 82点 |
| 6 | 33点 |
| 7 | 56点 |
| 8 | 89点 |
| 9 | 45点 |
| 10 | 61点 |
→まず、このデータの平均値は60.3です。
よって、これを標準偏差の公式を使うと、標準偏差を求めることができます。
$\sqrt\frac{(50-60.3)^{2}+(65-60.3)^{2}+\ldots(61-60.3)^{2}}{10}=17.32$
分散は標準偏差を2乗したものなので、標準偏差を求める途中で出た300.01がそうです。
変動係数は、標準偏差を平均値で割ったものなので、0.29です。