機械学習のうち教師なし学習を行う際に必要なクラスタリングには、主に以下の種類があります。
- 階層型クラスタリング(Agglomerative Nesting(AGNES))
- 非階層型クラスタリング(K-measns法)
- スペクトラルクラスタリング
- 自己組織化マップ(SOM)
中でも特に良く使用される手法は上の2つにある階層型クラスタリング、非階層型クラスタリングです。
今回はこれらの2つを中心に解説していきます。
階層型クラスタリング

階層型クラスタリングについて解説していきます。階層型クラスタリングにはボトムアップ型とトップダウン型の2種類があります。
この記事ではボトムアップ型の解説をしていきます。
「ボトムアップ型の階層型クラスタリング」とはすなわち、それぞれの点同士の「距離」を比べて、近い点同士を繋げてボトムアップでまとめていくアルゴリズムです。
その際に「距離」をどの様に定義するのかがポイントです。距離とは基本的に「ユークリッド距離」すなわち「ものさしで長さを測る距離」を指します。
ポイント
階層型クラスタリングのように毎回すこしずつクラスタを変化=成長させていく方法はボトムアップ型あるいは凝集型(agglomerative)方法と呼ばれます。
また逆に、ひとつのクラスタを分割する方法はトップダウン的あるいは分割型(divisive)の方法と呼ばれます。
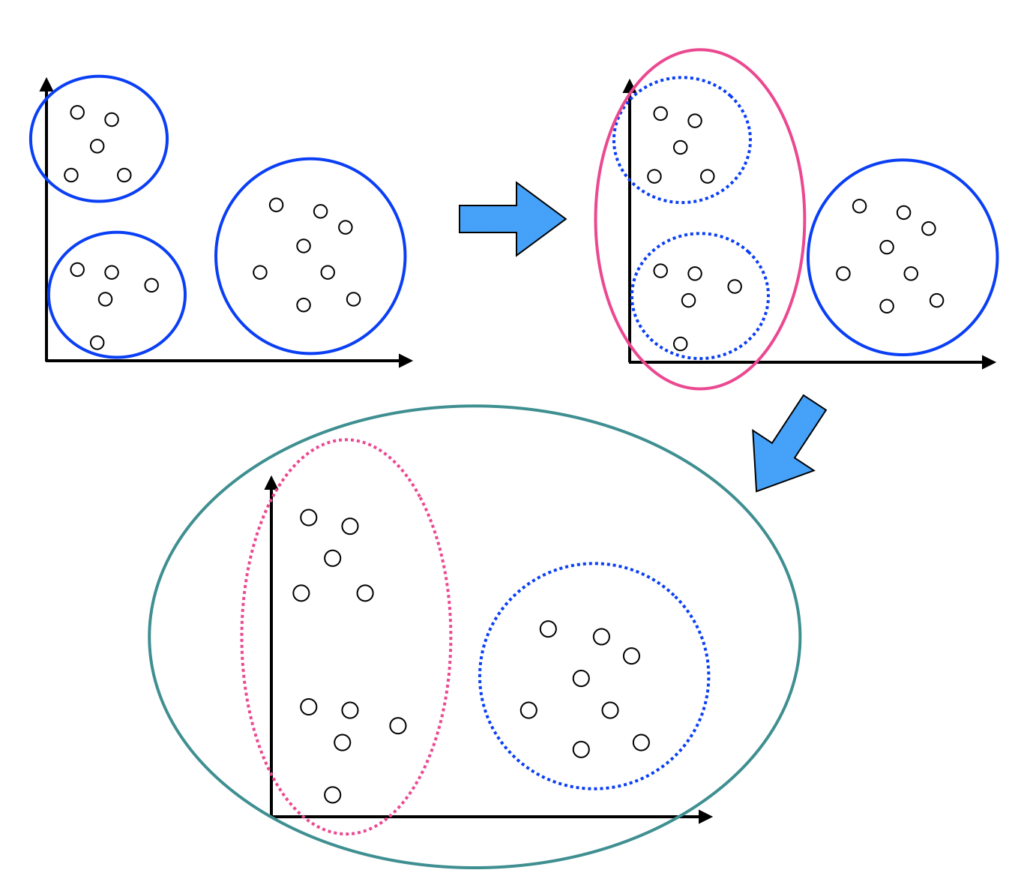
「階層型クラスタリング」のイメージは以下の様な図で表すことができます。
まず、近いもの同士をグループにして、作成したグループ同士を合併させて、更に大きなグループを作ります。
これを繰り返していくわけです。最終的には全てのグループで全ての点が一つのグループになります。どこでグループ同士の結合をやめるのかがポイントとなります。
階層型クラスタリングのアルゴリズム
a, b, c, d, e, f, g, h, i, j の10個のデータがあるとします。
aとaの距離は0で、aとbの距離は2、aとcの距離は4というように以下の様な距離が定められているとします。
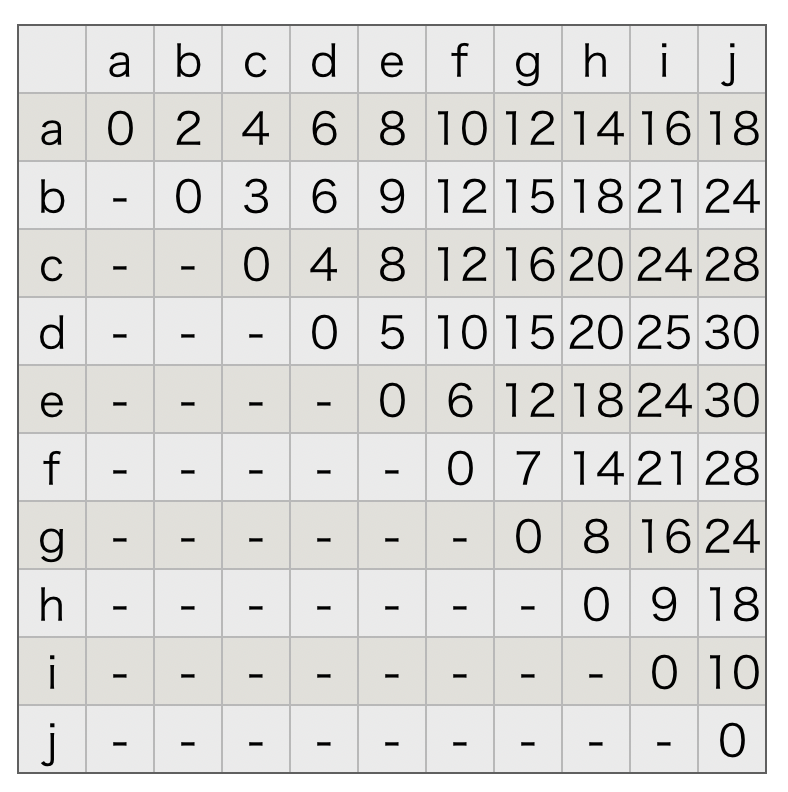
階層型クラスタリングのアルゴリズム 【距離行列の例】
階層型クラスタリングではこの様に、距離の行列を使用してボトムアップでデータをまとめます。
ボトムアップでのデータをグループ分けする過程を以下の様な略式図で表すことができます。
このグラフのことを「デンドログラム」と言います。
デンドログラムの見方ですが、まずは左図のa点とb点に注目すると、a点とb点が結合していることが分かります。この2つの距離が近かったため、初期段階で結合されたことが分かります。
デンドログラムの中央付近を見るとe点、f点が結合しています。次にe点f点が結合したグループとg点が結合し、h点と更に結合します。
距離の近いデータ同士を次々に結合させてい区ことで、最終的には全てのデータの点が一つの集塊=クラスターになります。
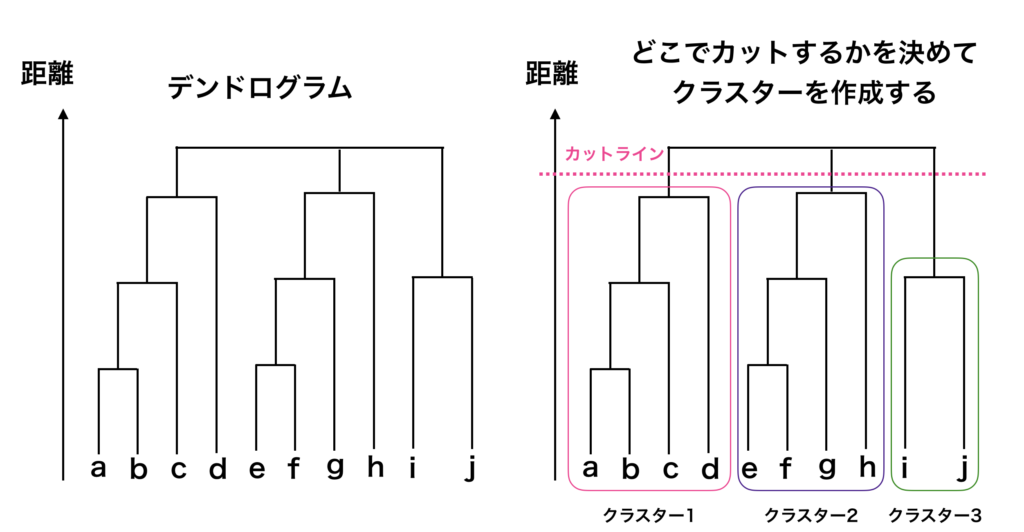
ここで、最終的にどの様にクラスターを作成するかですが、階層型クラスタリングでは、デンドログラムを確認して、どの辺でデンドログラムを切るのか、でクラスタリングが決定します。
右図では点線のラインでデンドログラムをカットしているため、クラスターが5つになっています。
この様にクラスターを分けることで、それぞれのクラスターにどのデータの点が含まれているのかが分かります。
階層型クラスタリングのメリットとしては、視覚化して分かりやすいことです。
デンドログラムを見るたけで、どの点と点が近いのかがすぐに分かりますし、クラスターの略式図も理解する事ができます。
一方で、階層型クラスタリングのデメリットとしては、データの数が多いとデンドログラムが見えにくいという事があります。
大量のデータを処理して、デンドログラムを確認したい際にはサンプリングなどを行う事で、データの点を減らす必要があります。
非階層型クラスタリング【K-means法】について
非階層型クラスタリングの手法である K-means法について解説します。
K-means法とは、予め分析する者がデータをいくつかのクラスターに分けておくか事前に決めておいてからデータを分割する方法です。
非階層型クラスタリングのポイントは、分析者が事前にクラスター数を決めておく、という点です。
また、一方で階層型クラスタリングの場合にはクラスターの数は事前にわかておくことはしません。
というのも階層型クラスタリングはボトムアップで最後は全てを一つのクラスターにまとめるためです。
階層型クラスタリングはクラスタリングをする上で何の前提も必要としない一方で、どこまでを「求めたいクラスター」とするのかを決めるのが難しい場合があります。
これから解説するK-means法では、クラスターの数は事前に分析者が決めておく必要があります。
K-means法のアルゴリズム
K-means法のアルゴリズムは以下のステップで行います。
K-means法のアルゴリズム
- あらかじめ自分でクラスター数を決めておく。(例えばクラスター数を $K$ とする)
- データに対して、乱数を使用してランダムに $K$ 個のデータ点を選ぶ。選ばれたサンプルを「シード」という。
- 各々のデータについて、最も近いシードを求めてそのシードにデータを割り当てていく。全てのデータは $K$ 個のシードのうちのいずれかに割り付けられる。割り当てたデータを使用して、クラスタの平均値(中心)を計算する。
- 計算されたクラスタの平均値(中心)を利用して、各データを最も近いクラスタに割り当て直す。
- 3–4のステップを、最終的にクラスターの重心が安定するまで繰り返す。
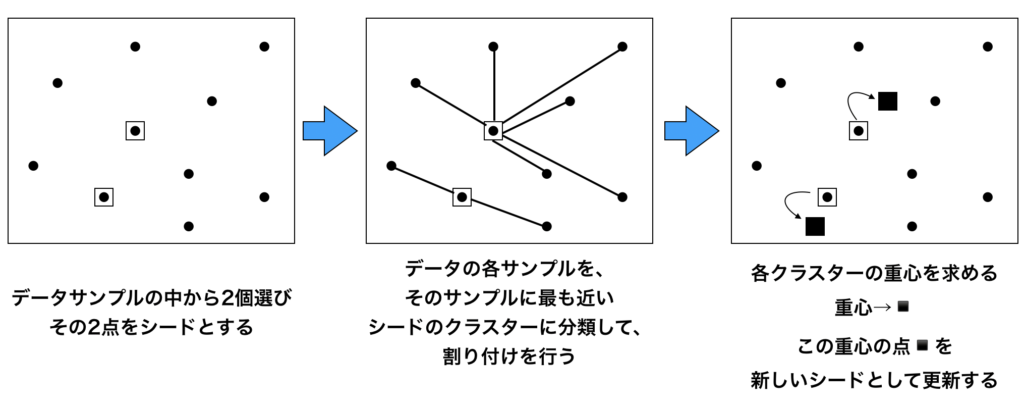
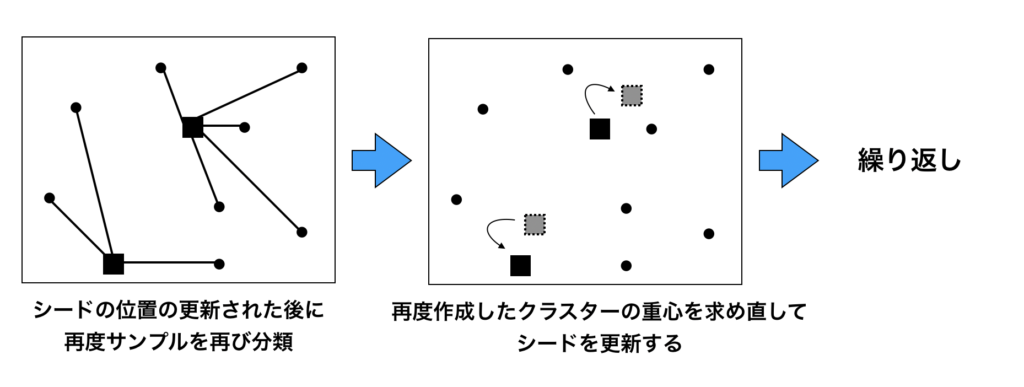
以下にK-means法のアルゴリズムを可視化したシェーマを図で紹介します。
上の図では、まずデータを2つのクラスターに分類しています($K=2$)
データのうち2つの点をランダムに選択し、この2点をシードとします。
全てのデータが2つのシードのうち、どちらに近いのかを距離を測定して計測します。
そして、各々のデータを近い方のシードに所属するクラスターに割り付けを行います。
クラスターに割り付けると、各々のクラスターの平均、すなわちクラスターの重心を求めます。この重心点を新しいシードとして、シードを更新していく作業をひたすら繰り返します。この手順を繰り返していくと、
いずれシードが動かなくなりますので、この状態が一番良い状態として分かれている、と考えるのがK-means法の考え方になります。
K-means法
$$\sum_{i=1}^{K} \sum_{x \in X_{i}}\left\|x-\mu_{i}\right\|^{2}$$
- \(\mu_{i}\) :各クラスターの重心
- \(X_{i}\) :各クラスターのデータ
- \(K\) :クラスター数
この数式が意味することは「各クラスターの重心とそのクラスターに割り付けられたデータとの距離の総和」のことはWithin-cluster sum of squares(WCSS)と言います。
しかし、「最初のシードとなるデータの点の選び方」を適当にばらまくのではなくて、さらに良い置き方があるのではないかということで考案されたのが K-means++(プラスプラス)法というアルゴリズムです。
K-means++法について
シードとなるデータの点を選ぶ際に、各々のシードとなるデータの点が離れるように点を選択するというのがコンセプトとなる。
K-means++ 法のアルゴリズム
- データ点の中からランダムに1つ選択してシードとする。
- 1つ前のシードと各データ点との距離を測る。
- 以下の確率で次のシードを選ぶ。(あるデータの点と一番近いシードまでの距離)^2/Σ(各データの点とその点が属するクラスターのシードまでの距離)^2
- シードが $K$ 個選ばれるまで上の2つを繰り返す。
- $K$ 個のシードが選択されたら、K-means法と同軸シードを更新する。
K-measn++ 法のアルゴリズムは、K-means法と同様に分析者が予めいくつのクラスターに分けたいのかを決めておく必要があります。
K-means++ 法の1つ目のシードの選び方は、K-means法と同様に、データの中からランダムに1点選びます。
続いて、2点目のシードを選ぶ必要があるのですが、ここがポイントとなります。
2つ目のシードも確率的に選択することになるのですが、選び方が通常のK-means法とは一味違います。
どの様に選択するのかというと、「1つ目のシードとそれぞれのデータの点との距離の2乗」を「1つ目のシードと、クラスターに属する各データの点の距離の2乗の合計」で割った値を確率として選びます。
要するにこれは1つ目のシードからクラスターに属する点の距離が遠ければ遠いほど、2番目のシードとして選ばれやすくなるわけです。(距離が遠くなればなるほど上の式からわかる様に確率が上がるためです。)
3番目のシードも確率的にシードを選択するのですが、使用する確率は「3番目に選択予定のシードと、1つのシードまたは2つ目のシードのうち、近い方からの距離の2乗」を「各点と1つ目のシードまたは2つ目のシードの近い方から距離の2乗の合計」で割った確率を基準に3番目のシードを選択します。
この様にすることで、1番目のシード及び2番目のシードからなるべく遠い距離をとって3番目のシードとして選ばれやすくなります。
これを分析者が決めたシードの数の分だけなんども繰り返して、$K$ 個全てのシードを配置します。
そのあとは K-means法と全く同じ様に、各データを最寄りのシードのクラスターに割り付けて、クラスターの平均値=クラスターの重心を繰り返し計算して、ある程度収束したところで、計算を終了します。
まとめですが、K-means++ 法はすでに置かれたシードからなるべく遠い位置に次のシードが配置されやすい様に、重み付けした確率を用いることがポイントです。
最適なクラスターの求め方

高次元になった場合の最適なクラスターの数の決め方については色々方法があります。
有名なところでいうと、以下の3つがあります。
クラスターの数の決め方
- Elbow method(エルボ・メソッド)
- シルエットプロット
- 階層型クラスタリングを使用した方法
より良いクラスタリングを行うためには2つのポイントがあります。それは「conhesion(凝集性)」と「separation(分離性)」の2つです。
良いクラスタリングというのは、クラスター内部のデータ自体が凝集されていて(cohension(凝集性))、クラスター同士の距離や間隔が離れている(separation(分離性))ということです。
クラスター内部のデータが凝集して、なおかつクラスター同士が離れている時(分離性)には良いクラスタリングと言うことができます。
最適なクラスター数を決める際には、この「conhesion(凝集性)」と「separation(分離性)」の2つに念頭を置きつつ決めるのが鉄則です。
Elbow method
Elbow method は各クラスター同士の conhesion(凝集性)に着目した方法です。
すなわち、各クラスター距離の総和(Within-cluster sum of squares: WCSS )を取りこのWCSSに着目した方法がElbow methodになります。
ここで、クラスター数を1から順番2, 3, 4と増やしていくと、各々の「クラスターの距離感が短くなる=WCSSが小さくなるのがわかります。
ここで、クラスター数を増やしていくと、急激にWCSSが現象するポイントがあり、この点の部分が最適なクラスター数とする方法のことをElbow method と言います。
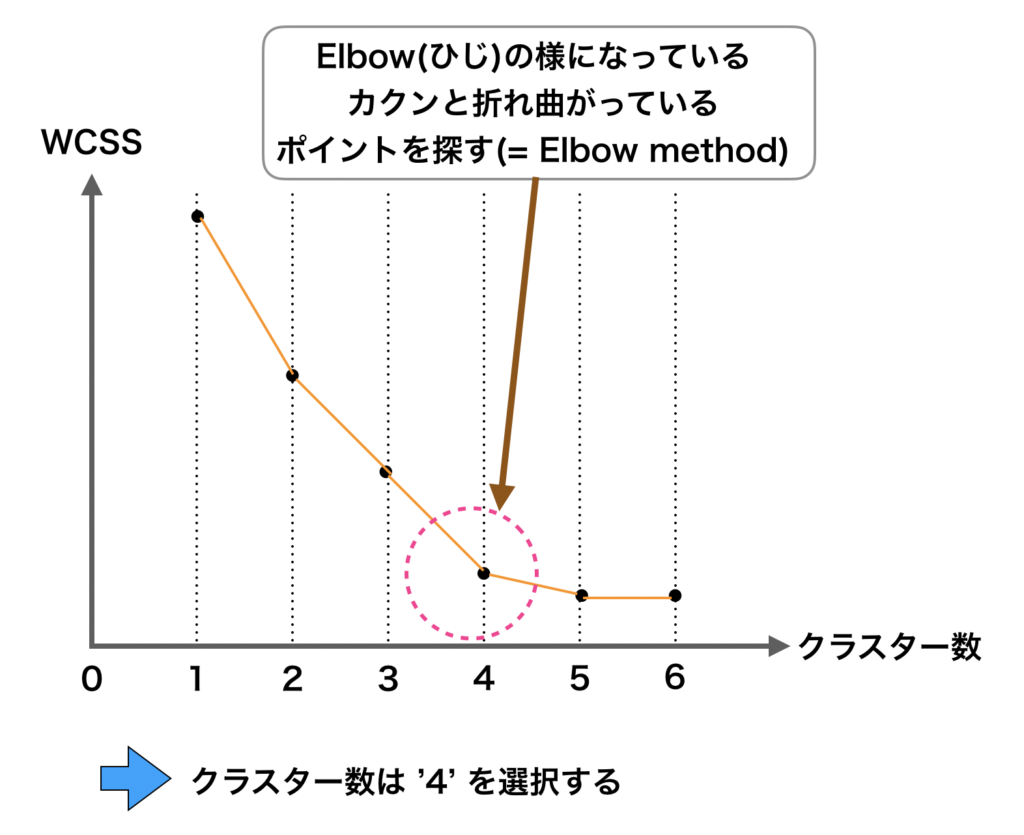 グラフを見ると、WCSSはクラスター数を増やせば増やすほど減少していっている。
グラフを見ると、WCSSはクラスター数を増やせば増やすほど減少していっている。
減少のペースを見ていくと、クラスター数が2個、3個、4個と小さい時にはWCSSは大きく減少するが、クラスター数が4個から増えてくるとWCSSの減少ペースが下がってくることがわかります。
すなわち、これ以上クラスター数を増やしてもWCSSは大して下がらないですよね。
このWCSSの現象ペースが急激に落ちている部分が最適なクラスター数であり、この部分を探す方法がElbow method です。
しかし現場で実装する際には、上図ではとても綺麗に曲がっているかと思いますが、実際にはこれほど綺麗に曲がることもないので、結構主観で決めることが多いのが実際のところです。
シルエットスコアとシルエットプロット
シルエットスコア
シルエットプロットという手法は「凝集性」と「分離性」の両方を考慮した手法です。
シルエットプロットを理解するためには、まず「シルエットコア」を理解する必要があります。
シルエットコアとは -1 〜 +1 の間をとる点数です。1に近いほど所属しているクラスターの中心に近く、かつその点数自身が所属しているクラスターを除いた他のクラスターから遠い場所にうちしていることを示しています。
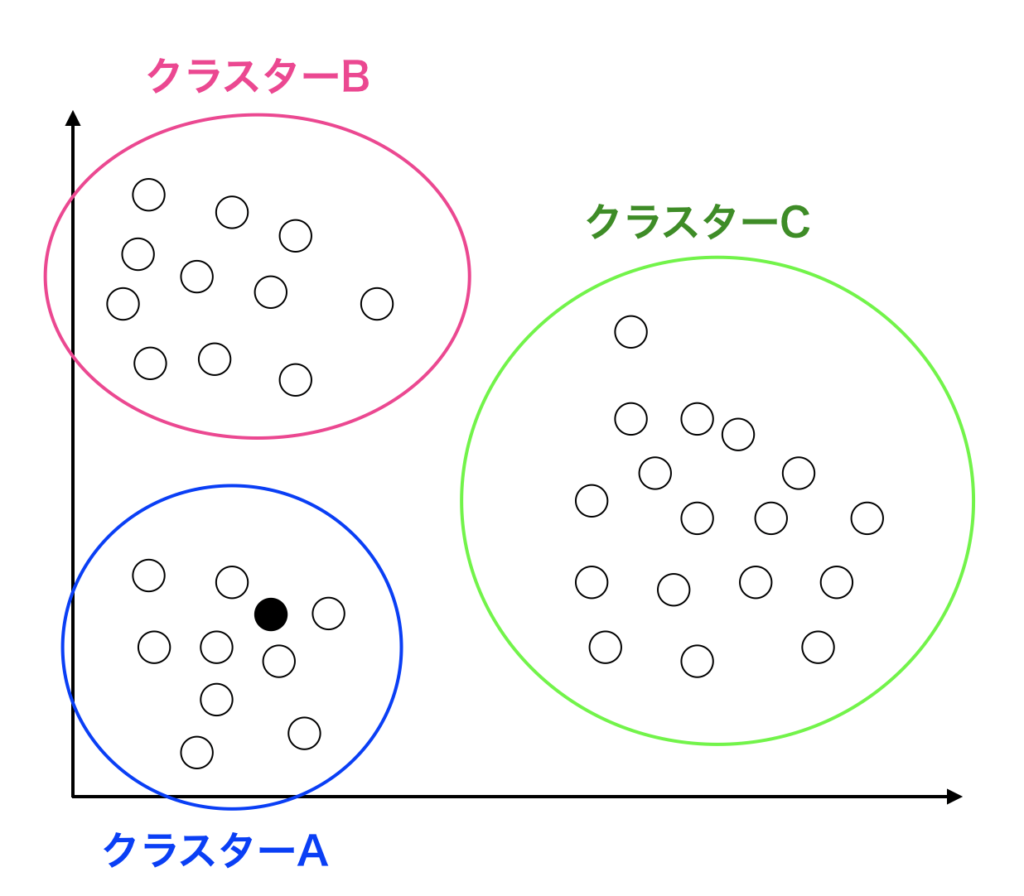
以下に示すのが、シルエットスコアの概略図です。
A, B, Cの3つのクラスターがあるとして、今調べたいのはAの中にある黒マル●のデータのシルエットスコアです。
この図を見て分かる様に、図の中にある黒マル●はクラスターAに所属しています。
またクラスターA以外で、この黒マル●に一番近いクラスターはクラスターBになります。
この黒マル●のシルエットスコアとは「クラスターAの方に近いのか、またはクラスターBに近いのか」ということをスコア化したものです。
すなわち、自分の所属するクラスターの中心に近いほど 1 になり、隣のクラスターであるBに近いほど -1 に近くなります。
クラスターAの中の1つの点(黒マル●)をデータ点 i とします。この点を例にとって解説します。
- ●からクラスターAの中の他の点までの距離の平均を算出し、その結果を $A(i)$ とします。
- また別のクラスターであるBとCの各々に含まれる点と、●との平均距離を算出します。各々の平均距離を $B(i)$ と $C(i)$ とします。
- $B(i)$ と $C(i)$ のうち小さい方を $B(i)$ とします。
- シルエットスコアの算出は次の様な式になります。
$$B(i) - A(i)/max( A(i), B(i))$$
この様になります。
シルエットプロット
上で解説した様に、それぞれの点でシルエットスコアを計算して可視化すると、以下の図の様になります。この図が示しているのが、シルエットプロットです。
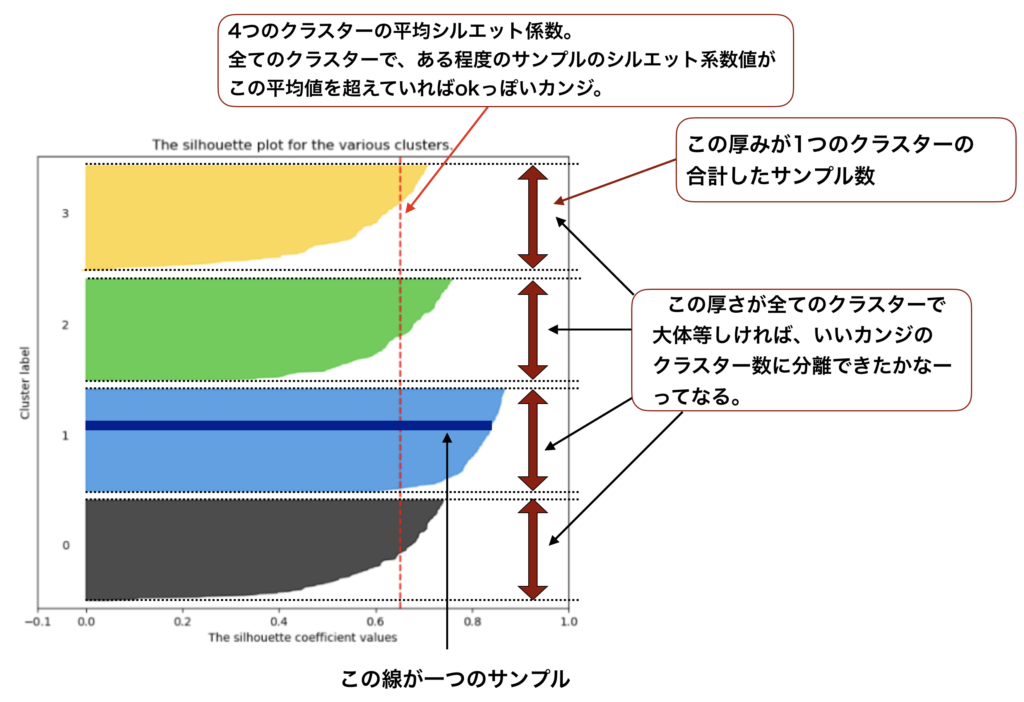
一見すると包丁が4つ並んでいる様に見えますが、これは横線がたくさん繋がってできているものなのです。
一つ一つの横線は各データの点のシルエットスコアです。
各々のクラスターのデータの点で計算したシルエットスコアを降順で並び替えて横線としてデータの数分だけ引いています。
そうすると、最初はクラスターの中心から距離の近いデータ点のシルエットスコア、すなわち1に近い横線が引かれるのですが、徐々に黒マル●が属するクラスターの中心から離れたデータの点のスコアの横線を引いていくことになります。
すなわち、シルエットスコアは徐々に下がっていくために包丁の様な形状として見えるわけです。
また、縦幅はそのままデータの点の数を表しているため、各々のクラスターにどれほどのデータが含まれているのかもシルエットプロットを見ればすぐに分かります。
まとめ|教師なし学習のクラスタリングについて

今回は機械学習のうち、教師なし学習のクラスタリングについての解説をしました。実際の実装方法についても今後追加して解説していきます。
まずは概論を掴んで、クラスタリングについて理解する様にしましょう。
今回は以上となります。
