
今回は "ベイズ統計学の事後分布を実際に計算する方法" についての内容になります。
ベイズの定理に関してはこの記事を参照していただければ幸いです。
-

ベイズ統計の理論と方法【初心者向け】
続きを見る
本記事の学習内容
- ベイズの定理の理解
- ベイズ統計学の流れの理解
- 事後分布を実際に計算できるようになる
では早速見ていきましょう。
ベイズの定理とは

まず、ベイズの定理の復習です。
式の各々のパーツの名称です。
$f(\theta | \mathcal{D})$:事後分布 (結果 ${D}$ が与えられた時の原因 $θ$ の条件付き確率 )
$f(\mathcal{D} | \theta)$:尤度関数 (カーネルと言います。原因( $D$ )と結果( $θ$ )を紐づけている部分)
$f(\theta)$: 事前分布 (原因についての事前知識の確率分布)
$f(\mathcal{D})$: エビデンス (事後分布の規格化定数)
上の式でもわかる様に、$f(\theta | \mathcal{D})$ (事後分布)は、$f(\mathcal{D} | \theta)$ (尤度関数)と$f(\theta)$ (事前分布)の積を$f(\mathcal{D})$ (エビデンス)で割って求める事が出来ます。
事後分布は結果( $D$ )が与えられた時に、原因( $θ$ )を求める確率の事でした。
ベイズ統計の流れ(袋の問題を例えにして)
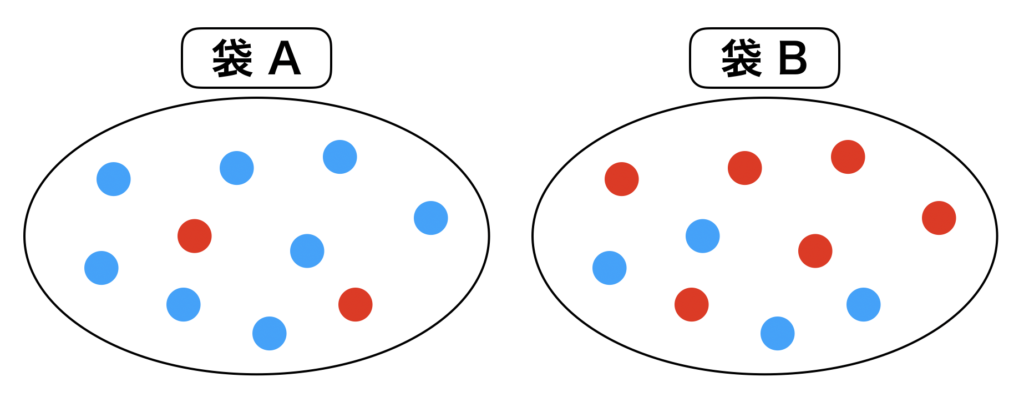
ベイズ統計の流れを、袋Aと袋Bの問題を例えにして進めていきましょう。
- 袋A 青; 8個 赤; 2個
- 袋B 青; 4個 赤; 6個
ベイズ統計の流れは以下の流れに沿って計算していきます。
- 下調べを行う。問題の背景を調べ流ことで、問題の原因と結果の関係の仮説を立てる。
- 統計モデルの作成を行う。下調べで得た情報に基づいて、統計のモデルを作る。
- 事後分布の計算を行う。得られているデータから、事後分布を推定する。
この3ステップを踏みます。
下調べ

下調べでは、問題の背景を調べて、原因と結果の関係の仮説を立てます。
- 袋A 青; 8個 赤; 2個
- 袋B 青; 4個 赤; 6個
この問題の背景
経験によると袋Aの方が大きく、掴みやすい。このためか、袋Aは袋Bよりも多く選ばれている。
また、それぞれの袋に赤玉、青玉が何個入っているのかを事前に知っている。
この様な背景がないかどうかを下調べを行う事により、調査します。
メモ
実際の統計モデルでは、この袋A,袋Bに何個の赤玉,青玉が入ってるかまでは分からない事がほとんどです。
そのため、これらは未知のパラメーターとして分布で調べる必要が出てきます。
統計モデルの作成

下調べで得た情報に基づいて、統計のモデルを作成していきます。
統計モデルを作成する過程で、尤度関数(カーネル)を決定する必要があります。
尤度関数
$\mathrm{p}(\mathrm{Y}=\mathrm{r} | \mathrm{X}=\mathrm{a})=0.2$
$\mathrm{p}(\mathrm{Y}=\mathrm{b} | \mathrm{X}=\mathrm{a})=0.8$
$\mathrm{p}(\mathrm{Y}=\mathrm{r} | \mathrm{X}=\mathrm{b})=0.6$
$\mathrm{p}(\mathrm{Y}=\mathrm{b} | \mathrm{X}=\mathrm{b})=0.4$
通常であれば、尤度関数は未知のものであるため、統計モデルを立てる事でどの様な分布に従うのかを仮説を立てつつ調べる事になります。
そのため、様々な分布を学習する必要があります。
背景として、事前確率が
$p(X=a)=0.7$
$p(X=b)=0.3$
と設定してみます。
事後分布の計算を行う。
得られたデータから、事後分布の計算を行いましょう。
ベイズの定理は以下の式になります。
$$f(\theta | \mathcal{D})=\frac{f(\mathcal{D} | \theta) f(\theta)}{f(\mathcal{D})}$$
まずはこのうち、$f(\mathcal{D} | \theta) f(\theta)$ の箇所のみの計算を行います。
※ $f(\mathcal{D})$ この箇所は最後に計算を行います。
今回は手動による計算を行いますが、通常では、MCMC(マルコフチェーンモンテカルロ法)を使用して事後分布の推定を行います。
設定
選ばれた袋から4回復元抽出を行い、結果は、{b, b, r ,b, }でした。
この設定を元に計算を行います。
$$p(x | y=b, b, r, b) \propto p(y=b, b, r, b | x) p(x)$$
ベイズの定理の分子のみ(右辺)に着目すると、上式の左辺と右辺が比例している事がわかります。
ここで、復元抽出は独立事象です。さらに、独立事象は積の和に変形する事ができるため、
$$p(y=b, b, r, b | x) p(x)=\prod_{i} p\left(y_{i} | x\right) p(x)$$
この式が成立します。
$\prod_{i}$ これは(パイ)と言い、各々の掛け算を意味します。
具体的には
$$\prod_{i} p\left(x_{i}\right)=p\left(x_{1}\right) p\left(x_{2}\right) p\left(x_{3}\right) \cdots p\left(x_{n}\right)$$
となります。
● $(X = A)$ の場合
先程の設定より、
$\mathrm{p}(\mathrm{Y}=\mathrm{r} | \mathrm{X}=\mathrm{a})=0.2$
$p(Y=b | X=a)=0.8$
$p(x=A)=0.7$
となるため、
$p(y=b, b, r, b | x) p(x)=\prod_{i} p\left(y_{i} | x\right) p(x)$
この式は
$p(x=A | y=b, b, r, b) \propto \frac{8}{10} \cdot \frac{8}{10} \cdot \frac{2}{10} \cdot \frac{8}{10} \cdot \frac{7}{10}=$
$ =0.7168 $ と計算できます。
● $(X = b)$ の場合
$p(Y=r | X=b)=0.6$
$p(Y=b | X=b)=0.4$
$p(x=B)=0.3$
となります。
そのため、
$p(y=b, b, r, b | x) p(x)=\prod_{i} p\left(y_{i} | x\right) p(x)$ この式を計算すると
$ =0.1152 $
と計算できます。
規格化
最終的に規格化(辻褄合わせ)を行います。
袋Aが選ばれた確率と袋Bが選ばれた確率は合計すると1にならなければいけません。
そうすると以下の式が成立します。
$p(x=A | y)+p(x=b | y)=1$ を用いれば、
$p(x=A | y=b, b, r, b)=\frac{0.7168}{0. 71687+0.1152} \cong 0.85$
$p(x=B | y=b, b, r, b)=\frac{0.1152}{0.7618+0.1152} \cong 0.12$
これらの式により {b,b,r,b} の玉を選んだ時には、袋A から選ばれた確率は 0.85 とわかります。
同様に、{b,b,r,b} の玉を選んだ時には、袋B から選ばれた確率は 0.12とわかります。
これらの0.85 や 0.12 を事後分布 と言います。
まとめ|ベイズ統計の理論と実際の計算方法

今回は以下のことを学びました。
本記事での学習内容のまとめ
- ベイズ統計学の計算過程の流れを学んだ。
- まず、問題の背景を把握して仮説を置く。
- 次に統計モデルを作成した後に、データから事後分布を推定する。
- ベイズ統計学の流れに沿って、袋の問題を通して実際に計算を行い、事後分布を算出した。
次回はベイズ更新を行い、事後分布の更新についての理解を深めていきます。
今回はこれでおわりとします。
