
今回の記事では、「ベイズ統計学」の基本的な内容に関して学習します。
前提として、「機械学習に必要な確率の基礎(事象・同時確率・条件付き確率)」についてや、「機械学習に必要な確率の基礎(期待値・分散)」についてを学習終えている方に向けた内容となっています。
少し自信のない方はこちらの記事も併せて読んでいただければと思います。
-

【機械学習に必要な確率の基礎】事象、同時確率、条件付き確率
続きを見る
-

【確率の基礎】期待値・分散について
続きを見る
本記事の内容
- ベイズ統計学の基本を理解する
- ベイズの定理を理解する
早速、見ていきましょう。
ベイズの定理とは

ベイズ推定とは
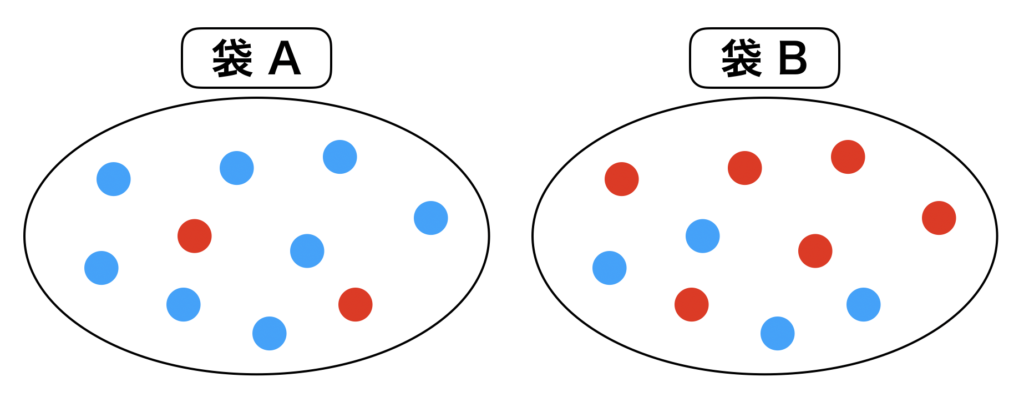
ここで袋A,袋Bがあると過程し、各々の袋に赤玉、青玉が入っているとしましょう。
袋 A には 2個の赤玉、8個の青玉が入っています。
また
袋 B には 6個の赤玉、4個の青玉が入っているとします。
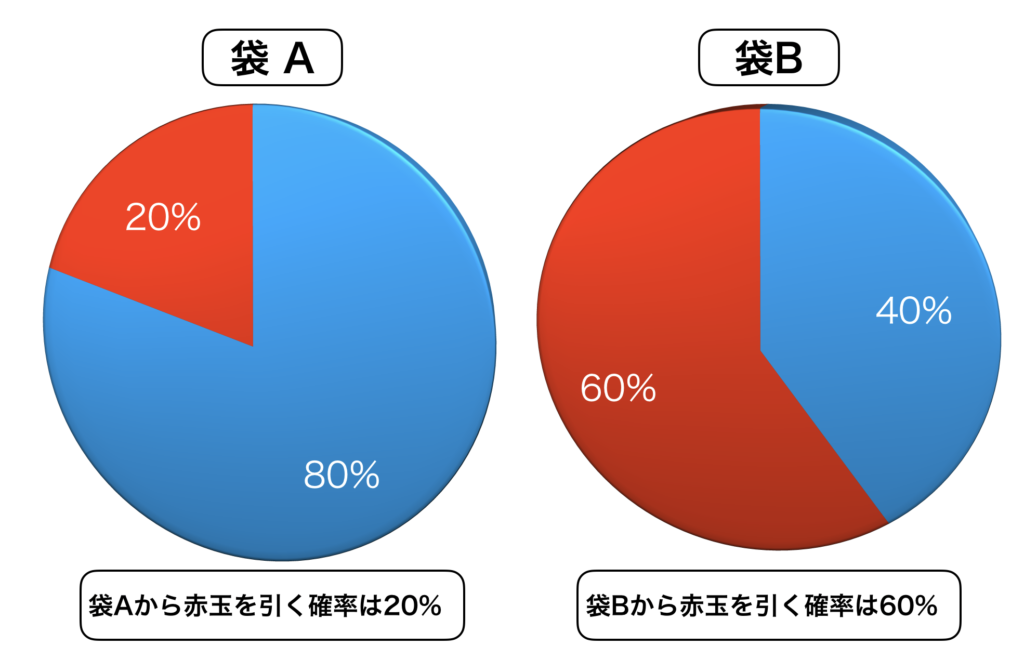
ここで条件付き確率 $p(Y|X)$ には袋と玉の相関情報が含まれています。
$Y$ :玉の選択
$X$ :袋の選択
を意味しています。
上の図を見たらわかる様に、袋ごとに赤玉、青玉を引く確率は異なります。
例えば、袋 A であれば、青玉を引く確率の方が高くなるわけですし、袋 B であれば、赤玉を引く確率の方が高くなるわけです。
すなわち、選んだ玉の情報と、袋の情報には相関性があります。
ここで、問題設定です。
選んだ袋がどちらか分からない状況で、袋から10回玉を取り出したとします。('復元抽出' と言います)
すると、以下の様な結果になりました。
赤玉: r
青玉: b
とします。
結果:r, b, b, r, b, b, r, b, b, r,
この様な結果となった時に、選んだ袋はどちらであったでしょうか。
選んだ玉の数を確認すると、青玉が多い様な感じになります。
推理してみてください。
すると、誰しもが青玉が出やすいのだから、青玉を引きやすい 袋A を選んだはずだ! と思われると思います。
この考え方の事を、
ベイズの考え方(ベイズ推定)= 出たデータ(結果)を元にして、袋(原因)を推定する。
と言います。
ベイズの定理の理論とは

>> Wikipediaより引用
ベイズの定理とは定理の名前にもなっているトーマス・ベイズさんが考えた定理です。
$\theta$ (原因) 選んだ袋
$D$ (結果) 出てくる玉
とします。
同時分布は条件付き確率を使って、以下の様に2通りに書くことができます。
$f$ は確率分布の事と考えてください。
特に下の式は、まずデータ $D$ が与えられた上で、データ $D$ の条件つきの下で原因 $\theta$ を考えるといったものです。
$f(\theta, \mathcal{D})=f(\mathcal{D} | \theta) f(\theta)$
$f(\theta, \mathcal{D})=f(\theta | \mathcal{D}) f(\mathcal{D})$
また、これらの2式を使用して式変形を行うと、
$f(\theta | \mathcal{D})=\frac{f(\mathcal{D} | \theta) f(\theta)}{f(\mathcal{D})}$
この様に式変形を行うことが出来ます。この式こそがベイズの定理となります。
ベイズの定理に関係する用語
もう一度ベイズの定理を記載しておきます。
$f(\theta | \mathcal{D})=\frac{f(\mathcal{D} | \theta) f(\theta)}{f(\mathcal{D})}$
ベイズの定理は各パーツに分類する事ができます。
すなわち、ベイズ統計学ではベイズ統計学に纏わる用語に意味が与えられています。
ベイズの式と、「事後分布」、「エビデンス」、「尤度関数」、「事後分布」の相関関係についておさえておきましょう。
ベイズの式からは、事後分布が3つのパーツに分けられる、という事がわかります。
$f(\theta | \mathcal{D})$ 事後分布:結果 $D$ (玉の色)が与えられた時の、原因 $\theta$ の条件付き確率。
$f(\mathcal{D} | \theta)$ 尤度関数(カーネル):原因と結果を紐づけしている部分のこと。(ベイズ統計の中枢とも言えます)
(例) 袋 Aを選んでいるなら青が出やすいし、袋 B を選べば赤が出やすい。という様に、原因と結果が紐づけられていることを意味します。
$f(\theta)$ 事前分布:原因についての事前知識の確率分布のこと。
(例) 袋の選べ方について、60%の確率で袋aを選んでいるらしい。いう様な事前の情報があった時に、 $f(θ)$ にその事前情報を調整する値を代入することができる。
$f(\mathcal{D})$ エビデンス:事後分布の規格化定数のこと。
事後分布の総和は 1 にならなければならないが、そのことに寄与するのが「エビデンス」、すなわち定数のこと。
演繹的な考え方(頻度論の立場)と帰納的な考え方(ベイズの立場)
演繹的な考え方(頻度論の立場)とは
$$f(\theta | \mathcal{D})=\frac{f(\mathcal{D} | \theta) f(\theta)}{f(\mathcal{D})}$$
再度ベイズの定理を見てみると、
「$f(\theta | \mathcal{D})$ (原因の確率)」と「$f(\mathcal{D} | \theta)$ (結果の確率)」が入れ替わっているのがわかります。
この $f(\theta | \mathcal{D})$ (原因の確率) のことを「逆確率」とも言います。
この様に、ベイズの定理とは真逆の考え方である、演繹的な(頻度論)考え方の立場では、「$θ$ (原因)があるから、$D$ (結果)が起こりうる」という考え方の立場をとります。
(例)袋Bを選んでいるのだから、赤が出やすい。という考え方。
帰納的な考え方(ベイズの立場)とは
$D$ (結果)があるから、$θ$ 原因が分かる。という考え方です。
演繹的な考え方とは真逆の考え方になります。
(例) 赤が出やすいということは、引いた袋は bなのではないか。という考え方。
ベイズの統計学が、従来の統計学と異なる点
従来の統計学の考え方
従来の統計学の考え方は、「 $θ$ (原因)は推定すべき定数(真の値)である」=「$θ$ は確率変数ではない」という考え方。
「信頼区間は、$θ$ が含まれるか、含まれないかの2択の区間である。」という考え方になる。
※ 95%信頼区間とは、100回中95回は真の値は信頼区間に入るが、5回は入らない、という考え方です。
また、$θ$はあくまで「推定すべき定数」であり、そもそも $θ$の確率分布自体がない、という立場をとっています。
したがって、事後分布の式 $f(θ|D)$ 自体考えられない、という立場をとります。
ベイズ統計学の立場
逆に、$θ$ は確率分布であり変数(確率変数)、すなわち定数ではないという考え方です。
ベイズ信頼区間は $θ$ が信頼区間の範囲に収まる確率ということで、信頼区間に関しても解釈がしやすい立場を取っています。
繰り返しになりますが、
$f(θ|D)$:$D$ (結果)が与えられた上で、$θ$ (原因)を予測するという意味の式のため、事後分布は $θ$の確率分布 という考え方です。
まとめ:ベイズ統計学の理論と方法

本記事の学習内容
- ベイズの考え方は、出た結果( $D$ )やデータを基に、その原因( $θ$ )を推定するというものである。
(例) 取った玉の色は赤色が多かったのだから、赤色の出やすい B を選んだはずだ。という考え方。 - ベイズの定理とは、尤度関数と事前分布、エビデンスから事後分布という逆確率を求める事である。
- パラメータ $θ$ の確率分布を考える事が出来るか、そうではないかという点で、ベイズ統計学と従来の統計学は異なる。
今回は以上となります。
皆様の知識のまとめになれば幸いです。
