この記事では、統計学となる基本統計量について解説していきます。
それでは、今回の記事のテーマです。
本記事の内容
- 母集団と標本
- 平均、中央値、分散、標準偏差について
- Pythonでの実装方法
比較的簡単な基本的内容からの学習となります。早速見ていきましょう。
母集団と標本の関係について
これから基本統計量の学習を始めますが、なぜこれらの知識が必要になるのか確認するところから始めましょ う。
例えば、庭の池の中にいる鯉の体⻑を調べたいとします。もし池の水を抜いて全ての鯉を捕まえることができれば(これを全数調査と言います)、鯉の体⻑やそのばらつきなどの情報を得ることができます。
しかし、池の水を全て抜くという作業はあまりにも労力が大きく、現実的ではありません。この例の鯉の数の様に、何かの集団のことを知りたいと思った時、どの様にすれば良いのでしょうか。
そのための考え方として「集団から一部のみを抽出(標本調査)し、そこから集団の情報を推測する」 方法があります。
ここで用語について確認です。
この「調査したい集団」、ここでは池の中の鯉全体のことを母集団と言います。母集団から抽出した一部の鯉のことを標本と呼びます。取得したデータ(鯉)を整理・要約することを記述統計、また 標本(鯉)から母集団(池にいる全ての鯉)について推測することを推測統計と呼びます。この関係図を以下に示します。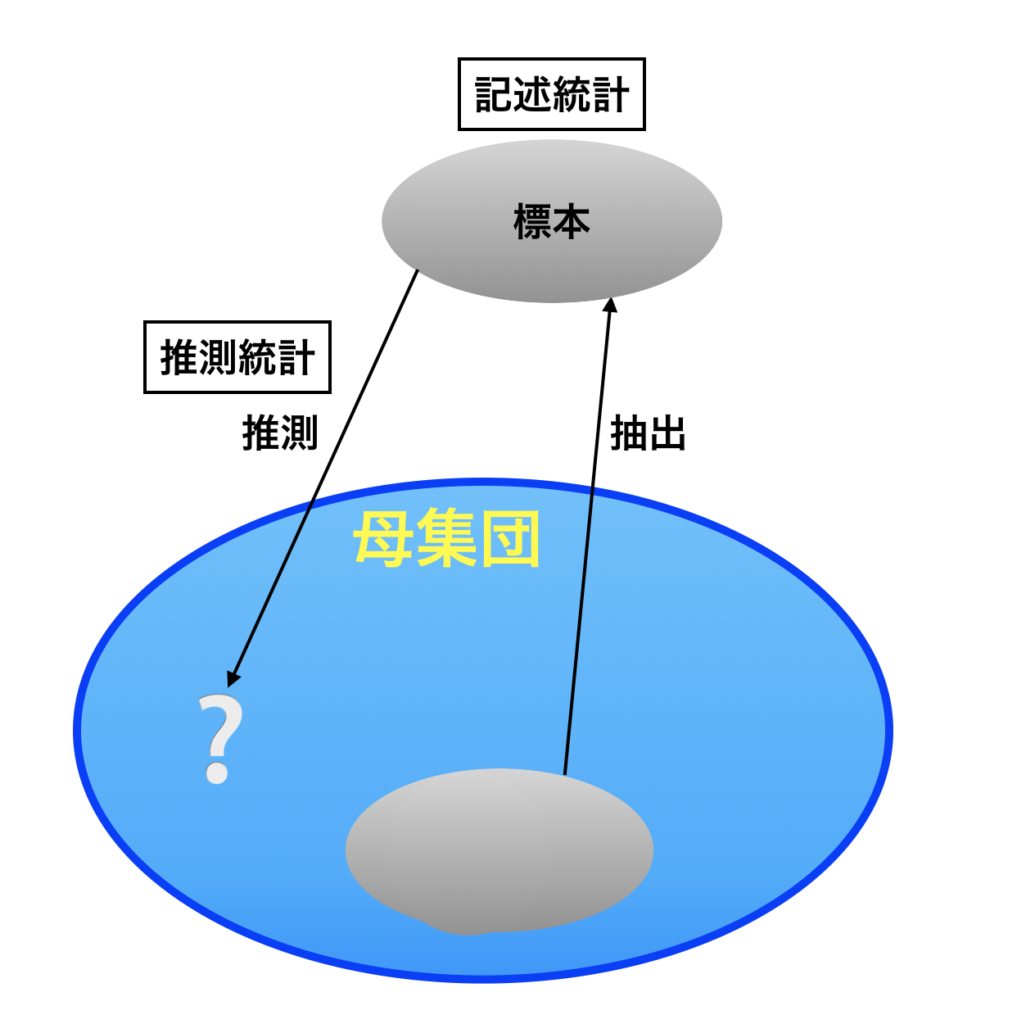
では、これからこの「推測」に必要となる知識を解説していきます。
平均値と中央値について
平均値
平均値は「全てのデータの値を足してデータ数で割ったもの」です。皆さんもよく使われるのではないでしょ うか。せっかくですので、ここではもう少し詳しい平均値の表記の仕方について学習しておきましょう。
統計学では多くの数値を扱いますので、この計算値が母集団から計算されたものなのか、それとも標本から計算さ れたものなのかを区別しておく必要があります。
母集団の平均 (母平均)
通常、母集団のデータ数を $N$ 、平均値を $μ$ で表します。母平均( $μ$ )は下記の計算式で計算できます。
$$\mu=\frac{1}{N} \sum_{i=1}^{N} x_{i}$$
標本の平均 (標本平均)
通常、標本のデータ数を $n$ 、平均値を $\bar{x}$ (エックスバー)で表します。このバーという記号は平均を表す際に使用されます。標本平均( $\bar{x}$ )は下記の計算式で計算できます。
$$\bar{x}=\frac{1}{n} \sum_{i=1}^{n} x_{i}$$
中央値 について
中央値は「データを小さい順に並べた場合、ちょうど中央にくるデータ」のことです。もしデータ数が奇数で あれば、中央値は 1 つのデータで決まります。
(例)5 匹の魚の体⻑データ:2cm, 3cm, 5cm, 7cm, 8cm →中央値は 5cm
しかしデータ数が偶数であった場合、ちょうど中央にくるデータというのは存在しません。その場合、中央に 最も近い 2 つのデータの平均を中央値とします。
(例)6 匹の鯉の体⻑データ:10cm, 5cm, 8cm, 6cm, 9cm, 7cm →中央値は 7.5cm (7cm と 8cm の平均)
この中央値を用いるメリットはその頑健性にあります。もし 5 匹の鯉のうち、1 匹だけ極端に大きな鯉がいた とします。もしかすると別種の鯉が混ざってしまったのか、または計測ミスがあったのかもしれません。
この ような値を外れ値と呼びます。平均値はこの外れ値に引きずられ大きなものになりますが、中央値は影響を受けにくく、変化をしない傾向があります。
分散と標準偏差について
分散とは
分散は「データがどの程度平均値の周りにばらついているか」を表す指標です。下記の図のように、各データ の値が散らばっているとします。この場合、ばらつきの大きさをどのように表現したら良いのでしょうか。
まず、全ての値から平均値を引いて、その平均を出してみましょう。そうするとプラスとマイナスが相殺され てしまい「ばらつきがゼロ」という結果になってしまいます。これでは正しくばらつきを表現できているとは 言えません。
次に、この各データと平均値の差を 2 乗してプラス・マイナスの符号を消してから平均を出してみましょう。 全てのデータが同じ値であれば分散は 0 になりますし、そうでなければ常に正の値となります。これが分散の 計算方法となります。平均値と各データの差のみを考えると、以下の様になります。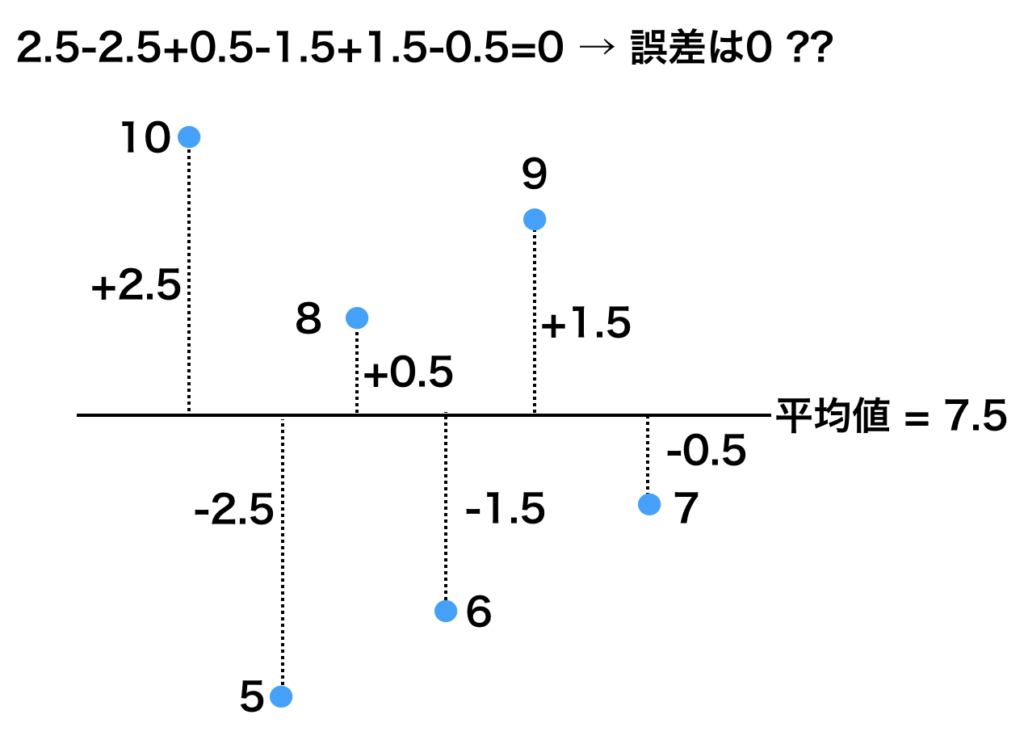
次に、この各データと平均値の差を 2 乗してプラス・マイナスの符号を消してから平均を出してみましょう。 全てのデータが同じ値であれば分散は 0 になりますし、そうでなければ常に正の値となります。これが分散の 計算方法となります。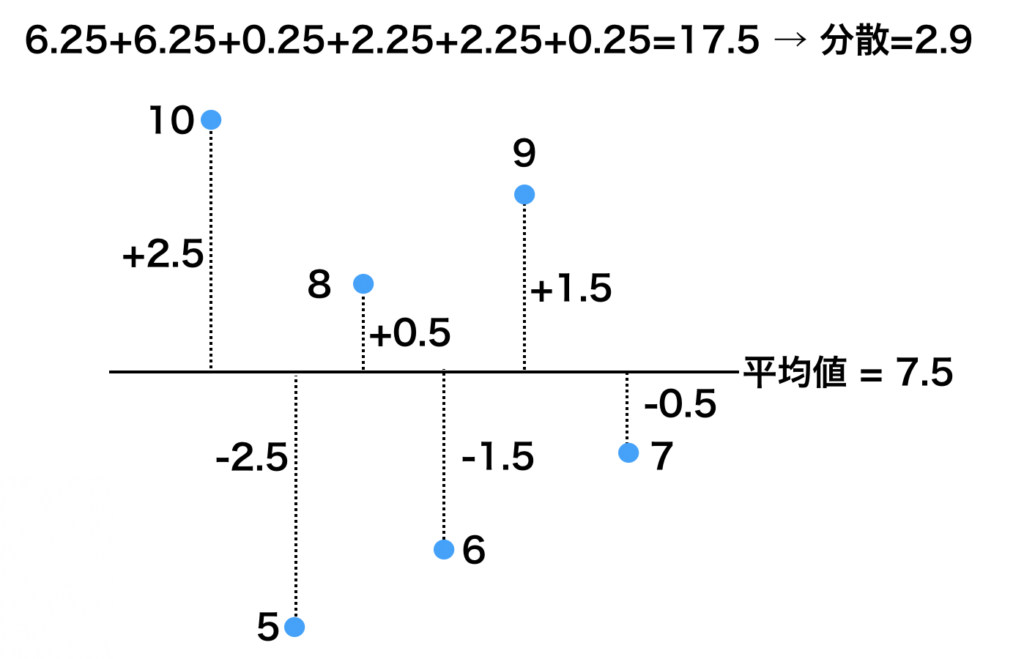
こちらも、母集団の分散と標本の分散で表記が違います。 母集団の分散(母分散): 母分散( $σ2$ )は下記の計算式で計算できます。
$$\sigma^{2}=\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}$$
標本の分散(標本分散): 標本分散(s2)は下記の計算式で計算できます。
$$s^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}$$
ここで注意が必要になります。実は、標本分散は母分散と比べて分散を過小評価してしまう問題 があります。
先ほどの図をもう一度よく見直してみましょう。分散は平均からの距離で計算していました。標本分散を計算する際には、母平均はわからないので標本平均を用いて計算していました。
上記の計算式でも $μ$ ではなく $x$ を用いていますね。そうすると、下記の図のように実際の平均からの距離(母平均からの距離)よりも短い距離で分散を計算してしまうことになります。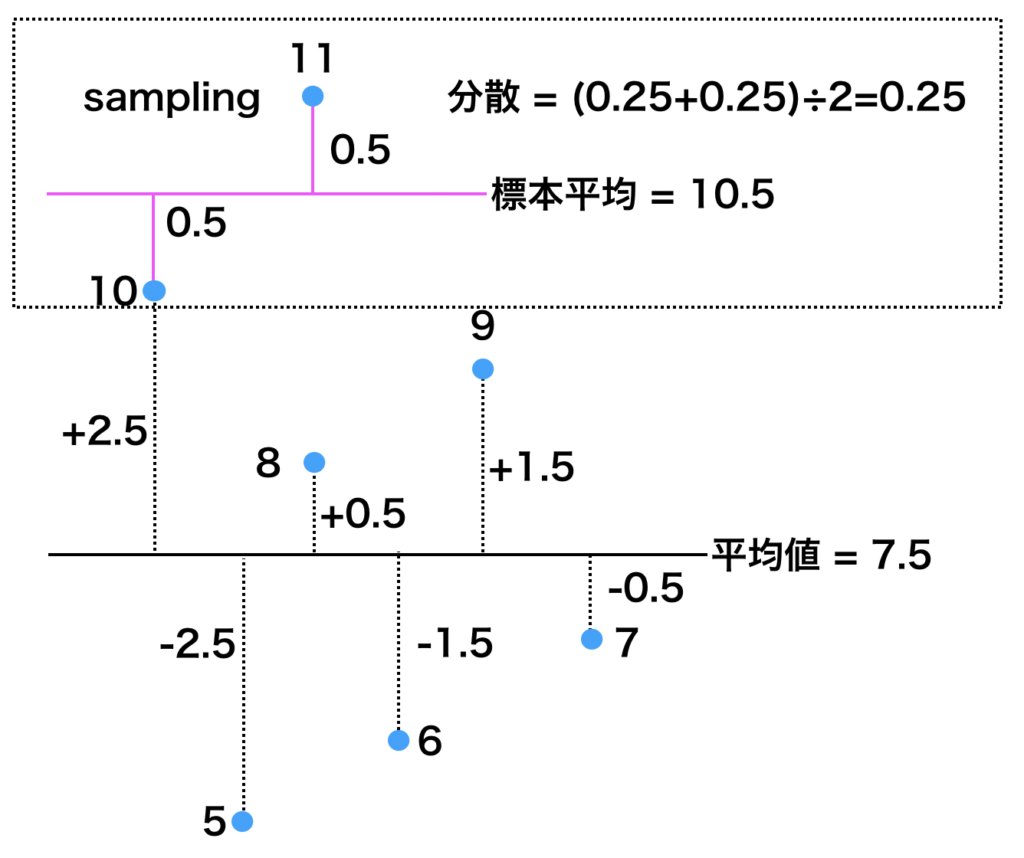
この問題を解決するのが不偏分散です。
不偏分散($\widehat{\boldsymbol{\sigma}}^{2}$)は下記の計算式で計算できます。このハットは推定値を表す際に使用されます。
$$\hat{\sigma}^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}$$
標準偏差
分散は「データがどの程度平均値の周りにばらついているか」を表す指標でした。しかし、プラス・マイナス の符号を消すために平均値からの距離を 2 乗しているため、計算された数字の単位は元のデータの単位と異な ります。魚の体⻑データが cm で記されていたとすると、分散の単位は cm2 となっています。これでは 1 匹あたり平均何 cm のばらつきがあるのか?という問いに答えることができません。
解決方法は、平方根をとることです。この分散の平方根をとったものを標準偏差といいます。これで単位を元 のデータと揃えることができました。それでは、計算式を確認しておきましょう。
母集団の標準偏差(母標準偏差):
$$\sigma=\sqrt{\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}}$$
標本の標準偏差(標本標準偏差):
$$s=\sqrt{\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}$$
不偏分散による標準偏差(不偏標準偏差):
$$\hat{\sigma}=\sqrt{\frac{1}{n-1} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}$$
これで単位を元のデータと揃えた状態でばらつきを表現することができます。
Pythonで実装
それでは、これまで学習した基本統計量の Python での計算方法をここで確認しておきましょう。もちろん上 記の計算式で計算できるのですが、Python には scipy という便利なパッケージがあります。こちらに数式が 格納されていますので、こちらの使い方を確認しておきましょう。
In
1 2 | import numpy as np import scipy as sp |
計算値が小数点を含む場合が多くあるかとおもいます。下記のコードを実行すると、表示される桁数が 3 桁になります。
In
1 | %precision 3 |
Out
1 | '%.3f' |
今回は 10 匹の鯉の体⻑データについて基本統計量を計算してみます。
In
1 | fish_data = np.array([10,5,8,6,7,7,5,9,5,4]) |
合計値
In
1 | sp.sum(fish_data) |
Out
66
平均値
In
1 | sp.mean(fish_data) |
Out
6.6
中央値
In
1 | sp.median (fish_data) |
Out
6.5
標本分散
In
1 | sp.var(fish_data, ddof=0) |
Out
3.44
不偏分散
In
1 | sp.var(fish_data, ddof=1) |
Out
3.82222222222222222222222
標本標準偏差
In
1 | sp.std(fish_data, ddof=0) |
Out
1.8547236990991407
不偏標準偏差
In
1 | sp.std(fish_data, ddof=1) |
Out
1.9550504398153572
まとめ
この記事では基本統計量の考え方と、その計算方法について学習しました。似たような計算式が何度も出て きたかもしれませんが、それぞれに意味があります。
その意味を追っていくと理解も深まるかと思います。皆さんが少しずつ統計の基礎とPythonの実装方法に慣れていける様な記事作りをしていきます。