こんにちは。産婦人科医のtommyです(Twitter:@obgyntommy)。
この記事では、住宅価格のデータセットを用いた教師あり機械学習の一通りの流れをscikit-learnを用いて学びます。
教師あり機械学習の一般的な流れは以下の通りです。
教師あり学習の機械学習の流れ
- データセットの読み込み
- データの前処理
- 探索的データ解析(EDA;Explanatory Data Analysis)
- 機械学習予測モデルの作成
- 性能評価
scikit-learnを用いた機械学習の流れについては、以下の記事を参照して下さい。
-

【機械学習】scikit-learnの使い方【基礎から全て解説】
続きを見る
又、Google Colaboratoryの使い方については以下の記事を参照して下さい。
-

Google Colaboratoryの使い方【完全マニュアル】
続きを見る
そのほか、教師あり学習の練習問題としては、ワインの品質判定、乳癌のデータセットを用いて行う問題や、糖尿病のデータセットを用いて行う練習問題も作成していますので、併せてどうぞ。
-

【教師あり学習】機械学習でワインの品質判定を行ってみよう【scikit-learn】
続きを見る
-

【教師あり学習】scikit-learn の乳がんデータセットで機械学習を行う
続きを見る
-

【教師あり学習】scikit-learnの糖尿病のデータセットで機械学習【回帰】
続きを見る
Google Colaboratoeyを使用して学習される方は、こちらのリンクを参照して下さい。
では早速学習していきましょう。
diabetesデータセットの読み込みと内容確認

skleanのライブラリから「fetch_california_housing」のデータセットを読み込みます。
fetch_california_housing のデータセットは、カリフォルニアの各地区の住宅築年数や部屋数などの住宅に関する平均スペックから、その地区の住宅の平均価格を予測するためのデータセットになります。
fetch_california_housing データセットの中身を確認します。
In[]
1 2 3 | from sklearn.datasets import fetch_california_housing data_california_housing = fetch_california_housing() data_california_housing |
Out[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | Downloading Cal. housing from https://ndownloader.figshare.com/files/5976036 to /root/scikit_learn_data {'DESCR': '.. _california_housing_dataset:\n\nCalifornia Housing dataset\n--------------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 20640\n\n :Number of Attributes: 8 numeric, predictive attributes and the target\n\n :Attribute Information:\n - MedInc median income in block\n - HouseAge median house age in block\n - AveRooms average number of rooms\n - AveBedrms average number of bedrooms\n - Population block population\n - AveOccup average house occupancy\n - Latitude house block latitude\n - Longitude house block longitude\n\n :Missing Attribute Values: None\n\nThis dataset was obtained from the StatLib repository.\nhttp://lib.stat.cmu.edu/datasets/\n\nThe target variable is the median house value for California districts.\n\nThis dataset was derived from the 1990 U.S. census, using one row per census\nblock group. A block group is the smallest geographical unit for which the U.S.\nCensus Bureau publishes sample data (a block group typically has a population\nof 600 to 3,000 people).\n\nIt can be downloaded/loaded using the\n:func:`sklearn.datasets.fetch_california_housing` function.\n\n.. topic:: References\n\n - Pace, R. Kelley and Ronald Barry, Sparse Spatial Autoregressions,\n Statistics and Probability Letters, 33 (1997) 291-297\n', 'data': array([[ 8.3252 , 41. , 6.98412698, ..., 2.55555556, 37.88 , -122.23 ], [ 8.3014 , 21. , 6.23813708, ..., 2.10984183, 37.86 , -122.22 ], [ 7.2574 , 52. , 8.28813559, ..., 2.80225989, 37.85 , -122.24 ], ..., [ 1.7 , 17. , 5.20554273, ..., 2.3256351 , 39.43 , -121.22 ], [ 1.8672 , 18. , 5.32951289, ..., 2.12320917, 39.43 , -121.32 ], [ 2.3886 , 16. , 5.25471698, ..., 2.61698113, 39.37 , -121.24 ]]), 'feature_names': ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude'], 'target': array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894])} |
このデータセットの中身はpythonの辞書型になっていますので、取得したい対象のキーを以下のように指定することによって対象の中身(バリュー)を取得できます。
以下は教師データの取得を行なっています。
In[]
1 | data_california_housing["target"] |
Out[]
1 | array([4.526, 3.585, 3.521, ..., 0.923, 0.847, 0.894]) |
データの前処理

次に、X を特徴量、y を教師データとして前処理を行なっていきます。
まずは教師データをpandasのデータフレームとしてまとめておきます。
教師データは浮動小数点数型で、『カルフォルニアの地区ごとの住宅価格平均』と捉えておけば良いでしょう。
In[]
1 2 3 | import pandas as pd y_all = pd.DataFrame(data_california_housing["target"],columns=["target"]) y_all.head() |
Out[]
1 2 3 4 5 6 | target 0 4.526 1 3.585 2 3.521 3 3.413 4 3.422 |
続いて、特徴量の前処理を行います。特徴量の名前は feature_names 、値は dataキー に含まれていますのでそれを用います。
In[]
1 2 | X_all = pd.DataFrame(data_california_housing["data"],columns=data_california_housing["feature_names"]) X_all.head() |
Out[]
1 2 3 4 5 6 | MedInc HouseAge AveRooms AveBedrms Population AveOccup Latitude Longitude 0 8.3252 41.0 6.984127 1.023810 322.0 2.555556 37.88 -122.23 1 8.3014 21.0 6.238137 0.971880 2401.0 2.109842 37.86 -122.22 2 7.2574 52.0 8.288136 1.073446 496.0 2.802260 37.85 -122.24 3 5.6431 52.0 5.817352 1.073059 558.0 2.547945 37.85 -122.25 4 3.8462 52.0 6.281853 1.081081 565.0 2.181467 37.85 -122.25 |
特徴量についてそれぞれは本記事では解説はしませんが、見た感じ、なんとなく築年数や部屋数など住宅価格に関係するであろう特徴量が含まれていることが分かります。
describeメソッドによって、一括で全ての特徴量の統計値の概要を表示できます。
In[]
1 | X_all.describe() |
Out[]
1 2 3 4 5 6 7 8 9 | MedInc HouseAge AveRooms AveBedrms Population AveOccup Latitude Longitude count 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 20640.000000 mean 3.870671 28.639486 5.429000 1.096675 1425.476744 3.070655 35.631861 -119.569704 std 1.899822 12.585558 2.474173 0.473911 1132.462122 10.386050 2.135952 2.003532 min 0.499900 1.000000 0.846154 0.333333 3.000000 0.692308 32.540000 -124.350000 25% 2.563400 18.000000 4.440716 1.006079 787.000000 2.429741 33.930000 -121.800000 50% 3.534800 29.000000 5.229129 1.048780 1166.000000 2.818116 34.260000 -118.490000 75% 4.743250 37.000000 6.052381 1.099526 1725.000000 3.282261 37.710000 -118.010000 max 15.000100 52.000000 141.909091 34.066667 35682.000000 1243.333333 41.950000 -114.310000 |
続いて、全てのデータを学習用と評価用に分割します。
これには sklearn の train_test_splitメソッド を使います。
学習用データと評価用データの数の割合ですが、今回は4:1とします。
※ 4:1でなければならないというわけではなく、一般的には評価用データ数が全体の2-4割程度にすることが多いです。
In[]
1 2 | from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X_all, y_all, test_size=0.2, random_state=0) |
学習データの特徴量と正解ラベルを1つのデータセットとしてまとめます。
In[]
1 | train = pd.concat([X_train,y_train],axis=1,sort=False) |
続いて、学習用データセットの特徴量と正解ラベルの型を確認します。pandas の infoメソッド により全てのカラムの型を確認できます。
In[]
1 | train.info() |
Out[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | <class 'pandas.core.frame.DataFrame'> Int64Index: 16512 entries, 12069 to 2732 Data columns (total 9 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 MedInc 16512 non-null float64 1 HouseAge 16512 non-null float64 2 AveRooms 16512 non-null float64 3 AveBedrms 16512 non-null float64 4 Population 16512 non-null float64 5 AveOccup 16512 non-null float64 6 Latitude 16512 non-null float64 7 Longitude 16512 non-null float64 8 target 16512 non-null float64 dtypes: float64(9) memory usage: 1.3 MB |
欠損値は無く、全ての特徴量が浮動小数点数(float型)ということが確認できていますね。
探索的データ解析(EDA)

続いて、このデータに関して探索的データ解析(EDA)を行なっていきます。
探索的データ解析(EDA)の目的ですが、これから機械学習を使って分類を行なっていきますが、その前に『回帰モデルによる予測が可能そうかそうでないか』を見極めるのが重要となります。
回帰モデルが有効かを見定めるにはまず教師データと各特徴量の相関を見るのが有効です。
相関(逆相関)が高い特徴量が存在するかをまずは確認してみましょう。
まず、相関を見るための相関係数の算出ですが、pandasの corrメソッド により一括で算出できます。
In[]
1 | train.corr() |
Out[]
1 2 3 4 5 6 7 8 9 10 | MedInc HouseAge AveRooms AveBedrms Population AveOccup Latitude Longitude target MedInc 1.000000 -0.115757 0.322014 -0.059645 0.004533 0.000858 -0.081245 -0.015081 0.692758 HouseAge -0.115757 1.000000 -0.146195 -0.071526 -0.298908 0.012472 0.016348 -0.113274 0.106470 AveRooms 0.322014 -0.146195 1.000000 0.853632 -0.066899 0.002975 0.101051 -0.024393 0.154426 AveBedrms -0.059645 -0.071526 0.853632 1.000000 -0.060918 -0.003718 0.066697 0.014037 -0.044415 Population 0.004533 -0.298908 -0.066899 -0.060918 1.000000 0.072710 -0.114819 0.105128 -0.027053 AveOccup 0.000858 0.012472 0.002975 -0.003718 0.072710 1.000000 -0.004679 0.013487 -0.033169 Latitude -0.081245 0.016348 0.101051 0.066697 -0.114819 -0.004679 1.000000 -0.924889 -0.142702 Longitude -0.015081 -0.113274 -0.024393 0.014037 0.105128 0.013487 -0.924889 1.000000 -0.047277 target 0.692758 0.106470 0.154426 -0.044415 -0.027053 -0.033169 -0.142702 -0.047277 1.000000 |
縦と横が交差するところが相関係数になります。
ただ、数値のみだと見辛いのでヒートマップによる可視化が有効です。
seaborn の heatmapメソッド によりヒートマップが作成できます。
引数 annot を True にすることによってヒートマップのマスの中に相関係数を表示することができます。
引数 square はヒートマップを正方形。引数 cmap はヒートマップの色を指定します。
In[]
1 2 3 4 5 | import seaborn as sns import matplotlib.pyplot as plt plt.rcParams['figure.figsize'] = (20.0, 10.0) plt.rcParams['font.family'] = "serif" sns.heatmap(train.corr(), annot=True,square=True, cmap='coolwarm') |
Out[]
1 2 3 | /usr/local/lib/python3.6/dist-packages/statsmodels/tools/_testing.py:19: FutureWarning: pandas.util.testing is deprecated. Use the functions in the public API at pandas.testing instead. import pandas.util.testing as tm <matplotlib.axes._subplots.AxesSubplot at 0x7f2b1dea10f0> |
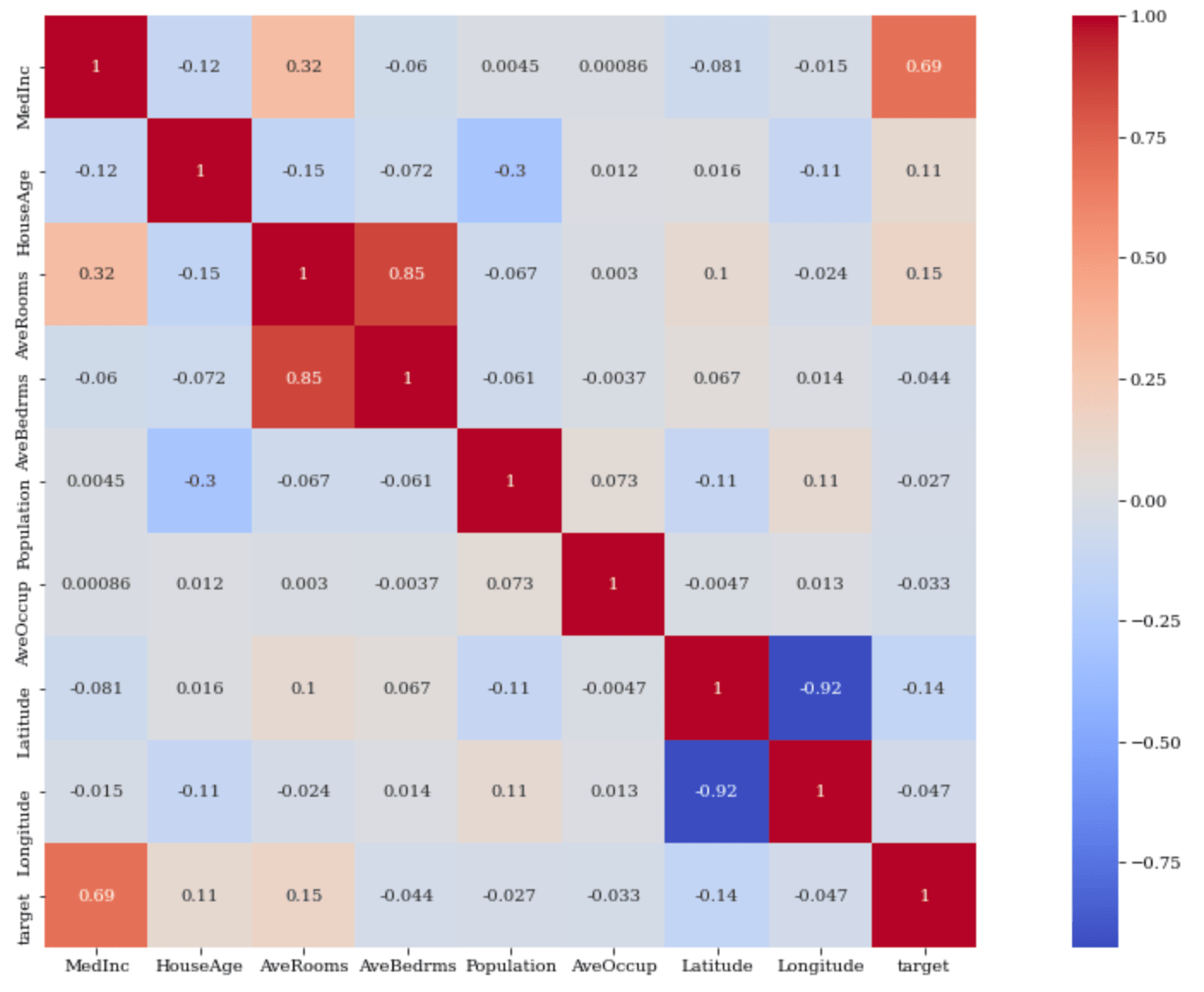
相関係数については、
- 0.7以上が相関が強い(マイナスの場合は-0.7以下が逆相関が強い)
- 0.4〜0.6はまあまあ相関が強い(マイナスの場合は-0.6〜-0.4 が逆相関が強い)
という目安で良いかと思います。(厳密には違いますが)
targetとの相関(逆相関)を確認したいので、target 列に注目します。
target は MedInc(その地区の人の収入)と相関が強く、その他の特徴量とはそこまで相関が強くないことがわかります。
それでは target と MedInc とのデータの関連性を散布図によって確認しておきましょう。
In[]
1 | sns.scatterplot( x='MedInc', y="target", data=train) |
Out[]
1 | <matplotlib.axes._subplots.AxesSubplot at 0x7f2b1e00e2e8> |

相関は見て取れますが、どうやらtargetの値の最大値が5になっていて、targetの値が5のデータ数が多いように見えます。
データの背景がわかりませんが違和感がありますよね。
もし5以上の値がまるめられて5になっているとすれば、このままモデルを作成するとあまり精度が得られない結果になるかもしれません。
一旦targetが5になるデータの全体に占める割合と、それらを除いたデータセットを作成しておきましょう。
In[]
1 2 3 4 5 | print("targetの値が5のデータは全データの",train[train["target"] ==5].shape[0]*100/train.shape[0],"%") train_2 = train[train["target"] <5] X_train_2 = train_2.drop("target",axis=1) y_train_2 = train_2[["target"]] sns.scatterplot( x='MedInc', y="target", data=train_2) |
Out[]
1 2 | targetの値が5のデータは全データの 0.13929263565891473 % <matplotlib.axes._subplots.AxesSubplot at 0x7f2b1609c978> |
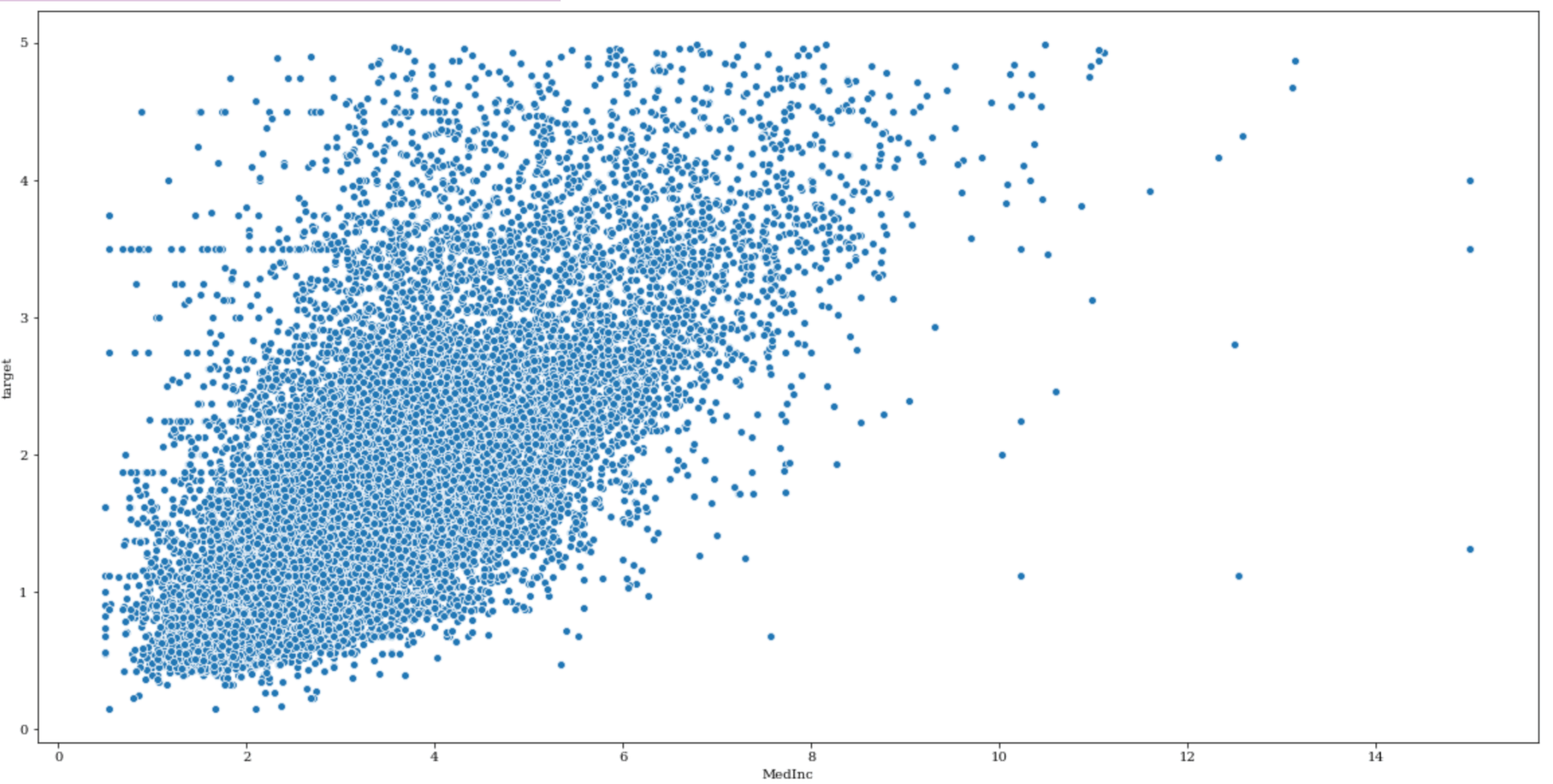
このtargetの値が5のデータは全体の0.14%くらいですので、そこまで全体としての割合は大きくありません。ただ、違和感があり結果にどう影響を及ぼすのか知りたいところです。
このように、違和感があるデータが予測精度にどのように影響を及ぼすか分からない場合、機械学習モデル作成の際に行う交差検定での精度スコアを比較することによって評価が行えます。
- target=5のデータを省かない
- target=5のデータを省く
それぞれについて交差検定内での精度スコアを比較してみましょう。
機械学習予測モデルの作成

機械学習予測モデルの作成を行います。交差検定を用いた、機械学習モデルのハイパーパラメータ探索から行います。
機械学習モデルとして①②両方ともElasticNetを用います。
ElasticNetの説明は割愛しますが、いわば従来のLasso回帰とRidge回帰のいいところどりをし、より過学習を防ぎやすいモデルと言ってよいでしょう。
-
ElasticNet — scikit-learn 1.8.0 documentation
続きを見る
ハイパーパラメータ探索としてグリッドサーチを用います。両方ともsklearnのクラスとして用意されています。
In[]
1 2 | from sklearn.linear_model import ElasticNet from sklearn.model_selection import GridSearchCV |
ElasticNetについては公式ドキュメントを確認しましょう。
今回はハイパーパラメータの候補として"alpha"と"l1_ratio"を取り上げます。
alphaは学習率、すなわち学習を進ませるスピードです。
大きいと計算が発散しますので一般的には出来るだけ小さくします。
l1_ratio はL1正則化の割合ですが、これはあまり意識することなく割合なので0-1の間の数を設定しておけば大丈夫です。
① target=5のデータを省かない場合
①の場合の交差検定を用いたグリッドサーチを行います。
In[]
1 2 3 4 5 6 7 8 9 | param_grid = {'alpha': [0.00001, 0.0001, 0.001,0.01, 0.01, 0.1],'l1_ratio': [0, 0.25, 0.5, 0.75, 1]} reg_1 = GridSearchCV(estimator=ElasticNet(), param_grid = param_grid, scoring="r2", cv = 5, n_jobs = -1) reg_1.fit(X_train,y_train["target"].values) |
Out[]
1 2 3 4 5 6 7 8 9 10 11 12 13 | /usr/local/lib/python3.6/dist-packages/sklearn/linear_model/_coordinate_descent.py:476: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations. Duality gap: 4388.9416321499575, tolerance: 2.209919021461081 positive) GridSearchCV(cv=5, error_score=nan, estimator=ElasticNet(alpha=1.0, copy_X=True, fit_intercept=True, l1_ratio=0.5, max_iter=1000, normalize=False, positive=False, precompute=False, random_state=None, selection='cyclic', tol=0.0001, warm_start=False), iid='deprecated', n_jobs=-1, param_grid={'alpha': [1e-05, 0.0001, 0.001, 0.01, 0.01, 0.1], 'l1_ratio': [0, 0.25, 0.5, 0.75, 1]}, pre_dispatch='2*n_jobs', refit=True, return_train_score=False, scoring='r2', verbose=0) |
交差検定での決定係数の結果を確認しましょう。
In[]
1 | print("Best Model Score: ",reg_1.best_score_) |
Out[]
1 | Best Model Score: 0.6057550185807385 |
約0.6という結果になりました。
② target=5のデータを省く場合
② の場合の交差検定を用いたグリッドサーチを行います。
In[]
1 2 3 4 5 6 7 | reg_2 = GridSearchCV(estimator=ElasticNet(), param_grid = param_grid, scoring="r2", cv = 5, n_jobs = -1) reg_2.fit(X_train_2,y_train_2["target"].values) |
Out[]
1 2 3 4 5 6 7 8 9 10 11 | GridSearchCV(cv=5, error_score=nan, estimator=ElasticNet(alpha=1.0, copy_X=True, fit_intercept=True, l1_ratio=0.5, max_iter=1000, normalize=False, positive=False, precompute=False, random_state=None, selection='cyclic', tol=0.0001, warm_start=False), iid='deprecated', n_jobs=-1, param_grid={'alpha': [1e-05, 0.0001, 0.001, 0.01, 0.01, 0.1], 'l1_ratio': [0, 0.25, 0.5, 0.75, 1]}, pre_dispatch='2*n_jobs', refit=True, return_train_score=False, scoring='r2', verbose=0) |
In[]
1 | print("Best Model Score: ",reg_2.best_score_) |
Out[]
1 | Best Model Score: 0.5702461870321043 |
①と②の結果を比較すると①の方のモデルの方が性能が良いことがわかります。
データは一部違和感がありましたが、グリッドサーチ内の交差検定の結果を元にすると①の方が結果的に筋の良いモデルができている、ということになります。
ここで大事なことは、データに定性的な違和感を感じた時は交差検定により定量的な評価が可能、ということです。
ここでは結果より①のモデルを使うということで進めていきましょう。
このハイパーパラメータを採用した際のモデルは best_estimator_メソッド により作成が可能です。
In[]
1 | reg_best = reg_1.best_estimator_ |
性能評価

続いて、予測と性能評価を行いましょう。
今回は元々性能指標として設定していた決定係数に注目することにしましょう。 決定係数は sklearn.metrics の中の r2_score で計算できます。
In[]
1 2 3 4 | from sklearn.metrics import r2_score y_pred = reg_best.predict(X_test) print(r2_score(y_test, y_pred)) |
Out[]
1 | 0.5917621030501266 |
さて、気になるのは決定係数約0.6が精度として信頼がおけるものなのかということですが、この決定係数は相関係数の2乗です。
本記事ではあまり細かいことは考えずに、相関係数として捉えると大体0.8弱くらいになるので、大体良い予測モデルが出来ているのではと、超前向きに捉えています。
まとめ

この記事では住宅価格のデータセットを用いた教師あり機械学習の一通りの流れをscikit-learnを用いて学びました。
Google Colaboratoeyを使用して学習される方は、以下を参照して学習して下さい。
-
Google Colab
続きを見る
今回は以上となります。
