【Python】最小勾配法を実装するために画像に描出して損失関数の最小値を求める

機械学習エンジニアになりたい人

最小勾配法のPythonでの実装したいな。

この様な方に向けた記事になります。

前置ですが、機械学習アルゴリズム（予測モデルを作成する際のデータの準備の流れ）という記事で、「野球選手の年俸を予測する」というテーマについて学習しました。

【Freak】プロ野球選手の年俸ランキングからデータを抽出し、年俸と打率の相関関係を描図しました。(描画したグラフは以下のグラフになります。)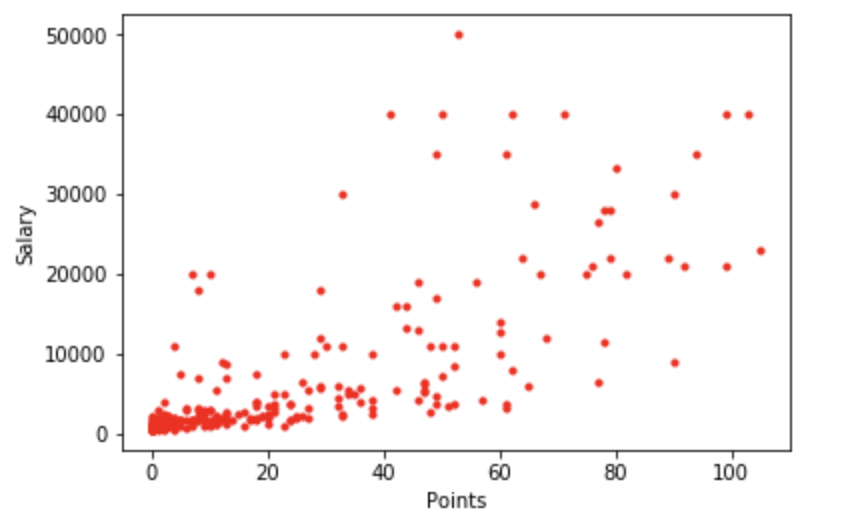

python プロ野球選手の年俸を予測する　機械学習
さらに、この散布図と線形モデルの相関関係を見い出すための工夫を行ないました。すなわち、この散布図が以下の様な線形モデルをとっているのではないか、と考えたわけです。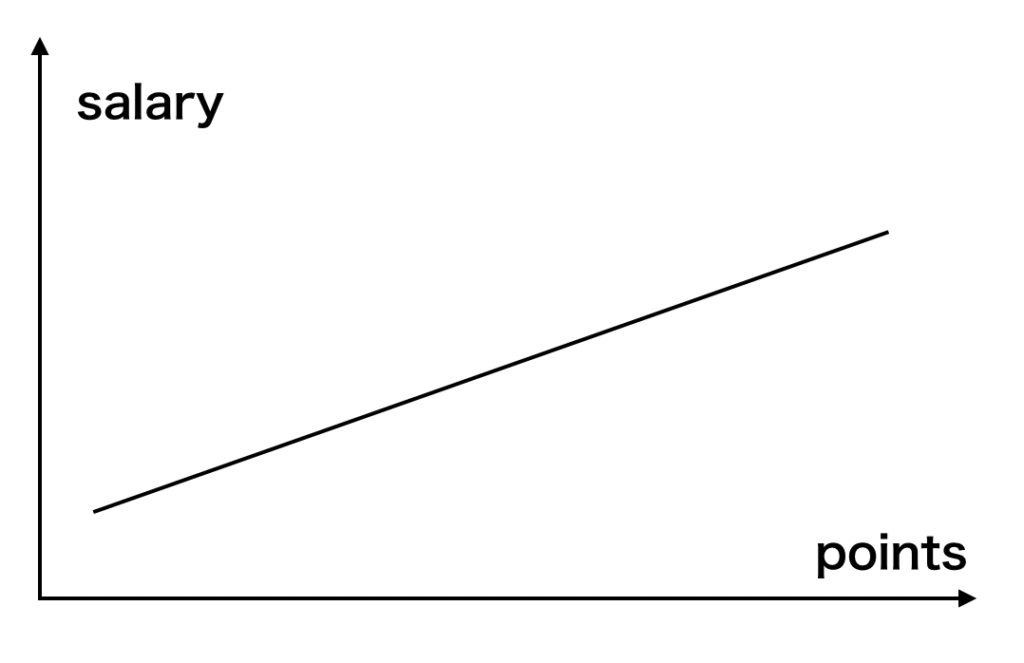
Python　線形モデル　最適化問題　評価関数　損失関数　機械学習この線形モデルの数式を以下の式で表すことが出来るとします。

$$S=a \times P+b$$

$S$ は年俸を、$P$ は打点を意味します。

そこで、「係数 $a$ と $b$ をどの様に決定すれば良いのか」が問題となってきます。

散布図に散在しているデータに合ったモデルをどのように見つければ良いか、というこの問題の事を最適化問題と言います。

最小化問題、最小二乗法については以下の記事を参照にしてください。

: 【Python】最適化問題を損失関数(評価関数)で解決する方法【機械学習入門】
続きを見る

: 【Python】単回帰分析と最小2乗法の求め方【機械学習入門】
続きを見る

さて、今回のテーマは最小勾配法を利用して $(a, b)$ の値を求めることです。

今回の記事で具体的に最小勾配法を使用して、損失関数(評価関数)の最小値をとる様な $(a, b)$ を求めましょう。

本記事の学習内容

最小勾配法をPythonで実装する手順を学ぶ
最小勾配法をPythonで実際に実装してみる
損失関数の最小値を、最小勾配法を用いて3Dグラフで描出する方法で求める

では早速みていきましょう。

最小勾配法の実装の手順

早速、最小勾配法の実装の手順について見ていきましょう。

グラフにプロットされている実際の値と線形モデルの差の最小値をとる $(a, b)$ を求める際には、以下の損失関数の式に着目しましょう。

$$\left(a^{*}, b^{*}\right)=\operatorname{argmin} D^{(2)}(a, b)$$

※ この式がイマイチ分からないという方は以下の記事にもう一度読んでみてください。

» 最適化問題を損失関数(評価関数)で解決する。

今からmatplotlibのmplot_3dを用いて、$D^{(2)}(a,b)$ を可視化する手順を示します。

この流れに沿って、jupyter notebookにコードを打ち込んで行ってみてください。

$D^{(2)}(a, b)$ を、dist(a, b)で定義する。
$a$ を変化させる。
$b$ を変化させる。
評価関数の値を計算する。
変数空間のメッシュ描図する。
$ X$ 軸に比例係数 $a$ を、$Y$ 軸に $y$ 切片 $b$ の値をとり、関数の値 $D$ (dist(a, b))を $z$ 軸にプロットする。

最小勾配法をPythonで実装する【実行あるのみ】

評価関数について

ここで、知識の整理を行いましょう。

線形モデル：$S=a \times P+b$
評価関数：$D^{(2)}(a, b)$
最小2乗法：$D^{(2)}(a, b)$を最小にする $(a, b)$ の組み合わせ $\left(a^{*}, b^{*}\right)$ を求める。
最適なモデル$S=a^{*} \times P+b^{*}$ を求めることを最小2乗法を求める。

ここで評価関数は次の式の様に表すことができます。

$$D^{(2)}(a, b)=\sum_{i=1}^{N}\left\{S_{i}-\left(a \times P_{i}-b\right)\right\}^{2}$$

最小勾配法をPythonで手順に沿って実行する

① 評価関数をコードで定義する【$D^{(2)}(a, b)$ を、`dist(a, b)`で定義する】

評価関数を$D^{(2)}(a, b)$の式で定義します。

ここでは関数distance(a, b, S, P)を用いてコードで定義していきます。

※ SとPの type はnumpy.ndarray です。

def distance(a, b, S, P):
    a = np.array(a).reshape((-1,1,1))
    b = np.array(b).reshape((1,-1,1))
    S = S.reshape((1,1,-1))
    P = P.reshape((1,1,-1))
    return ((S - (a*P + b))**2).sum(-1)

def distance(a, b, S, P):

a = np.array(a).reshape((-1,1,1))

b = np.array(b).reshape((1,-1,1))

S = S.reshape((1,1,-1))

P = P.reshape((1,1,-1))

return ((S - (a*P + b))**2).sum(-1)

※ ここで、配列をreshapeする際には、各次元にいくつ値を置くかを指定する必要があります。

例えば24個の値があった場合、$2×3×4$ や $1×2×12$ といった形に変形することができます。

上記コードの reshape の引数 (-1,1,1)ですが、2次元目に1列、3次元目に1列、-1と記載されることで、1次元目には残り全てを入れるという指定になります。

値の数が常に24個と決まっているのであれば (24,1,1) とすれば良いかと思いますが、関数の中などどのような長さの配列が入ってくるかわからない場合には「残り全て」としておいたほうが都合が良いのです。

※ また最後のコードのsum(-1)について解説します。

sum(-1) はどの次元について足し算をするか、という問題になります。

普通にsum()とすると、全ての値が足し算されますが、()の中に値を入れると指定した次元について足し算をすることができます。

足し算する前の配列は下記のようになります。

((S - (a*P + b))**2).shape
>> (500, 300, 241)

1 2	((S - (aP + b))*2).shape >> (500, 300, 241)

単純に((S - (a*P + b))**2).sum()と4034690850031601.5となりますが、次元の指定をすると下記のように出力結果が変わります。

((S - (a*P + b))**2).sum(0).shape
>> (300, 241)

((S - (a*P + b))**2).sum(1).shape
>> (400, 241)

((S - (a*P + b))**2).sum(2).shape
>>(400, 300)

((S - (a*P + b))**2).sum(-1).shape
>>(400, 300)

((S - (a*P + b))**2).sum(0).shape

>> (300, 241)

((S - (a*P + b))**2).sum(1).shape

>> (400, 241)

((S - (a*P + b))**2).sum(2).shape

>>(400, 300)

((S - (a*P + b))**2).sum(-1).shape

>>(400, 300)

sum(-1)は「最後の次元」という意味を持ちます。すなわち、sum(2)でも同じ結果が得られます。

② 定数 $a$ を変化させる

numpy.linspace()を用いて、0から1000の間で500個の値を定義し、定数aを変化させます。

numpy.linspace の使い方については以下の記事が参考になります。

» 【Samurai blog】【Numpy入門 np.linspace】等差数列の作成する関数

a = np.linspace(0, 1000, num=500)

1	a = np.linspace(0, 1000, num=500)

③ 定数 $b$ を変化させる

同様にbに、-10000から10000までの500個の値を入れてください。

b = np.linspace(-10000, 10000, num=300)

1	b = np.linspace(-10000, 10000, num=300)

④ 評価関数の値を計算する

上で作ったaとbの各組み合わせにおいて、メソッドdistance()を使用し、D.shape = (500, 500)となるような行列Dを作成します。

D = distance(a, b, salary, points)

1	D = distance(a, b, salary, points)

※ distanceですが、通常引数には2つの値を挿入して距離を算出するために使用します。

今回は実際のsalary(S)と予測したsalary(a*P + b)の距離を計算しています。

ただこの距離というのはa、bの値により変わりますので、a400個、b300個の値の組み合わせ（400x300）について全て S と a*P + b の距離を出しています。

下の⑦を確認していただきたいのですが、よってDのtypeの出力が 400x300 になっています。

⑤ 変数空間のメッシュを作る

aとbをメッシュ型で描図します。

A, B = np.meshgrid(a, b, indexing='ij')を使い、a, bの値に対応したメッシュをそれぞれA, Bに格納してください。

A, B = np.meshgrid(a, b, indexing='ij')

1	A, B = np.meshgrid(a, b, indexing='ij')

※ np.meshgrid の扱い方ですが、これは格子点を作成する上で重要なNumpyのメソッドになります。

以下のサイトでわかりやすく記載されていますので、参考にしてください。
» 【Numpy】格子点の作成

※ また、indexing='ij' についてですが、こちらは座標軸の指定を行うパラメータです。

今回の例ではAが400要素、Bが300要素ありますので「400x300または300x400」の行列が必要となります。

ここで meshgrid を使うのですが、もしindexing=‘ij’としますと400x300、indexing=‘xy’とすると300x400の配列が作成できます。

今回は、高さ情報にあたるnp.log10(D)が 400x300 の配列となっていますので、配列の形式を合わせるためにindexing=‘ij’を採用したということになります。

下記サイトの「indexing引数を指定」の項が参考になります。
» 配列の要素から格子列を生成するnumpy.meshgrid関数の使い方

⑥ $x$ 軸、$y$ 軸、$z$ 軸にプロットする

実際にプロットします。

3Dでメッシュ型のプロットとして描図してみましょう。
mpl_toolkits.mplot3dからAxes3Dをインポートして使います。
※ 詳しくはmplot3d tutorialを参照

プロット関数としてはAxes3D.plot_surface(A, B, np.log10(D), cmap=plt.get_cmap("viridis_r"))を使います。

Dの値そのままだと、値が大きすぎて変化が分かりづらいため、np.log10(D)で対数を取ります。
色マップは通常とは逆に、値が低いほど鮮やかな色になる方が見やすいでしょう。ここでは"viridis_r"を使っています。
見る角度はAxes3D.view_init(azim=<angle>, elev=<angle>)で調節できます。

In[]

from mpl_toolkits.mplot3d import Axes3D 

fig = plt.figure()
fig.set_size_inches(12, 8)
ax  = fig.add_subplot(111, projection='3d')  
ax.plot_surface(A, B, np.log10(D), cmap=plt.get_cmap("viridis_r"))

ax.set_title("$D^{(2)}(a,b)$")
ax.set_xlabel("$a$")
ax.set_ylabel("$b$")
ax.set_zlabel("$D$")
ax.set_yticks((-10000, -5000, 0, 5000, 10000))
ax.view_init(azim=-70, elev=20)
fig.savefig("images/linearmodel_paramsweep.png")
plt.show()

from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()

fig.set_size_inches(12, 8)

ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(A, B, np.log10(D), cmap=plt.get_cmap("viridis_r"))

ax.set_title("$D^{(2)}(a,b)$")

ax.set_xlabel("$a$")

ax.set_ylabel("$b$")

ax.set_zlabel("$D$")

ax.set_yticks((-10000, -5000, 0, 5000, 10000))

ax.view_init(azim=-70, elev=20)

fig.savefig("images/linearmodel_paramsweep.png")

plt.show()

※ add_subplot の引数の中の数字が何を表しているかは以下のサイトが参考になります。» subplot_add の引数の数字は何を表しているのか

ちなみにここの記載されているコードでは fig.add_subplot(111, projection='3d') とあります。

通常、subplot(a,b,c)は「作図エリアをa×bに分けたうちのc番目」という意味になります。

ここでは1×1に分けたうちの1つ目の作図エリア、ということになります。1つ目の作図エリアであれば、なんだか意味がなさそうに思えるのですが、3Dplotの際には必要となります。

※ fig.savefig("images/points_vs_salary_scatter.png")

このコードは「作成した図を points_vs_salary_scatter.png という名前でimagesフォルダに保存する」コードです。

savefig は matplotlib の関数ですので、matplotlib の公式サイトも参照してみてください。
また、Qiita にも参考になる記事がありますので併せてどうぞ。
» matplotlib で作図したプロットを画像ファイルに保存する方法

※ ax.plot_surface(A, B, np.log10(D), cmap=plt.get_cmap("viridis_r"))

この viridis_r はmatplotlibのカラーマップから色を取ってきています。

公式サイトに見本があります。

今回使った viridis は一番最初に出てくるカラーバーを改訂したものとなります。

色の指定では、‘blue’や‘red’のような一般名称も使えますが、このような名称のついた色を使うこともできます。
» matplotlib

このコードで描画された図は以下の様になります。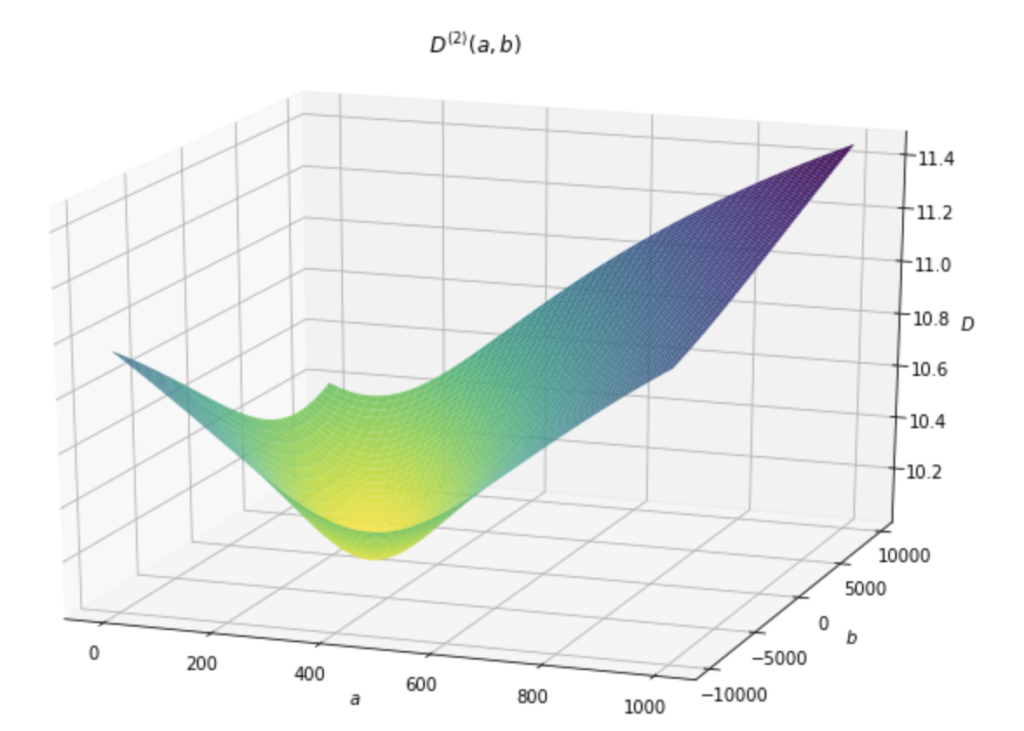最小勾配法　勾配法　最小値　python 機械学習　最小2乗法　実装

⑦ $A$のtype, ((S - (aP + b))*2) のtypeについて【補足】

ここで、Aのtype、((S - (a*P + b))**2) のtypeについて確認してみましょう。

Aのtype

# 入力
dataset = pd.read_csv("baseball_salary.csv")

points = np.array(dataset["打点"])
P = points.reshape((said 1,1,-1))

salary = np.array(dataset["推定年俸"])
S = salary.reshape((1,1,-1))

a = np.linspace(0, 900, num=400)
a = np.array(a).reshape((-1,1,1))

b = np.linspace(-10000, 10000, num=300)
b = np.array(b).reshape((1,-1,1))
D = distance(a, b, salary, points)
A, B = np.meshgrid(a, b, indexing='ij')

A.shape

# 出力
(400, 300)

# 入力

dataset = pd.read_csv("baseball_salary.csv")

points = np.array(dataset["打点"])

P = points.reshape((said 1,1,-1))

salary = np.array(dataset["推定年俸"])

S = salary.reshape((1,1,-1))

a = np.linspace(0, 900, num=400)

a = np.array(a).reshape((-1,1,1))

b = np.linspace(-10000, 10000, num=300)

b = np.array(b).reshape((1,-1,1))

D = distance(a, b, salary, points)

A, B = np.meshgrid(a, b, indexing='ij')

A.shape

# 出力

(400, 300)

Dのtype

# 入力

dataset = pd.read_csv("baseball_salary.csv")

points = np.array(dataset["打点"])
P = points.reshape((1,1,-1))

salary = np.array(dataset["推定年俸"])
S = salary.reshape((1,1,-1))

a = np.linspace(0, 900, num=400)
a = np.array(a).reshape((-1,1,1))

b = np.linspace(-10000, 10000, num=300)
b = np.array(b).reshape((1,-1,1))
D = distance(a, b, salary, points)
A, B = np.meshgrid(a, b, indexing='ij')

((S - (a*P + b))**2).sum(0).shape

# 出力
(300, 241)

# 入力

dataset = pd.read_csv("baseball_salary.csv")

points = np.array(dataset["打点"])

P = points.reshape((1,1,-1))

salary = np.array(dataset["推定年俸"])

S = salary.reshape((1,1,-1))

a = np.linspace(0, 900, num=400)

a = np.array(a).reshape((-1,1,1))

b = np.linspace(-10000, 10000, num=300)

b = np.array(b).reshape((1,-1,1))

D = distance(a, b, salary, points)

A, B = np.meshgrid(a, b, indexing='ij')

((S - (a*P + b))**2).sum(0).shape

# 出力

(300, 241)

まとめ

損失関数の最小値を、最小勾配法を用いて「3Dグラフで描出する」方法で求めてみました。

$(a, b)$ の組み合わせに対応した損失関数 $D^{(2)}(a, b)$ をグラデーションで表現しています。

$a = 280, b = 0$ 付近に最小値がありそうだなということがわかります。

今回は3d画像で描図することで最小値の場所を大体求めることができましたが、更に正確に求める方法について考えていきましょう。

【Python】最小勾配法を実装するために画像に描出して損失関数の最小値を求める

【Python】最適化問題を損失関数(評価関数)で解決する方法【機械学習入門】

【Python】単回帰分析と最小2乗法の求め方【機械学習入門】

最小勾配法の実装の手順

最小勾配法をPythonで実装する【実行あるのみ】

評価関数について

最小勾配法をPythonで手順に沿って実行する

① 評価関数をコードで定義する【\(D^{(2)}(a, b)\) を、dist(a, b)で定義する】

② 定数 $a$ を変化させる

③ 定数 $b$ を変化させる

④ 評価関数の値を計算する

⑤ 変数空間のメッシュを作る

⑥ $x$ 軸、$y$ 軸、$z$ 軸にプロットする

⑦ $A$のtype, ((S - (aP + b))*2) のtypeについて【補足】

まとめ

① 評価関数をコードで定義する【\(D^{(2)}(a, b)\) を、`dist(a, b)`で定義する】