なるべく教材を購入せず、サイトに掲載されているものだけで効率よく勉強したいです。
この様な方に対する記事になります。
この記事では、scikit-learnを使用して機械学習アルゴリズム(予測モデル)を作成し、さらにデータ分析に至るまでの流れについて1から解説していきます。
機械学習をなるべくコンパクトに最短で学ぶための知識をまとめました。機械学習アルゴリズムにおいてデータを分析する流れを下の図で示します。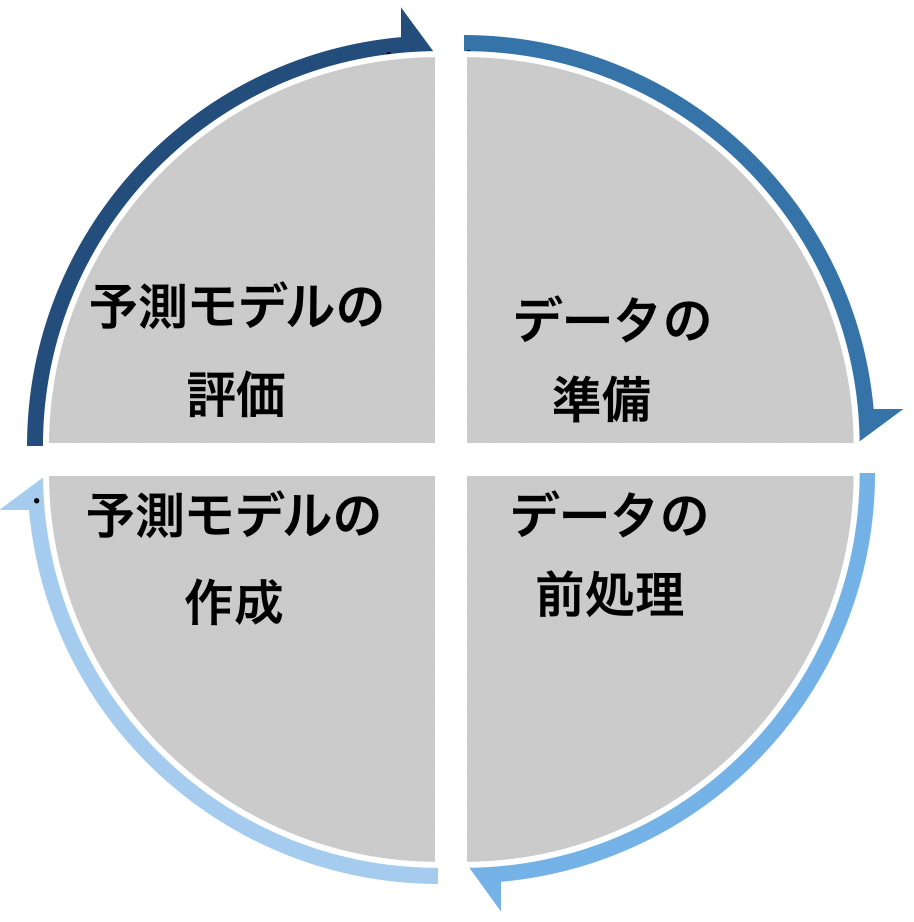
まとめると、データ分析を行う流れとしては以下の様な流れになります。
機械学習でデータ解析を行う流れ
- データの準備
- データの前処理
- (機械学習アルゴリズム)予測モデルの作成
- (機械学習アルゴリズム)予測モデルの評価
これらのステップの流れに沿って解説していきます。
データの準備
まずはデータの準備を行う必要があります。データの準備に関しては「プロ野球選手の年俸と打率」の関係を出すためにプロ野球データFreakより必要なデータを抽出してcsv形式のファイルで保存します。
具体的なデータ作成までの方法の流れは以下の記事をどうぞ。
-
機械学習アルゴリズム（予測モデル）を作成する際のデータの準備の流れ
続きを見る
データの前処理
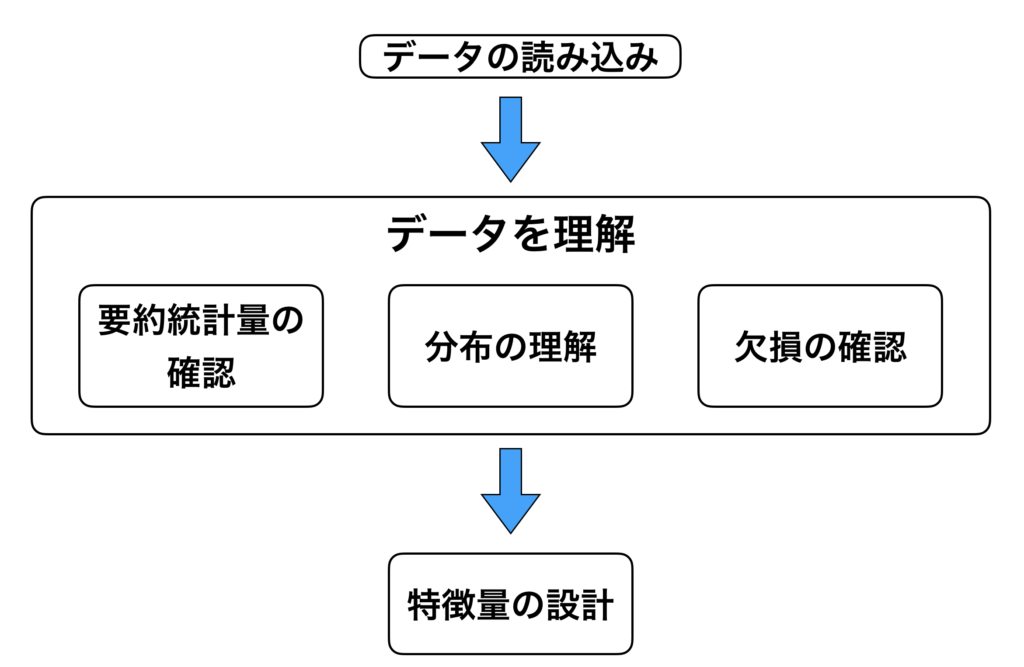
データ収集を行なった後はデータの前処理を行う必要があります。データの前処理は主に上の過程を経て行なっていきます。まとめると、以下の様なステップを踏んで処理を行います。
- 準備したデータの取り込みを行う。
準備した csv 形式の取り込みを行います。 - データの理解
次の工程として、「データの理解」をします。具体的には、カラムの定義や、欠損があるのか、ないのかなどの確認を行います。 - 特徴量の設定
データの理解が終了すれば、最後は「特徴量の設計」を行います。
データをそのまま使用しても良い結果に繋がらない場合があるので、新たに特徴量を作るなど色々と試してみる必要があります。
具体的なデータ前処理の方法は以下の記事をどうぞ。[kanren id="14250"]
機械学習アルゴリズム(予測モデル)の作成
さて、いよいよ機械学習のアルゴリズムにデータを投入して予測モデルを作成する過程に入ります。
機械学習には多くのアルゴリズムがありますので、この記事ではこのうちの以下の3つについて紹介します。
機械学習で押さえておくべアルゴリズム
- 線形回帰モデル(Linear Regression)
- 回帰木(Regression Tree)、決定木(Decision Tree)
- ランダムフォレスト(random Forest)
他にもアルゴリズムはあるのですが、まずはこの3つを重点的に学習しましょう。
機械学習アルゴリズムを理解する上での5つのポイント
機械学習アルゴリズムを理解する上では(特に教師あり学習のアルゴリズム)、以下の5つのポイントがあります。
- 予測したい対象の変数(ターゲット変数)：連続値やフラグ
- 目的関数
- 関数の形状
- ハイパーパラメーター
- モデルの解釈可能性と予測性能(精度)
この5つのポイントについて解説していきます。
予測したい対象の変数(ターゲット変数)
教師あり学習では、予測したい対象となる変数、すなわちターゲット変数というものがあります。
「プロ野球選手の年俸と打率」の関係でいうところの「プロ野球選手の年俸」ですね。
ちなみに「プロ野球選手の年俸と打率」は連続値です。
目的関数
目的関数とは、機械学習のアルゴリズムが何を最小化・最大化したいのかということを表現するための関数です。
線形回帰モデルの場合には、「予測した値と実際の値との差の2乗の合計(2乗誤差)」を最小化するために、「傾き」や「切片」を調整します。
この「予測した値と実際の値の差の2乗の全ての値の合計」に当たる概念が目的関数です。
全ての教師あり学習には目的関数があるため、「目的関数が何であるのか」を理解することが機械学習アルゴリズムを勉強する際の重要ポイントです。
関数の形状
関数の形状というのは、どの様にモデルが表されるか、ということを意味しています。
例えば、「野球選手の年俸と打率の関係」では「年俸 $S$ は打点$P$ に比例する」というモデルとして表現できます。具体的な関数としては、以下の式を表すことができます。
$$S=a \times P+b$$
ちなみにこのモデルは「線形モデル」と呼ばれ、線形モデルをデータにフィットさせる過程を「線形回帰」と呼びます。
この他にも回帰木というアルゴリズムは、関数の形がツリー型(木型)になっているものもあります。
ハイパーパラメーター
機械学習のアルゴリズムの動きをコントロールするパラメーターには「ハイパーパラメーター」と呼ばれるアルゴリズムの動きがあります。これは解析する人が決めるものです。
- 機械学習のモデルには、モデルの複雑さを調整する「ハイパーパラメーター」と呼ばれるパラメーターが存在している。
- ハイパーパラメーターとは機械学習のモデルが持つパラメーターの中で人が調整をしないといけないパラメーターのこと
「ハイパーパラメーター」を深く理解するためには数式を理解する必要がありますが、まずはこの2点を押さえておけばokです。
モデルの解釈可能性と予測性能(精度)
モデルの解釈の可能性というのは、「モデルの説明のしやすさ」を意味しています。
例えば、「野球選手の年俸と打率の関係」を表している線形回帰モデルであれば、「打率が高ければ高いほど、野球選手の年俸が高くなる」という解釈ができます。
一方で、予測性能(精度)は一般的には複雑であればあるほど予測精度が高くなる傾向にあります。
解釈は難しくなるのですが。。
機械学習のアルゴリズム(予測モデル)の種類について
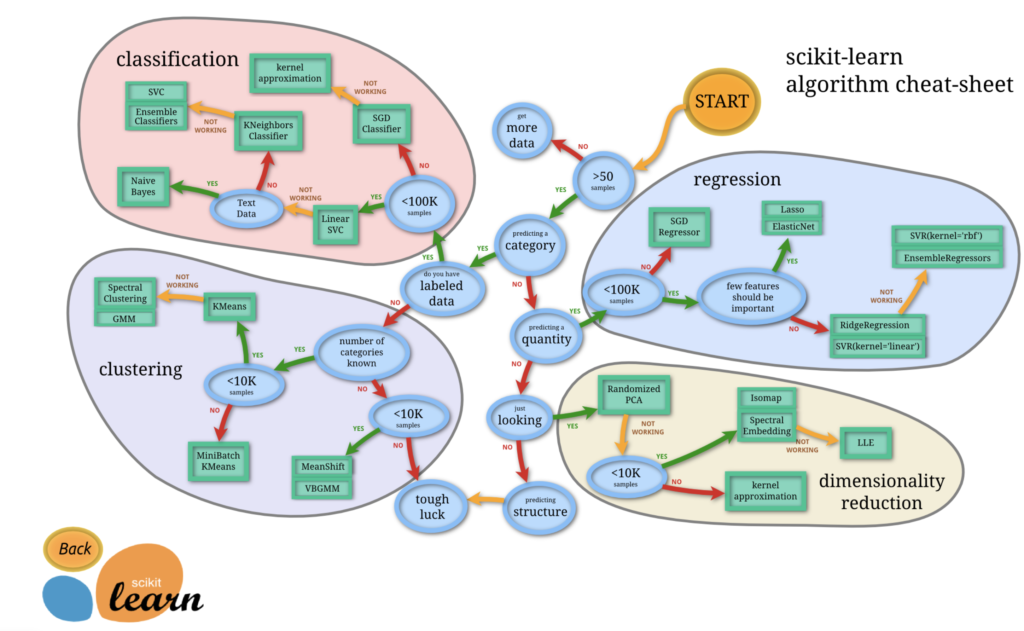
機械学習のライブラリであるscikit-learnを用いてどのアルゴリズムを使用するかは、scikit-learnの開発チームが作成したscikit-learn algorithm cheat-sheet が全体像となり、この表を参考に使用する具体的なアルゴリズムを決定します。
これらのアルゴリズムのうちのいくつかを、ここで紹介します。
線形回帰モデル
線形モデルを「野球選手の年俸と打率」の関係で説明します。具体的な線形モデルの使い方については次の記事をどうぞ。
簡単に解説すると、野球選手の打率で野球選手の年俸を予想するとします。
まずは「野球選手の打率(points)と年俸(salary)の関係」を散布図として表し、この関係性を表す1本の直線を引きたいのですが、どの様に直線を引けば良いのでしょうか。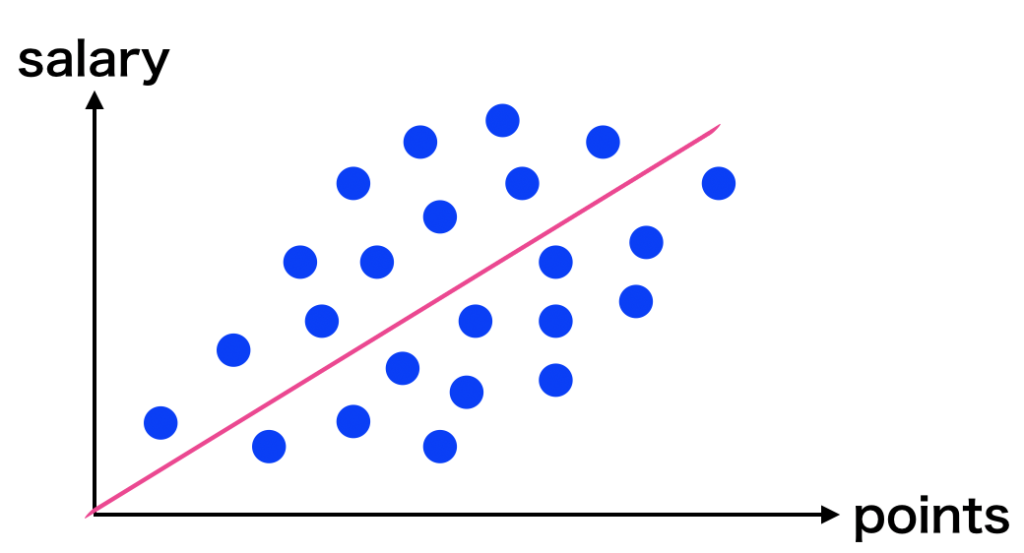
この直線モデルは線形回帰モデルといいますが、どの様に直線を引けば良いでしょうか。
線形回帰モデルは、実際の値と予測値の差の2乗を最小にする様に直線の傾きや切片を調整することでモデルを作っていきます。
線形回帰モデルのターゲット変数(野球選手の年俸：salary)は連続値です。
また、関数の形は直線です(多次元であれば、超平面になります)。目的関数は、「実際の値と予測値(直線上の値)の差の2乗を最小化する様に傾きや切片を調整する」関数です。
モデルの解釈可能性と予測性能(精度)はこの式「 \(S=a \times P+b\) 」を見ての通りで、特徴量である $P$ と係数 $a$ , $b$ の足し算掛け算で予測値 $S$ が算出できるので、解釈可能性は高い＝解釈はしやすい ですね。しかし、この直線モデルは直線のみで表現されているために予測性能は高いとは言えません。
線形回帰モデルの要点
- 予測したい対象の変数(ターゲット変数)：連続値
- 目的関数：差の2乗を最小化する様な傾きや切片を調整する関数
- 関数の形状：直線(多次元なら超平面)
- ハイパーパラメーター：なし
- モデルの解釈可能性と予測性能(精度)：解釈可能性は高い一方で、予測性能は高くない。
回帰木(決定木)
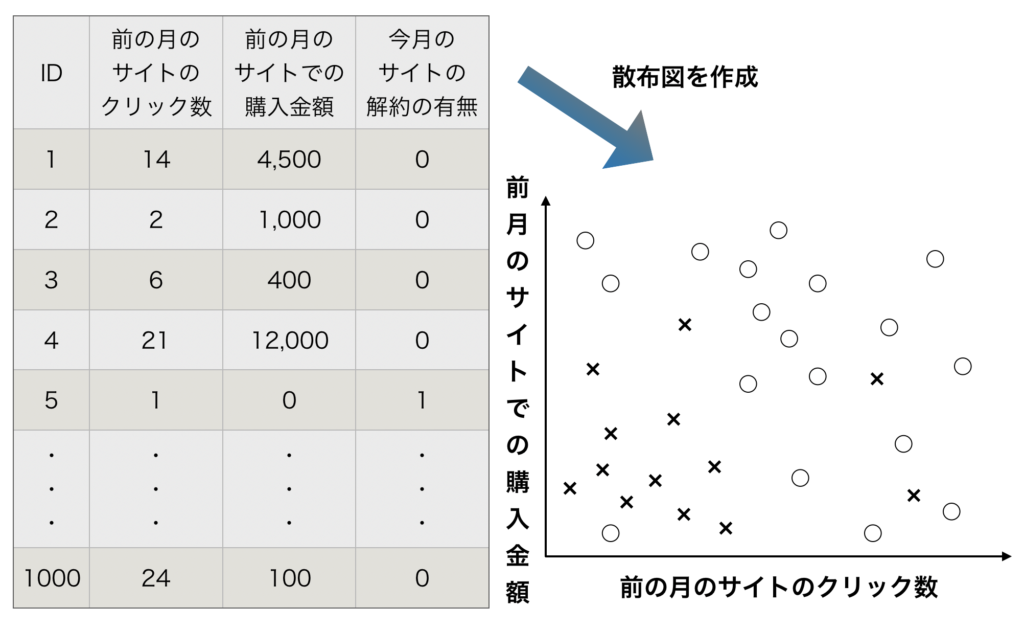
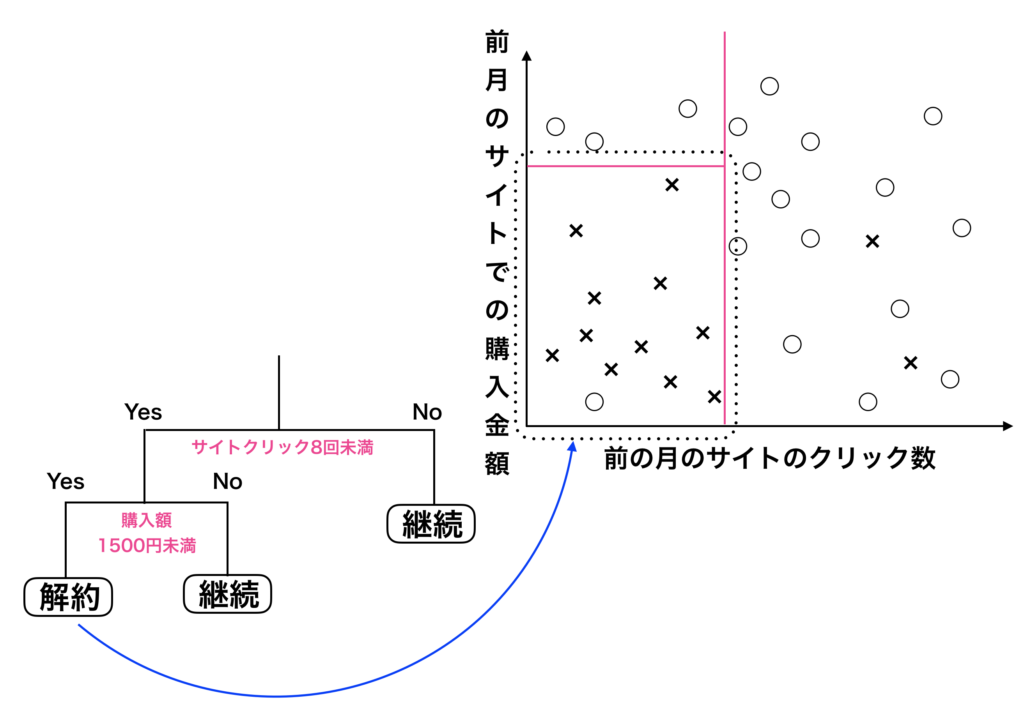
決定木モデルを「前月のサイトのクリック数と前月のサイトでの購入金額から今月(当月)の解約率」を予測するというモデルで解説します。
具体的な決定木モデルの使い方を知りたい方は次の記事をどうぞ。
-
【機械学習】回帰木・決定木で予測モデルを作成する【手順あり】
続きを見る
データから散布図を描き、回帰木(決定木)のモデルとなる分類図、およびツリーの図を作成するまでの流れが上図になります。
ランダムフォレスト
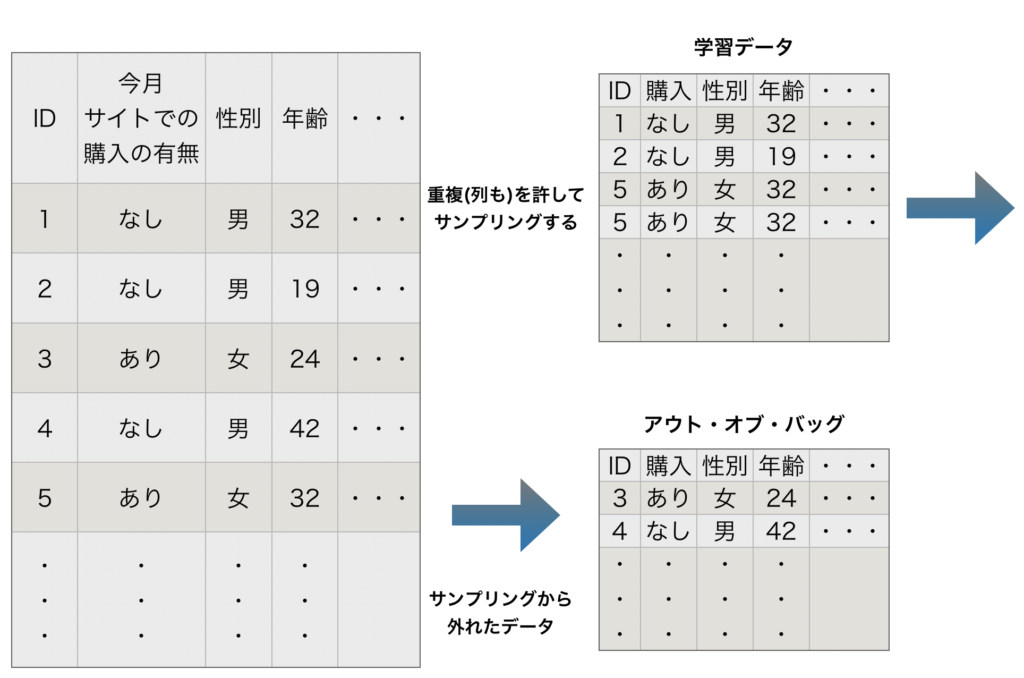
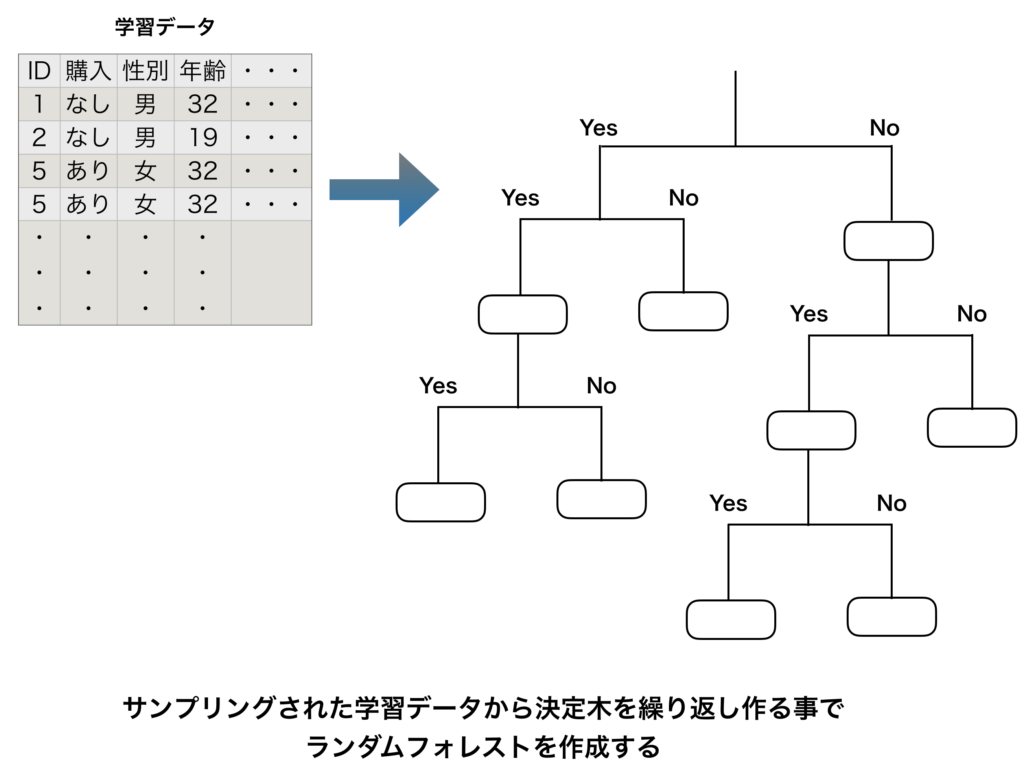
ランダムフォレストは、多種多様な決定木・回帰木を作り、各々の木(ツリー)
のアウトプットの多数決を取るアルゴリズムです。
ランダムフォレストについての特徴から具体的な実装方法まで詳しく知りたい方は次の記事をどうぞ。
-
【機械学習】ランダムフォレストとは【特徴の解説から実装まで】
続きを見る
格納されているデータから重複を許してサンプリングを行い、多種多様な決定木(ツリー)を作成するまでの流れが上図になります。
良い精度の機械学習アルゴリズム(予測モデル)を得るために行うべきこと4点
予測精度を高めるために必要なポイントを4つにまとめます。
予測精度を高めるためのポイント4つ
- アルゴリズムの選択
- 特徴量の選択
- ハイパーパラメーターのチューニング【グリッドサーチ】
- ホールドアウト法
- クロスバリデーション(交差検証)
では一つ一つ具体的に見ていきましょう。
機械学習アルゴリズム(予測モデル)の選択
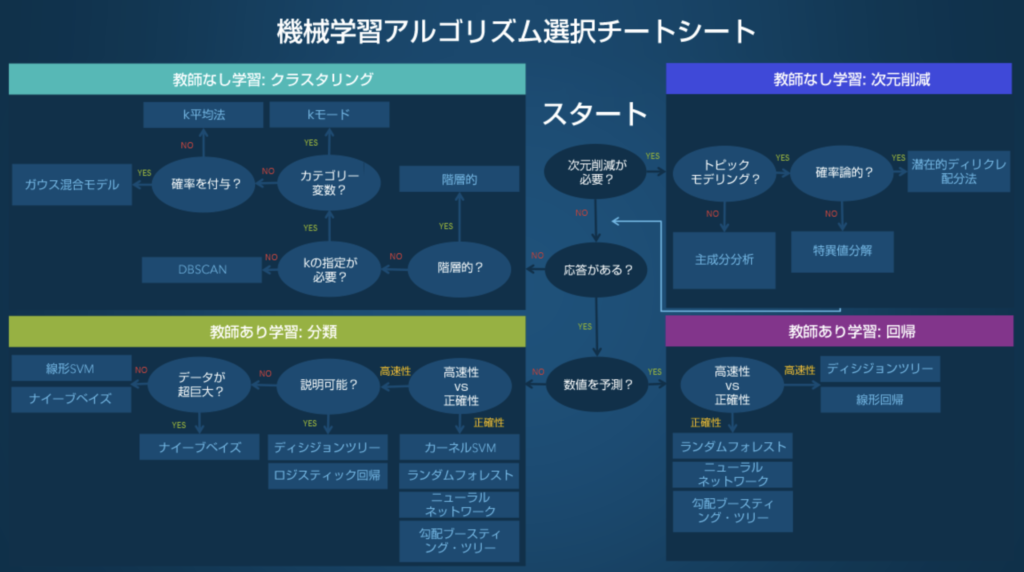
アルゴリズムの選択については、SAS Institute Japan が編集した "機械学習アルゴリズム選択ガイド" が参考になります。
» SAS Institute が作成した原本の記事はこちらです（英語版）
機械学習アルゴリズムを選択する際には、以下の様な要因に左右されます。
"機械学習アルゴリズム選択ガイド" より引用
- データの規模、品質、性質
- 利用できる計算時間
- タスクの緊急性
- データの利用目的（そのデータを利用して何がしたいのか？）
どのアルゴリズムが与えられたデータや求められるアウトカムに対して最も優れたパフォーマンスを示すかは、上記の要因を含めて検討する必要があります。同サイトに示されている 機械学習アルゴリズム選択チートシート を参考画像として掲載しておきます。
この様に、分析結果を何に利用されるのかを意識してアルゴリズムの特性や弱みや強みを理解してアルゴリズムを選択する事が重要です。
特徴量の選択
特徴量選択(フィーチャーセレクション：Feature Selection)をすることにより、予測性能(精度)が変わってきます。
特徴量選択を行うことにより得られるメリットには、以下の事があります。
- 良い特徴量選択は以下の恩恵が期待できる。
- 学習時間を減らせる
- モデルの解釈性が向上する
- モデルの精度が向上する
- 過学習を減らせる
しかし、特徴量選択は各々の特徴量を投入するかしないかで膨大な組み合わせができてしまいます。
そのためテキトーに特徴量選択を行うのではなく、以下のアプローチで特徴量選択を行います。
特徴量選択の種類
- 変数増加法
- 変数減少法
- 変数増減法
ハイパーパラメーターのチューニング
機械学習のアルゴリズムで良い精度のモデルを作るためには、ハイパーパラメータをチューニングする必要があります。その理由としては過学習を解決する必要があるためです。
機械学習のアルゴリズムの一つとして決定木がありますが、決定木の枝を増やして深くすればするほど、学習モデルの柔軟性は上がり、学習データにおけるエラーは下がっていきます。
極論ですが、決定木の深さを無限に深くすればするほど、完全にデータを分類し精度を爆上げする事ができます。
しかし、その一方で柔軟性を上げすぎると、テストデータの様な未知のデータ匂いてはエラー率が上がり過学習の状況に陥る可能性があります。
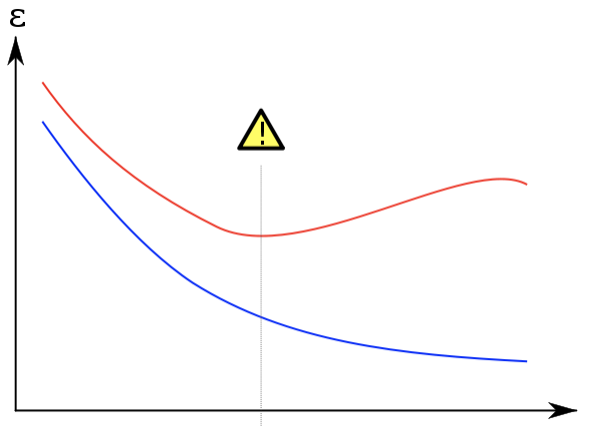
ハイパーパラメータのチューニングを行う目的としては、「テストデータ(未知のデータ)のエラーを下げる事」にあります。以下の図が過学習のモデルとなります。
この図では縦軸が「エラー」、横軸が「モデルの柔軟性」、青線が「学習データにおけるエラー」、「赤線が検証用データにおけるエラー」です。
では実際に、ハイパーパラメーターをチューニングする方法を紹介します。一般的な方法であれば「グリッドサーチ」という方法があります。
これはハイパーパラメータの組み合わせをあらかじめ用意しておいて、一つ一つ精度を確認するという方法になります。
グリッドサーチとランダムサーチ
ハイパーパラメーターのチューニング方法としては「グリッドサーチ」という方法が有名です。
グリッドサーチは「ハイパーパラメータの候補をひたすら挙げて、その組み合わせ全てでモデルを動かし、一番よかったものを選択する」という非常に単純なものです。
このグリッドサーチはハイパーパラメーターのチューニングの中でも一番簡単ですが、効率の良い方法とは言えません。ニ
ューラルネットワークのようなハイパーパラメータの数が多いモデルでグリッドサーチを行うと永遠に終わらなくなってしまう可能性があります。
より効率的な方法として「ランダムサーチ」があります。
こちらは上記テキストの11-4-4に記載があります。これは、ハイパーパラメータの候補を分布として与え、その分布からランダムに値を選択してモデルを動かします。
その結果をみて「効いているハイパーパラメータ」について掘り下げていき、効いていないものについては探索をやめます。
※ このDeep learningのテキストのChapter 11-4にハイパーパラメータのチューニングについて解説があります。グリッドサーチについては11-4-3で説明がされております。
※ ランダムサーチはこちらのscikit learnのサイトを参照にしましょう。
ホールドアウト法
機械学習・AIの分野ではモデルを評価する際に、あらかじめデータを無作為に訓練データとテストデータとに分けておきます。
方法としては、大きく分けてホールドアウト法と交差検証(クロスバリデーション)の2種類があります。
(交差検証の中にはk分割交差検証やシャッフル式k分割交差検証などの方法があり、その他にもジャックナイフ法などがありますが、この記事では省略します。これらの交差検証については以下のサイトを参考にしてください。)
» 機械学習モデルの検証の手法の種類とその注意点
ホールドアウト法は、様々な検証法の中でも最も簡易的な方法です。
まずデータを2分割します。訓練データを用いてモデルのパラメータを推定し、その後テストデータを使用して予測精度をチェックすることで、モデルの性能を評価します。
訓練データを更に 学習データ と 検証データ に分割し、学習データでモデルのパラメータを推定→検証データで学習結果を評価→テストデータでモデルの性能を最終評価する、という流れで行う場合もあります。
ホールドアウト法を利用する際のデメリットは、テストデータの取り方によって有利なモデルと不利なモデルが出てきうるということです。
これを回避するために、訓練データとテストデータへの分割を（無作為に）複数回行ない、予測性能の平均値を比較します。
以下参考に次に紹介する交差検証とホールドアウト法の違いを表でまとめておきます。
| 種類 | 概要 |
| ホールドアウト法 | 機械学習におけるデータのテスト方法の１つ。 教師データ（訓練データ）を「学習用」「評価用」に6対4などに割合で2分割して、学習済みモデルの精度を測定する方法。 |
| 交差検証法 | 教師データ（訓練データ）を3分割以上して、学習済みモデルの精度を測定します。 |
»【引用】ホールドアウト法と交差検証の違い【アルゴリズム雑記】
交差検証（クロスバリデーション）
上で出てきた「複数回のホールドアウト法」をより系統的に行うのが「交差検証（クロスバリデーション）」と呼ばれる方法です。
交差検証(クロスバリデーション)は一般的には「$K$ -分割交差検証（K-fold cross validation）」を指しますが、「シャッフル式k分割交差検証」を指す場合もあります。
ここではK-分割交差検証の流れについて解説していきます。
- データセット\(\mathcal{D}\)を、ほぼ同じ大きさのK個のサブセット\(\mathcal{D}_{1}, \mathcal{D}_{2}, \ldots, \mathcal{D}_{K}\) に分割する。
- サブセット\(\mathcal{D}_{1}\)をテストデータとして、その他のサブセット \(\mathcal{D}_{2}, \cdots, \mathcal{D}_{K}\) を用いてモデルを訓練し、予測精度を測る。
- 以降\(\mathcal{D}_{i}\)をテストデータ、その他を訓練データとする。これを順次繰り返して、全部で $K$ 個の性能を評価する。
このように、K-分割交差検証（K-fold cross validation）では単に無作為抽出を何度も行うのではなく、予めデータセットを分割してから検証を行います。
そうする事で、データの偏を最小限にして予測性能を評価できます。
では、具体的な数値でみていきましょう。まず、テストデータだけを分けておきます。
その残りのデータを、$k$ 個に分割しそれをkパターン作成します。仮に $k=5$ とした場合は、下図のような流れになります。
上図のうち黒丸が学習データで白丸が検証用のデータです。
5パターン全てでモデルの精査を行い、その中の平均や中央値などを評価してモデルを選びます。
最終的にそのモデルにたいして、テストデータで精度をテストします。
交差検証(クロスバリデーション)を行う際のデータ検証の流れを再度、以下に図示します。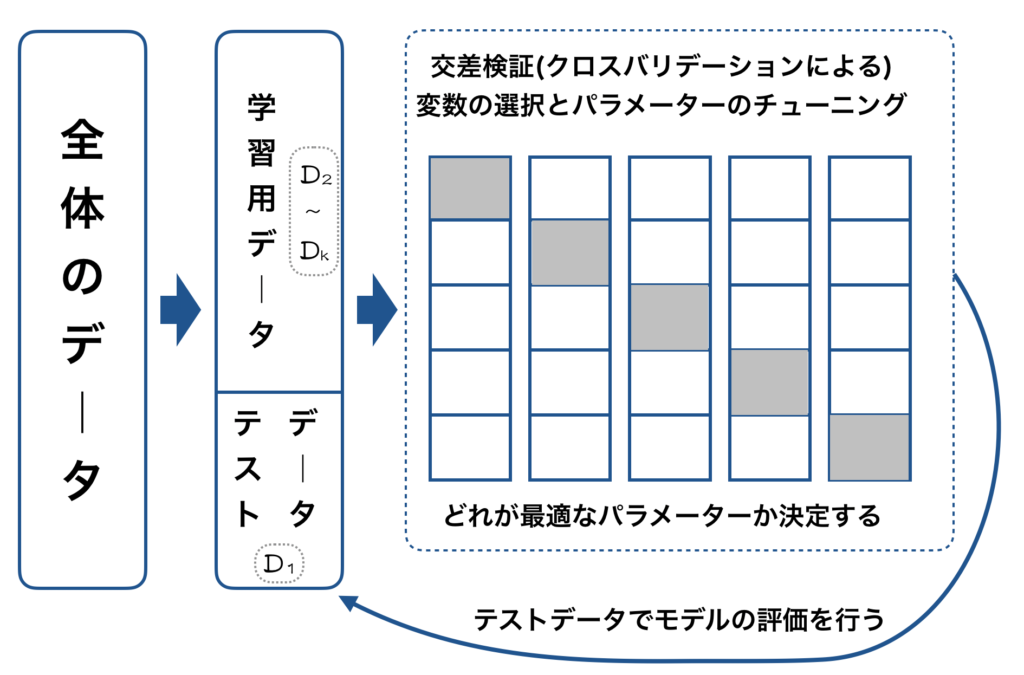
交差検証(クロスバリデーション)で変数の選択とはいパラメーターを決定したら、最終的にテストデータを使用してモデルの評価を行います。
モデルの評価を行い、それが十分な水準を満たしていれば分析プロセスの任務は完了するわけです。
まとめ|scikit-learnを使用して予測モデルを作成する方法
如何でしたでしょうか。
この記事では、scikit-learnを使用して予測モデルを作成する方法について解説させて頂きました。
機械学習のアルゴリズム（予測モデル）の作成が出来れば、次に行うのは評価の方法です。こちらについても改めて学習していきましょう。
長い記事でしたが、最後までお疲れ様でした。今回はこれで終わりとします。