【機械学習】線形回帰モデルで予測モデルを作成する【手順あり】

こんにちわ。

これまで以下の記事で、まずcsvからデータ得てデータの準備を行い、データの前処理を行なって散布図を描き、その散布図に適した予測モデル(線形モデル)を作成しました。(以下の順番の流れで記事を読んでいただくと理解が深まるかと思います)
[kanren id="13819"][kanren id="13901"][kanren id="13974"][kanren id="14250"]
この記事では、準備を行い、前処理をおこなったデータを用いて予測モデルの作成を行います。

一概に予測モデルと言っても、「線形モデル」「対数線形モデル」や「非線形モデル」、「多変数の線形モデル」など色々なモデルが存在します。

この記事ではこれらのモデルの中で、どのモデルが予測モデルとして最も優れているか検討していきます。

上記で紹介した3つの記事で作成した線形モデルは「推定年俸が打点に対して1次関数の直線で表される」という仮定を作成した以下のような予測モデルです。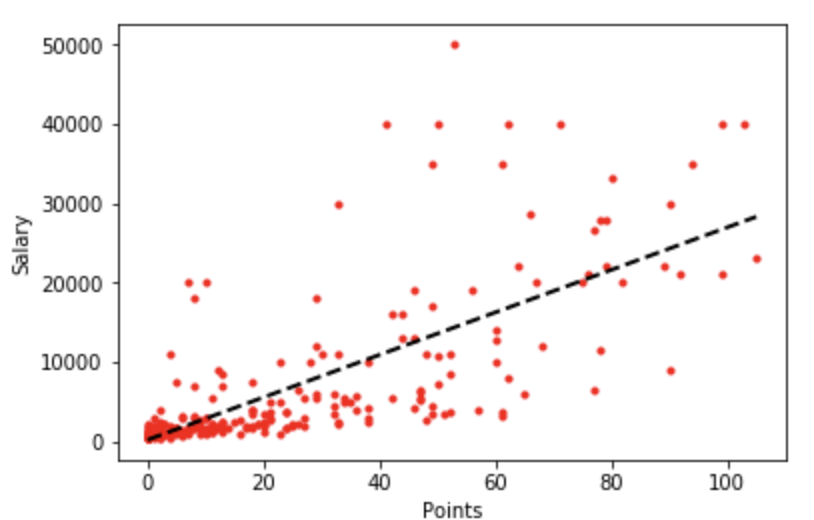

機械学習　予測モデル　評価
しかし、このように推定年俸が打点に対して単純に直線的な相関関係にあるわけはなく、「推定年俸を正確に予測する」という観点からは単純に直線モデルとして表すことは良くありません。

この記事では、別のモデルを試してなるべく散布図に合った相関関係のあるモデルを作成していきましょう。

予測モデルを評価する際に有用な「変数モデルの応用」について

① 予測モデルを評価する際の下準備を行う。

まず、必要なライブラリとデータを読み込み下準備を行いましょう。
（ numpy、pandas、matplotlibだけでなく、sklearn.linear_model.LinearRegressionも読み込んでおきます）

import math
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.optimize import least_squares
from sklearn.linear_model import LinearRegression

dataset = pd.read_csv("baseball_salary.csv")


# datasetから打点と推定年俸の配列をnumpy arrayとして取り出す

points = np.array(dataset["打点"])
salary = np.array(dataset["推定年俸"])

import math

import numpy as np

import matplotlib.pyplot as plt

import pandas as pd

from scipy.optimize import least_squares

from sklearn.linear_model import LinearRegression

dataset = pd.read_csv("baseball_salary.csv")

# datasetから打点と推定年俸の配列をnumpy arrayとして取り出す

points = np.array(dataset["打点"])

salary = np.array(dataset["推定年俸"])

※ from sklearn.linear_model import LinearRegressionこれが意味するのは、機械学習のうちのライブラリsklearnです。LinearRegressionは線形回帰を意味します。

fig = plt.figure()

# 年俸のみ対数に変換する
plt.plot(points, np.log10(salary), 'r.')
plt.xlabel("Points")
plt.ylabel("Salary")

# 対数に合わせた目盛りにする
plt.yticks((3, 4, 5), (1000, 1000, 10000))
plt.show()

fig = plt.figure()

# 年俸のみ対数に変換する

plt.plot(points, np.log10(salary), 'r.')

plt.xlabel("Points")

plt.ylabel("Salary")

# 対数に合わせた目盛りにする

plt.yticks((3, 4, 5), (1000, 1000, 10000))

plt.show()

描画すると以下の様になります。
[yoko2 responsive][cell]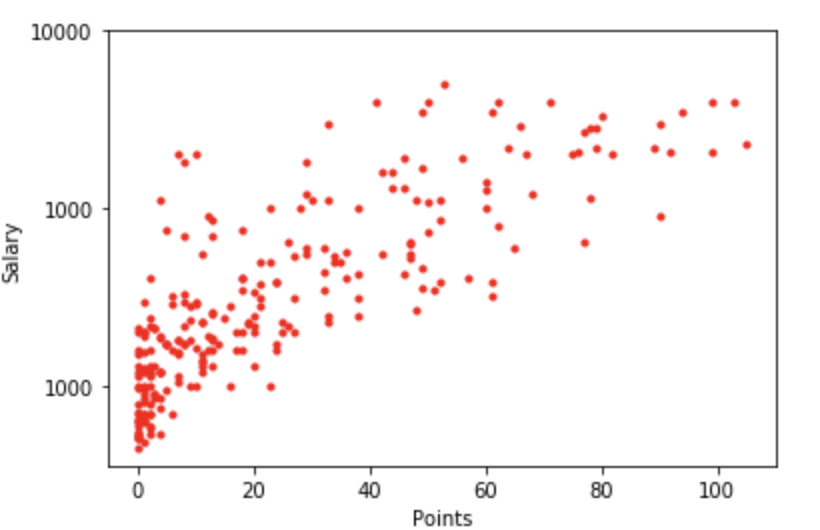
機械学習　予測モデル　評価 [/cell][cell]
[/cell][/yoko2]
上記のグラフは「推定年俸は打点から予測できる」という仮定から作成された直線の式になります。

あくまで「推定年俸は打点から予測できる」という仮定を残しつつ、どこまで精確な予測モデルを作れるかを考えてみましょう。

② 出力変数を対数に変換する

大きな数値、とくに年収や価格などは、金額があまりにも大きすぎることがあり、対数で表したほうが良い場合があります。

このように大きい値を扱う際には、対数に変換した方が様々なモデルに合うことがあり、非常に有用な場合が多いです。
» 【Wikipedia】ヴェーバーの法則

それでは、以下のコードで下の手順に従って、出力変数を対数で表すようにしましょう。[box class="box6"]

縦軸を salaryではなく、10を底とする対数に変換してプロットします。具体的にはnp.log10(salary)とします。
対数をとったままnp.log10(salary)とすると、$y$ 軸の目盛りが対数の値が表示されてしまいます。そのためplt.yticks()を用いて元々の値を表示させる様にしましょう。
np.log10(salary), plt.yticks() の2つの使い方を覚えておきましょう [/box]

※ 単純に $y$ 軸を対数表示にするだけなら、plt.plot(points, salary, '.')と合わせてplt.yscale("log")を用いることで実現できます。

ただ今回の場合は、この対数年俸データをあとで線形モデルに加えて描画すること、そしてあとで打点を対数表示する際により便利なことから、こちらの方法を用いました。

fig = plt.figure()

# 年俸のみ対数に変換する
plt.plot(points, np.log10(salary), 'r.')
plt.xlabel("Points")
plt.ylabel("Salary")

# 対数に合わせた目盛りにする
plt.yticks((3, 4, 5), (1000, 1000, 10000))
plt.show()

fig = plt.figure()

# 年俸のみ対数に変換する

plt.plot(points, np.log10(salary), 'r.')

plt.xlabel("Points")

plt.ylabel("Salary")

# 対数に合わせた目盛りにする

plt.yticks((3, 4, 5), (1000, 1000, 10000))

plt.show()

機械学習　予測モデル　評価 [box class="box2"]※ plt.plot() の引数の使い方を忘れてしまった方は以下のサイトを参照ください。
» Matplotlib.pyplotのplotの全引数を解説

※ さらに plt.ystick やplt.xstick の引数については以下の記事が参考になりますので、参照してみてください。
» matplotlib グラフの作成 [/box]
対数を使用をすると、より直線的な描図出来る(様な気がします)。
ですので、値が大きい場合には、対数を用いるのは良いのではと思います。

今回予想するモデルは線形モデルですが、重要な点として「打点から年俸の対数を予測する」ということがあります。従って、今まで使用してきた式は以下の様になりますが、変形する必要があります。

$\log _{10} S=a \times P+b$

実際に、年俸を対数変換したものに変形してみましょう。

$S=10^{a \times P+b}$

このように元データを直接入力や出力データとするのではなく、今回の様に対数変換するなど、何らかの変換を施す方法は、AI・機械学習の業界で一般的に行われています。

そしてこの手法のことを特徴量エンジニアリング(feature engineering)と言います（「特徴量 feature」は、入力/出力データを指しています）。

特徴量エンジニアリングは、良いモデルを探すためにはほぼマストなプロセスです。

KaggleなどのAIコンテストでも、元々のデータ（特徴量）をそのまま使うモデルはほとんどないのではないでしょうか。

対数への変換することは、代表的な特徴量エンジニアリングの方法ですので覚えておきましょう。

では早速、モデル作りを始めてみましょう。

③ 実際に出力変数を対数に変換し、モデルを作成する

では実際に以下の手順に従って、モデルを作成して行きましょう。[box class="box6"]

salaryに対する10を底とする対数logsalaryを作りましょう。
入力数pointsに対してlogsalaryを予測する線形モデルloglinearを作ります。さらに、係数と切片を浮動小数点数として出力します（係数や切片などのモデルの出力は配列形式になっていることに注意）。
pointsとlogsalaryを散布図に重ねて、loglinearの直線を加えます。
加えて、pointsとsalaryも散布図に重ねて、loglinearの曲線を描きます。[/box]では、この手順に従って、コードを書いていきましょう。

STEP1：縦軸 $y$ 軸に対数を取る。

salaryに対する10を底とする対数logsalaryを作ってください。

logsalary = np.log10(salary)

1	logsalary = np.log10(salary)

※ NumPyは numpy.log10() で10が底の対数関数ができますので、覚えておきましょう。» アルゴリズム雑記

STEP2：points に収納されているデータの数を確認する。

in[]

points.shape

1	points.shape

out[]

(241,)

(241,)

STEP3：予測する線形モデルを作成し、係数と切片を算出する。

入力pointsに対してlogsalaryを予測する線形モデルloglinearを作り、係数と切片を取り出してください。

loglinear = LinearRegression().fit(points.reshape((-1,1)), logsalary.reshape((-1, 1)))
a = loglinear.coef_[0,0]
b = loglinear.intercept_[0]

loglinear = LinearRegression().fit(points.reshape((-1,1)), logsalary.reshape((-1, 1)))

a = loglinear.coef_[0,0]

b = loglinear.intercept_[0]

[box class="box29" title="1行目のコードの解説"]ここで、1行目のコードについて解説します。

②で確認した様にpointsには241個のデータが入っていますね。

このデータを、reshape(-1,1)で $241×1$ の配列に変換しています。今までは(241, )という「ただの241個の数字の並び」だったのですが、reshape(-1,1)を使用することで $241×1$ の配列に変換されるわけです。

モジュールによってはこのように配列の形式を $a×b$ といった形に指定してくるものがあります。

また、.fit は分類器にかけるというイメージです。[/box]
[box class="box29" title="a, bに関するコードについての解説"]「loglinear.coef」と「loglinear.intercept」についての解説です。

これは作成したモデルのパラメータを確認するコードです。loglinear.coef は回帰係数、loglinear.intercept は切片を返します。

例えば $y=ax+b$ というモデルであれば、loglinear.coef で $a$ の値、loglinear.intercept で $b$ の値を確認することができます。

coef_ はcoefficientの略ですので「傾き」、intercept_ は「切片」を意味しています。loglinear.coef_ として出力すると、array が二重になっているので数値だけを取り出すために[0,0]としています。[/box]

STEP4：予測した線形モデルを描出する。

上で作ったようなpointsとlogsalaryの散布図に重ねて、予測したloglinearの直線を描いてください。
こんどはpointsとsalary（もとの値）の散布図に重ねて、予測したloglinearの曲線を描いてください。

# figure内の枠の大きさとどこに配置している。subplot(行の数,列の数,何番目に配置しているか)
fig, axes = plt.subplots(1,2,sharex=True) 

# グラフのFontや文字サイズなど細かい調整
fig.set_size_inches(12, 4)

#  np.linspace(a, b, c) はa〜bまでcの間隔でスライスする
pvalues = np.linspace(points.min(), points.max(), 100)
def _calc(p):
    return a*p + b

# logsalary vs loglinear
# matplotlib - 目盛、グリッドの調整方法 
axes[0].plot(points, logsalary, 'g.')
axes[0].plot(pvalues, _calc(pvalues), 'm--', lw=2)
axes[0].set_yticks((3,4,5))
axes[0].set_yticklabels((1000, 10000, 100000))

# salary vs loglinear
axes[1].plot(points, salary, 'r.')
axes[1].plot(pvalues, np.power(10, _calc(pvalues)), 'm--', lw=2)

for ax in axes:
    ax.set_xlabel("points")
    ax.set_ylabel("salary")
fig.savefig("images/loglinear_output.png")
plt.show()

# figure内の枠の大きさとどこに配置している。subplot(行の数,列の数,何番目に配置しているか)

fig, axes = plt.subplots(1,2,sharex=True)

# グラフのFontや文字サイズなど細かい調整

fig.set_size_inches(12, 4)

# np.linspace(a, b, c) はa〜bまでcの間隔でスライスする

pvalues = np.linspace(points.min(), points.max(), 100)

def _calc(p):

return a*p + b

# logsalary vs loglinear

# matplotlib - 目盛、グリッドの調整方法

axes[0].plot(points, logsalary, 'g.')

axes[0].plot(pvalues, _calc(pvalues), 'm--', lw=2)

axes[0].set_yticks((3,4,5))

axes[0].set_yticklabels((1000, 10000, 100000))

# salary vs loglinear

axes[1].plot(points, salary, 'r.')

axes[1].plot(pvalues, np.power(10, _calc(pvalues)), 'm--', lw=2)

for ax in axes:

ax.set_xlabel("points")

ax.set_ylabel("salary")

fig.savefig("images/loglinear_output.png")

plt.show()

すると以下の様に描図されます。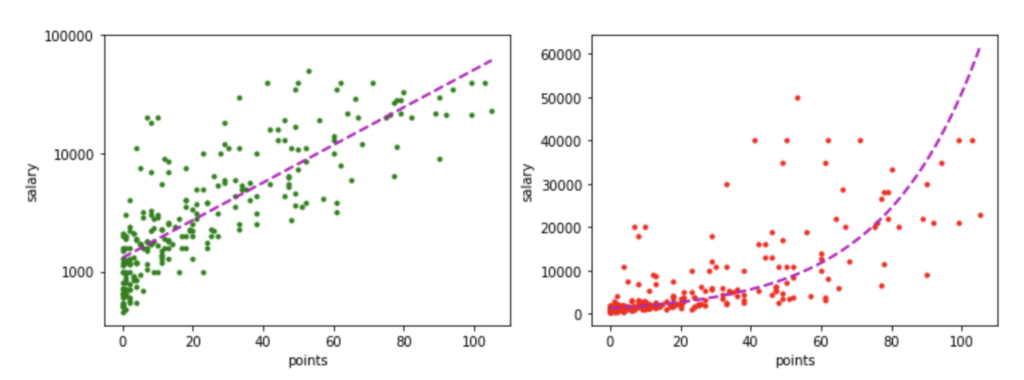機械学習　予測モデル　評価

ここでコードの解説です。[box class="box3"]

plt.subplots(1,2,sharex=True)　は figure の表示の仕方についてのコードになります。
plt.subplot(行の数,列の数,何番目に配置しているか) を意味しています。
» matplotlib基礎 | figureやaxesでのグラフのレイアウト
fig.set_size_inches(12, 4) はグラフのFontや文字サイズなど細かい調整をするメソッドになります。.set_size_inches(12, 4) は「横 12 inch, 縦 4 inchに指定する」という事を意味します。
» 【Takuya Aoyama's Work】Matplotlibを用いたグラフの描画
pvalues = np.linspace(points.min(), points.max(), 100) は「points.min()〜 points.max()」を100当分にスライスする」という子yとを意味します。「np.linspace(a, b, c) は $a〜b$ まで $c$ の間隔でスライスする」という事を意味します。
axes[0]についての解説です。subplot(1, 2) で1行2列の作図スペースを作成しました。図を書くには「この作図スペースのどこに書くか」を指定する必要があります。axes[0] は、最初のスペースに書くという指定です。
ちなみに、axex[1] で右側に作図できます。
yticksとytickslabelsの違いは「メモリを設定する」のと「メモリに対応するラベルを設定する」という違いがあります。
axes[0].plot(points, logsalary, 'g.') は「左の図表の $x$ 軸にpoints, $y$ 軸にlogsalary、ドットを緑色にする」という意味のコードになります。
axes[0].plot(pvalues, _calc(pvalues), 'm--', lw=2) は「lw=2 で線の太さ、‘ m-- ’はcolor = マゼンタ、線の種類は点線という意味」になります。文字で指定することもできますが、このように省略して書くこともできます。[/box]ここで目盛りについての解説です。[box class="box6"]
fig, axes = plt.subplots(1,1,sharex=True)<br>plt.plot(points, logsalary, 'k.')
1
fig, axes = plt.subplots(1,1,sharex=True)<br>plt.plot(points, logsalary, 'k.')
ここまでのコードでは、縦軸の目盛りが0.5刻みで振られています。
これは自動的にmatplotlibのほうで目盛りを決めてくれます。この目盛りでは都合が悪い場合、こちらで目盛りを指定することができます。先ほどのコードに下記のコードを加えます。
axes.set_yticks((3,4,5))
1
axes.set_yticks((3,4,5))
縦軸で3,4,5に目盛りが入ったかと思います。最後に、これまでのコードに下記のコードを加えます。
axes.set_yticklabels((1000, 10000, 100000))
1
axes.set_yticklabels((1000, 10000, 100000))
これで、先ほど3,4,5と目盛りを入れた箇所が1000, 10000, 100000で上書きされます。
fig.savefig("images/loglinear_output.png") は「images」というフォルダに「loglinear_output.png」という形で画像保存し出力する、という意味です。imagesフォルダではなく作業している場所にそのまま図を作成したい場合には、images/を無くして下記のように書きますと保存できます。
fig.savefig(“loglinear_output.png”)[/box]

目盛り、ラベルなどを設定するメソッドについて

【Qiita】seabornの細かい見た目調整を諦めないに非常に分かりやすい解説がありましたので、seaborn の目盛りやラベルを設定するメソッドを表形式でまとめておきます。

メソッド	説明
set_axis_labels([x_var, y_var])	左端と下端のラベルを設定
set_xlabels([label])	下端のラベルのみ設定
set_ylabels([label])	左端のラベルのみ設定
set_titles([template, row_template, …])	全ての`Axes`の上部またはグリッド上部や右側に列や行のカテゴリや値を示すタイトルを設定
set_xticklabels([labels, step])	下端の数字ラベルを設定
set_yticklabels([labels])	左端の数字ラベルを設定

» seaborn.FaceGrid
» 【Qiita】seabornの細かい見た目調整を諦めない

④ 非線形モデル

次に年俸だけではなく、打点も対数にして描図してみます。

しかしsalaryとは異なり、pointsを対数にしようとエラーがでます。これは打点0の場合に、対数が計算できないことに起因します。エラーはこの様な感じで出ます。

pointsを対数にしようとした時に表示されたエラー。打点が0の値の場合に、対数が計算できないことを意味する。
もとのデータであるpointsを使用して対数にするには、$\log _{10} P_{i}$ ではなく $\log _{10}\left(P_{i}+1\right)$ にします。こうすることで、打点0の場合でも計算する事ができます。しかも比率の関係をある程度保てたまま特徴量を変換する事が出来るわけです。

最初に logpoints と logsalary の関係をプロットしてみます。まずは打点0の場合に対数にする際に、エラーになるのを回避するための処置を行います。
以下のコードををjupyter notebookに入力してみてください。

In[]

logpoints = np.log10(points + 1)

1	logpoints = np.log10(points + 1)

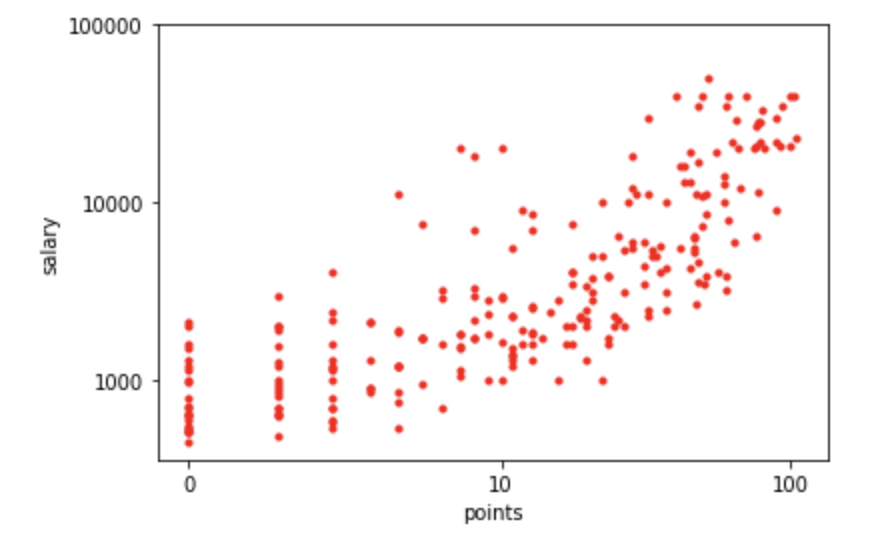
このlogpointsに加えて先ほどのlogsalaryを使い、2つの特徴量の関係をプロットしてみます：

plt.figure()
plt.plot(logpoints, logsalary, 'r.')
plt.xticks((0, math.log10(11), math.log10(101)), (0, 10, 100))
plt.yticks((3, 4, 5), (1000, 10000, 100000))
plt.xlabel("points")
plt.ylabel("salary")
plt.show()

plt.figure()

plt.plot(logpoints, logsalary, 'r.')

plt.xticks((0, math.log10(11), math.log10(101)), (0, 10, 100))

plt.yticks((3, 4, 5), (1000, 10000, 100000))

plt.xlabel("points")

plt.ylabel("salary")

plt.show()

機械学習　予測モデル　評価 ※ グラフの設定の方法については以下のサイトを参考にしましょう。
» matplotlibグラフの設定
[box class="box29" title="ticks と labelsについて"]plt.yticks((3, 4, 5), (1000, 10000, 100000)) についての解説です。matplotlibの公式サイトを確認しましょう。yticks(ticks=None, labels=None, **kwargs)とあり、パラメータはticksとlabelsであることがわかります。どちらのパラメータも入れず、ただyticks()とすれば現在のyの目盛りを取得することができますが、このパラメータを利用しますと「目盛りはticksの位置に打ってその目盛りのラベルはlabelsにする」という指定ができます。今回であれば、plt.xticks((0, math.log10(11), math.log10(101)), (0, 10, 100))でx軸の0, log10(11), log10(101)の位置に目盛りを打ってそのラベルは0, 10, 100にする、という意味になります。[/box]
$x$ 軸、$y$ 軸共に対数のグラフにしたことで、「ある打点までは年俸がほぼ変わらず(最低年俸制度と言うべきでしょうか)」「以降は指数的に年俸が増える」という関係が予想されます。

このグラフのポイントとしては、このような二相性の関係は、単純な線形モデルではモデル化できない事があります。そこでここでは、以下のように非線形モデルの数式を作り当てはめます。

$\log _{10} S=\left\{\begin{array}{ll}{b} & {(\text { constant })} &{(P>h)}\\ {a \times\left(\log _{10}(P+1)-\log _{10}(h+1)\right)+b} & {(P>h)}\end{array}\right.$

両対数グラフ上でのモデルの大まかな形は以下の通りで、左側の水平線の高さが $b $ 、折れ目の点が $P_{t h}$ になります（出典元: Wikipedia(en) の “Activation function” にある “Rectified linear unit” のグラフ）：

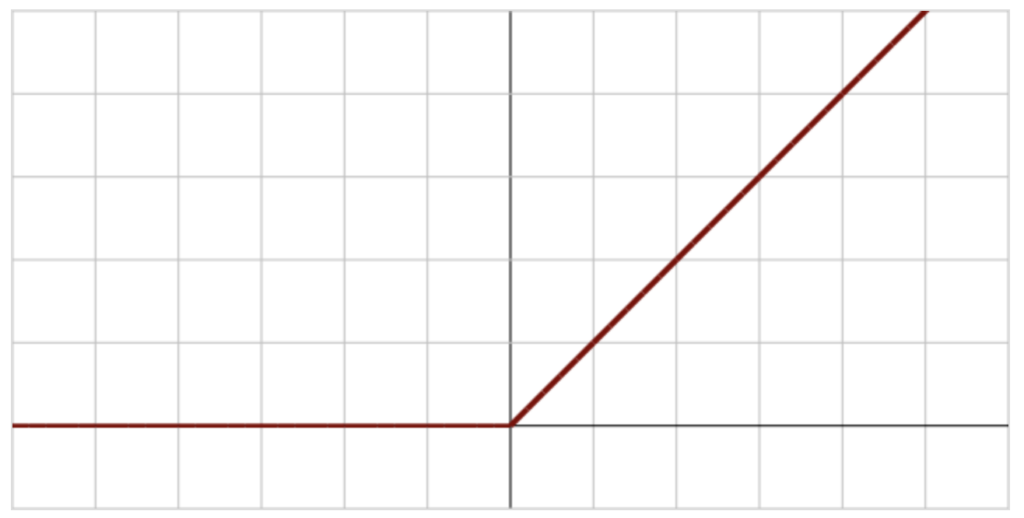
» Wikipediaの “Activation function” にある “Rectified linear unit” のグラフ

便宜上$H=\log _{10}(h+1)$とすると、この非線形モデルと残差を定義する関数は以下のように定義できます。

def nonlinear(x, logpoints=logpoints):
    a,b,H = x
    ret = np.empty(logpoints.size, dtype=float)
    above = logpoints > H
    below = ~above
    ret[below] = b
    ret[above] = a*(logpoints[above] - H) + b
    return ret

def residuals_nonlinear(x):
    return nonlinear(x) - logsalary

def nonlinear(x, logpoints=logpoints):

a,b,H = x

ret = np.empty(logpoints.size, dtype=float)

above = logpoints > H

below = ~above

ret[below] = b

ret[above] = a*(logpoints[above] - H) + b

return ret

def residuals_nonlinear(x):

return nonlinear(x) - logsalary

[box class="box3"]

(x, logpoints=logpoints):

1	(x, logpoints=logpoints):

のうちの、logpoimnts = logpoints について解説します。関数にlogpointsという引数を設定しているのですが、もしこの引数に何も値が与えられなければ今まで定義されているlogpointsを使う、という意味です。logpointsはlogpoints = np.log10(points+1)と最初に設定されています。

a,b,H = x は $x$ は要素が3つある変数のため、それら3つの要素に1つずつa, b, Hと名前をつける、という事を意味しています。

np.empty() の引数()であるlogpoints.size, dtype=float　のうちの左のlogpoints.sizeの意味についての解説です。logpoints.sizeで実行してみるとよく分かります。logpoints.size はlogpoints という変数の中に入っている要素の数を出力します。
よって、logpointsの要素の数と同じ長さの空の配列を作りたいということを np.empty() は意味しています。[/box]

⑤ 実際に非線形モデルを表示してみる

では早速、以下の手順に従って、実際に非線形モデルを表示してみましょう。
[box class="box6"]

residuals_nonlinearとscipy.optimize.least_squaresを用いて、この非線形モデルnonlinearのパラメータである $(a, b, H)$ を推定してみましょう。
logpointsとlogsalaryの散布図に重ねて、予測したnonlinearの直線を描図します。
こんどはpointsとsalary（もとの値）の散布図に重ねて、予測したnonlinearの曲線を描図します。[/box]

では早速この手順に従って、コーディングしていきましょう。

STEP1

residuals_nonlinearとscipy.optimize.least_squaresを用いて、この非線形モデルnonlinearのパラメータ $(a, b, H) $ を推定してみます。

opt = least_squares(residuals_nonlinear, (0,0,0))
if opt['success'] == False:
    raise RuntimeError("estimation failed")
theta = opt['x']

opt = least_squares(residuals_nonlinear, (0,0,0))

if opt['success'] == False:

raise RuntimeError("estimation failed")

theta = opt['x']

STEP2, STEP3

[box class="box6"]

上で作ったようなlogpointsとlogsalaryの散布図に重ねて、予測したnonlinearの直線を描いてください。
こんどはpointsとsalary（もとの値）の散布図に重ねて、予測したnonlinearの曲線を描いてください。[/box]

in[]

fig, axes = plt.subplots(1,2)
fig.set_size_inches(12, 4)

logpvalues = np.linspace(logpoints.min(), logpoints.max(), 100)
pvalues = np.linspace(points.min(), points.max(), 100)
estimate = nonlinear(theta, logpoints=logpvalues)

# logsalary vs nonlinear
axes[0].plot(logpoints, logsalary, 'k.')
axes[0].plot(logpvalues, estimate, 'm--', lw=2)
axes[0].set_yticks((3,4,5))
axes[0].set_yticklabels((1000, 10000, 100000))
axes[0].set_xticks((0, math.log10(11), math.log10(101)))
axes[0].set_xticklabels((0, 10, 100))

# salary vs nonlinear
axes[1].plot(points, salary, 'k.')
axes[1].plot(pvalues, np.power(10, nonlinear(theta, logpoints=np.log10(pvalues+1))), 'm--', lw=2)

for ax in axes:
    ax.set_xlabel("points")
    ax.set_ylabel("salary")
fig.savefig("images/nonlinear_output.png")
plt.show()

fig, axes = plt.subplots(1,2)

fig.set_size_inches(12, 4)

logpvalues = np.linspace(logpoints.min(), logpoints.max(), 100)

pvalues = np.linspace(points.min(), points.max(), 100)

estimate = nonlinear(theta, logpoints=logpvalues)

# logsalary vs nonlinear

axes[0].plot(logpoints, logsalary, 'k.')

axes[0].plot(logpvalues, estimate, 'm--', lw=2)

axes[0].set_yticks((3,4,5))

axes[0].set_yticklabels((1000, 10000, 100000))

axes[0].set_xticks((0, math.log10(11), math.log10(101)))

axes[0].set_xticklabels((0, 10, 100))

# salary vs nonlinear

axes[1].plot(points, salary, 'k.')

axes[1].plot(pvalues, np.power(10, nonlinear(theta, logpoints=np.log10(pvalues+1))), 'm--', lw=2)

for ax in axes:

ax.set_xlabel("points")

ax.set_ylabel("salary")

fig.savefig("images/nonlinear_output.png")

plt.show()

out[]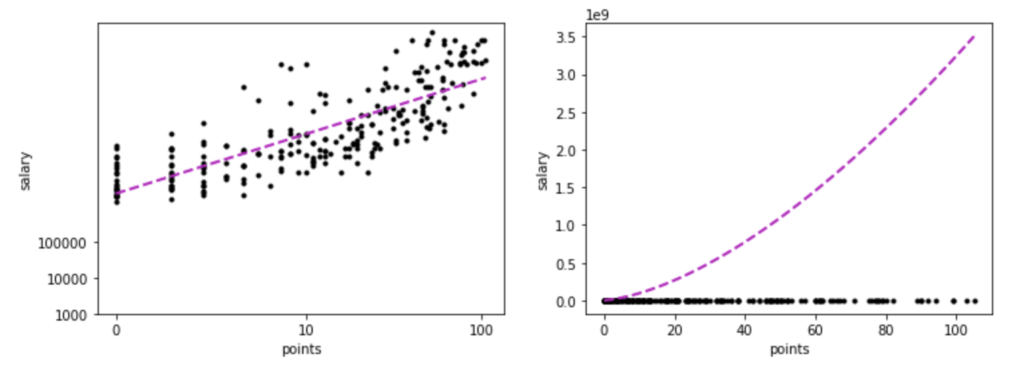
機械学習　予測モデル　評価
この様に出力されます。

※ np.power についてはNumpyの公式ページに分かりやすく解説されています。

まとめ

機械学習において予測モデルを作成する方法について解説しました。