ベイズ更新の概念を理解する【ベイズ更新を例題を用いて解説】

今回の記事はベイズの定理を応用した内容になります。

ベイズ統計の理論と方法の基本的内容については以下の記事を参照ください。

: ベイズ統計の理論と方法【初心者向け】
続きを見る

また、ベイズ統計の理論の流れと、実際の事後確率の計算方法については以下の記事を参照ください。

: ベイズ統計の理論と実際の計算方法【初心者向け】
続きを見る

　本記事の学習内容です。

ベイズ更新を利用して事後分布の計算ができる
例題を通して、実際にベイズ更新ができる

では早速、見ていきましょう。

ベイズの更新を例題を交えて解説

ベイズの定理の復習

まず、ベイズの定理をおさらいします。

$$f(\theta | \mathcal{D})=\frac{f(\mathcal{D} | \theta) f(\theta)}{f(\mathcal{D})}$$

式の各々のパーツの名称です。

$f(\theta | \mathcal{D})$：事後分布　(結果 ${D}$ が与えられた時の原因 $θ$ の条件付き確率 )

$f(\mathcal{D} | \theta)$：尤度関数　(カーネルと言います。原因( $D$ )と結果( $θ$ )を紐づけている部分)

$f(\theta)$：事前分布　(原因についての事前知識の確率分布)

$f(\mathcal{D})$：エビデンス　(事後分布の規格化定数)

上の式でもわかる様に、$f(\theta | \mathcal{D})$ (事後分布)は、$f(\mathcal{D} | \theta)$ (尤度関数)と$f(\theta)$ (事前分布)の積を$f(\mathcal{D})$ (エビデンス)で割って求める事が出来ます。

要するに事後分布とは、結果( $D$ )が与えられた時に、原因( $θ$ )を推定する確率のことです。

今回は、$f(\mathcal{D} | \theta)$：尤度関数　(カーネル) のデータが1個,2個,3個と増えていった際に、$f(\theta | \mathcal{D})$ 事後分布にどのような影響があるのかを考えていきます。

ベイズの更新(袋の問題で詳しく説明)

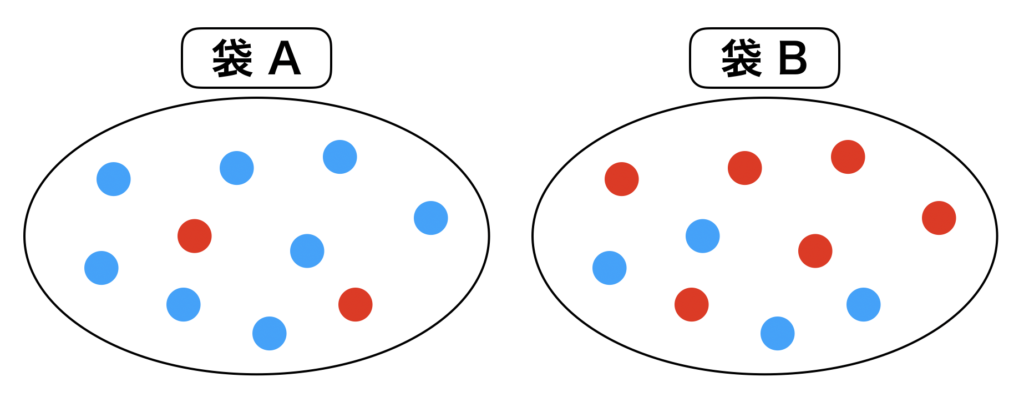
観測するデータが増えていくと、事後分布にどのような影響を与えるのか。

ベイズ更新の流れを、袋Aと袋Bの問題を例えにして進めていきましょう。

袋A 青; 8個　赤; 2個
袋B 青; 4個　赤; 6個

問題設定

袋を1/2の確率でランダムに選び、袋から復元抽出で 10回取り出す。

取り出した玉の結果は{ b, r, b, r, b, b, b, r ,b ,r }であった。

この結果から、選んだ袋はどちらと考える事ができるか。

この計算を実際に行なっていきましょう。

ベイズ統計を利用した実際の計算の流れ

では、実際に計算していきましょう。

$$p(x | y) \propto \prod_{i} p\left(y_{i} | x\right) p(x)$$

この式を ① とします。

この式がピントこない方はこの記事を復習してください。

: ベイズ統計の理論と方法【初心者向け】
続きを見る

データが1個の場合
①の式より

$$p\left(x | y_{1}\right) \propto p\left(y_{1} | x\right) p(x)$$

この式が成立します。

では、データが2個の場合にはどのようになるのでしょうか。

①の式より

$$p\left(x | y_{1}, y_{2}\right) \propto p\left(y_{2} | x\right) p\left(y_{1} | x\right) p(x)$$

が成立します。

ここで、ベイズの定理を利用すると

$$p\left(y_{2} | x\right) p\left(y_{1} | x\right) p(x) \propto p\left(y_{2} |x\right) p\left(x | y_{1}\right)$$

である事がわかります。

すなわち。

$$p\left(x | y_{1}, y_{2}\right) \propto p\left(y_{2} |x\right) p\left(x | y_{1}\right)$$

と式変形を行う事ができます。

$p\left(y_{2} |x\right) $ 　これは尤度関数(カーネル)のことでした。

また、

$p\left(x | y_{1}\right)$　これは事前分布の事でしたね。

これらの式を利用することで、事後分布である$p\left(x | y_{1}, y_{2}\right)$ を求める事が出来る訳です。

すなわち、$ y₁ $ や $ y₂ $ などのデータを用いて、逐一データを取りこむ事ができます。

この事を「ベイズ更新」と言います。

演習：袋Aと袋Bの問題を使用してデータの数で事後分布がどのように変化をするのかを実装してみましょう。

問題設定

袋を1/2の確率でランダムに選び、袋から復元抽出で 10回取り出す。
取り出した玉の結果は{ b, r, b, r, b, b, b, r ,b ,r }であった。

袋A 青; 8個　赤; 2個
袋B 青; 4個　赤; 6個

ここで、演習内容です。

演習問題

データの数に応じて、事後分布がどのように変化をするのかを見ていきましょう。

ここで、事後分布を扱う際に、Bernoulli(ベルヌーリ分布)を使用しますので、それについて詳しく解説していきます。

ベルヌーイ分布を利用してベイズ更新を行う

ベルヌーリ分布とは

ヤコブ・ベルヌーイ　wikipediaより引用 — *ヤコブ・ベルヌーイ　wikipediaより*引用

Bernoulli(ベルヌーリ分布) とはどの様なものでしょうか。

ベルヌーイ分布（英: Bernoulli distribution）とは、数学において、確率 $ $p$$ で $1$ を、確率 $ $q = 1 - p$$ で $0$ をとる、離散確率分布である。
ベルヌーイ分布という名前は、スイスの科学者ヤコブ・ベルヌーイに因んでつけられた名前である。
$$X$$ をベルヌーイ分布に従う確率変数とすれば、
$P(X=1)=p,\qquad P(X=0)=q=1-p$
である。確率変数 $ $X$$ の平均は $ $p$$ , 分散は $ $pq = p (1 - p)$$ である。
ベルヌーイ分布の確率質量関数は次のように表される。
$f(k;p)=p^{k}(1-p)^{1-k}\!\quad {\text{for }}k\in \{0,1\}$ .
$$k$$ は確率変数である。
ベルヌーイ分布は、指数分布族である。

>> Wikipedia 「ベルヌーリ分布」より一部引用

以下がBernouli分布の式となります。

$$\text { Bernoulli}(y | \theta)=\theta^{y}(1-\theta)^{1-y}$$

式について詳しく解説します。

このBernoulli 分布はコインの表や裏、赤玉か青玉など2者択一の場合に使用する確率分布の事です。

$ y $ は0か1の2択を取ります。今回の袋の場合だと青玉を選択するであれば $y$ は0, 赤玉を選択するであれば $y$ は1 という様に設定します。

そして次に、$θ$ の値によって確率分布が決定します。

例えば、赤玉を選ぶのか、青玉を選ぶのかというこの問題設定でも利用する事ができます。

袋A の場合($Y =1$ の場合)だと、赤玉を引く確率を $θ$ とすれば、

$$p(Y=1 | \theta=0.2)=0.2$$

袋B の場合($Y=0$ の場合には、赤玉を引く確率を$θ$ とすれば

$$p(Y=1 | \theta=0.6)=0.6$$

となるわけです。

まとめ|ベイズ更新を例題を用いて学習

今回はベイズ更新を実際に例題を通して学習しました。

また、例題は２者択一の問題であったため、今回はベルヌーリの分布を用いて分布の計算を行いました。

参考になれば幸いです。今回はこれでおわりとします。